卷積在信號處理領(lǐng)域有極其廣泛的應(yīng)用，也有嚴(yán)格的物理和數(shù)學(xué)定義。本文只討論卷積在數(shù)字圖像處理中的應(yīng)用。

在數(shù)字圖像處理中，有一種基本的處理方法:線性濾波。待處理的平面數(shù)字圖像可被看做一個大矩陣，圖像的每個像素對應(yīng)著矩陣的每個元素，假設(shè)我們平面的分辨率是 1024 * 768，那么對應(yīng)的大矩陣的行數(shù)= 1024，列數(shù)=768 。

用于濾波的是一個濾波器小矩陣(也叫卷積核)，濾波器小矩陣一般是個方陣，也就是行數(shù)和列數(shù)相同，比如常見的用于邊緣檢測的 Sobel 算子 就是兩個 3*3 的小矩陣.

進行濾波就是對于大矩陣中的每個像素，計算它周圍像素和濾波器矩陣對應(yīng)位置元素的乘積，然后把結(jié)果相加到一起，最終得到的值就作為該像素的新值，這樣就完成了一次濾波。

上面的處理過程可以參考這個示意圖：

圖像卷積計算示意圖：

對圖像大矩陣和濾波小矩陣對應(yīng)位置元素相乘再求和的操作就叫卷積(Convolution)或協(xié)相關(guān)(Correlation).

協(xié)相關(guān)(Correlation)和卷積(Convolution)很類似，兩者唯一的差別就是卷積在計算前需要翻轉(zhuǎn)卷積核，而協(xié)相關(guān)則不需要翻轉(zhuǎn).

以 Sobel 算子為例

Sobel 算子 也叫 Sobel 濾波, 是兩個 3*3 的矩陣，主要用來計算圖像中某一點在橫向/縱向上的梯度，看了不少網(wǎng)絡(luò)上講解 Sobel 算子 的文章，發(fā)現(xiàn)人們常常把它的橫向梯度矩陣和縱向梯度矩陣混淆。這可能與 Sobel 算子 在它的兩個主要應(yīng)用場景中的不同用法有關(guān)。

Sobel 算子的兩個梯度矩陣: Gx 和 Gy

這里以 Wiki 資料為準(zhǔn)，Sobel 算子 有兩個濾波矩陣：Gx 和 Gy, Gx 用來計算橫向的梯度，Gy 用來計算縱向的梯度， 下圖就是具體的濾波器：

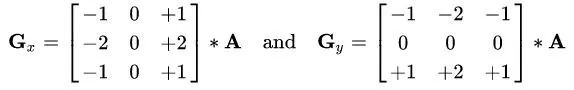
? 注意：這里列出的這兩個梯度矩陣對應(yīng)于橫向從左到右，縱向從上到下的坐標(biāo)軸，也就是這種：

原點 O -------> x軸 | | | V y軸

Sobel 算子的用途

它可以用來對圖像進行邊緣檢測, 或者用來計算某個像素點的法線向量. 這里需要注意的是：

邊緣檢測時：Gx 用于檢測縱向邊緣，Gy 用于檢測橫向邊緣。

計算法線時：Gx 用于計算法線的橫向偏移，Gy 用于計算法線的縱向偏移。

計算展開

假設(shè)待處理圖像的某個像素點周圍的像素如下：

那么用 Gx 計算展開為：

橫向新值 = (-1)*[左上] + (-2)*[左] + (-1)*[左下] + 1*[右上] + 2*[右] + 1*[右下]

用 Gy 計算展開為:

縱向新值 = (-1)*[左上] + (-2)*[上] + (-1)*[右] + 1*[左下] + 2*[下] + 1*[右下]

前面說過，做圖像卷積時需要翻轉(zhuǎn)卷積核，但是我們上面的計算過程沒有顯式翻轉(zhuǎn)，這是因為 Sobel 算子 繞中心元素旋轉(zhuǎn) 180 度后跟原來一樣。不過有些 卷積核 翻轉(zhuǎn)后就變了，下面我們詳細(xì)說明如何翻轉(zhuǎn)卷積核。

卷積核翻轉(zhuǎn)

前面說過, 圖像卷積計算, 需要先翻轉(zhuǎn)卷積核, 也就是繞卷積核中心旋轉(zhuǎn) 180度, 也可以分別沿兩條對角線翻轉(zhuǎn)兩次, 還可以同時翻轉(zhuǎn)行和列, 這3種處理都可以得到同樣的結(jié)果.

對于第一種卷積核翻轉(zhuǎn)方法, 一個簡單的演示方法是把卷積核寫在一張紙上, 用筆尖固定住中心元素, 旋轉(zhuǎn) 180 度, 就看到翻轉(zhuǎn)后的卷積核了.

下面演示后兩種翻轉(zhuǎn)方法, 示例如下：

假設(shè)原始卷積核為：

方法2：沿兩條對角線分別翻轉(zhuǎn)兩次

先沿左下角到右上角的對角線翻轉(zhuǎn), 也就是 a和i, b和f, d和h交換位置, 結(jié)果為：

再沿左上角到右下角的對角線翻轉(zhuǎn)，最終用于計算的卷積核為：

方法3：同時翻轉(zhuǎn)行和列

在 Wiki 中對這種翻轉(zhuǎn)的描述：

convolution is the process of flipping both the rows and columns of the kernel and then multiplying locationally similar entries and summing.

也是把卷積核的行列同時翻轉(zhuǎn)，我們可以先翻轉(zhuǎn)行，把 a b c跟 g h i 互換位置, 結(jié)果為：

再翻轉(zhuǎn)列, 把 g d a 和 i f c 互換位置，結(jié)果為：

在 Wiki 中有一個計算展開式，也說明了這種翻轉(zhuǎn)：

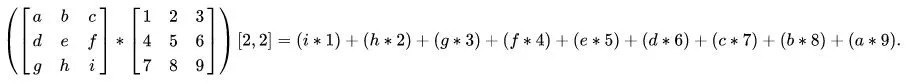
? 注意：這里要跟矩陣乘法區(qū)分開，這里只是借用了矩陣符號，實際做的是對應(yīng)項相乘，再求和。

圖像邊緣像素的處理

以上都默認(rèn)待處理的像素點周圍都有像素，但是實際上圖像邊緣的像素點周圍的像素就不完整，比如頂部的像素在它上方就沒有像素點了，而圖像的四個角的像素點的相鄰像素更少，我們以一個圖像矩陣為例：

位于左上角的像素點的周圍就只有右側(cè)和下方有相鄰像素，遇到這種情況，就需要補全它所缺少的相鄰像素，具體補全方法請參考下一節(jié)的代碼。

用GPU進行圖像卷積

如果在 CPU 上實現(xiàn)圖像卷積算法需要進行4重循環(huán)，效率比較差，所以我們試著把這些卷積計算放到 GPU 上，用 shader 實現(xiàn)，結(jié)果發(fā)現(xiàn)性能相當(dāng)好，而且因為頂點著色器和片段著色器本質(zhì)就是一個循環(huán)結(jié)構(gòu)，我們甚至不需要顯式的循環(huán)，代碼也清晰了很多。

圖像卷積在代碼中的實際應(yīng)用，下面是一個 GLSL 形式的著色器，它可以根據(jù)紋理貼圖生成對應(yīng)的法線圖：