引言

作為信息采集和數據處理的關鍵組成部分，無線傳感器網絡（ wireless sensor networks,WSNs） 也得到了快速發展。WSNs 是集無線通信技術、傳感器技術、嵌入式計算技術、信息處理技術、組網技術等現代網絡技術于一體的網絡，突出優點是能在惡劣環境下實現無線的信息采集和處理，具有非常廣的應用前景。節點的位置信息是WSNs實現應用的重要一環，目前，針對節點定位的研究中有很多很成熟的算法，依據是不是需要測距，主要分為基于測距算法（ range-based） ,典型的有cooperative ranging 算法、NHopmultilateration primitive 算法、Euclidean等，無需測距算法，典型的有DV-Hop 算法、Amorphous 算法、APIT算法、Bounding Box 算法、Centroid 算法等。

由于WSNs 的節點非常多，雖然測距算法有很好的精度保證，但節點必須攜帶額外的測距設備，這樣會很大程度上增加定位成本，而無需測距盡管不如測距那樣準確，但在很多應用場合能達到需要的精度，而且在功耗等方面有較大的優勢。本文選取無需測距算法中典型的4 個算法，包括Amorphous 算法、APIT 算法、Bounding Box 算法、Centroid算法，分別給出在不同參數條件下的仿真定位效果，以便于技術人員在不同條件下選取最優的算法。

1 無需測距算法原理

1. 1 Amorphous 算法

Amorphous 算法是由麻省理工大學的Nagpal R 等人提出的，其主要思想就是把錨節點和未知節點的跳數以及平均每跳距離的乘積作為兩者之間的距離，共分三步： 1） 根據距離矢量交換協議，使網絡中的每個節點都獲得到錨節點的最小跳數； 2） 平均每跳距離用節點的通信半徑表示，未知節點計算到每個錨節點的距離； 3） 利用最大似然估計或者三角測量法估計未知節點的位置。

1. 2 APIT 算法

APIT 算法基本思路是，未知節點首先收集鄰近錨節點的信息。假設其周圍有n 個錨節點能與未知節點通信，然后未知節點任意選取其中的3 個錨節點，這樣就確定C3n個三角形。之后利用PIT 測試法逐一判斷未知節點是否在這些三角形中，最后計算包含未知節點的那些三角形重疊區域，把該重疊區域的質心作為未知節點的位置。

1. 3 Bounding Box 算法

Bounding Box 算法是由美國加州大學伯克利分校Semic S N 等人提出的，該算法與APIT 的算法有相似之處，也是計算包含未知節點的重疊區域。只不過該算法定義一種離散的通信模型，這里假定節點的通信范圍是以2 倍的通信半徑為變長，以自身為中心的正方形。如果未知節點周圍有m 個錨節點能與其通信，則計算這些錨節點所組成的正方形重疊區域，以該重疊區域的中心作為未知節點的位置。

1. 4 Centroid 算法

Centroid 算法基本思想是，網絡約定一個定位時間，在該時間段內，錨節點向未知節點發送包含自身未知信息的數據包。未知節點記錄下從每個錨節點的發來的數據包數目，等到定位時間結束后，未知節點計算與錨節點的通信成功率。根據預先設定的閥值，選出那些通信成功的錨節點，最后把這些錨節點的質心作為未知節點的坐標。

2 算法仿真比較

本文給出了以上述4 種無需測距定位算法在不同參數下的仿真結果比較，通過分析這些結果，結合實際情況可以選擇最優的定位算法。

本文分別從定位誤差和定位精度2 個方面考慮，模擬200 m × 200 m 的區域，節點的部署都采用隨機撒播的方式。

本文平均定位誤差定義為估計位置到真實位置的歐式距離與通信半徑的比值。定位比例定義為除錨節點之外成功定位的節點數和未知節點的總數的比值。使用Matlab 仿真軟件。

1） 假定區域有150 個節點，包括錨節點和未知節點，采用散亂撒播的方式。無線傳感器的節點的能量有限，通信半徑一般在幾十米左右、不失一般性，這里假定通信半徑為30 m,把錨節點的比例作為變量，給出比較仿真結果如圖1、圖2 所示。

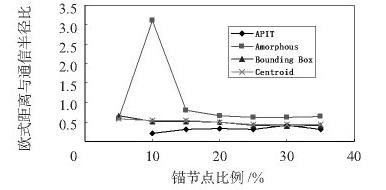
圖1 散亂布置條件下平均定位誤差隨錨節點比例變化趨勢圖

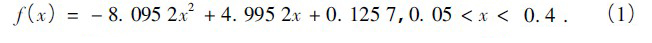
圖2 散亂布置條件下定位比例隨錨節點比例變化趨勢圖

2） 和第一部分參數設置相同，但這里固定錨節點比例為10 %,考察定位誤差和定位比例隨通信距離變化情況，仿真結果如圖3、圖4 所示。

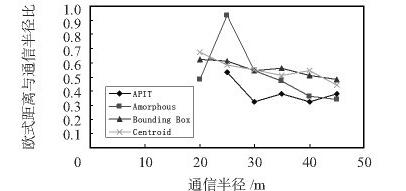
圖3 散亂布置條件下平均定位誤差隨通信半徑變化趨勢圖

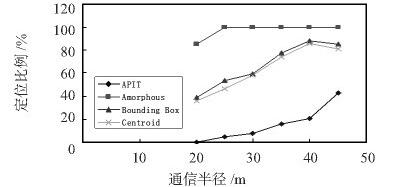
圖4 散亂布置條件下定位比例隨通信半徑變化趨勢圖

3） 采用規則部署的方式，即把這部分區域采用網格法劃分成一個個規則的小正方形區域，每個節點部署隨機部署在小正方形邊上。為了和第一，二部分相似，這里設置小正方形邊長為17 m,那么，總節點數大約為144 個，錨節點和未知節點的部署仍采用隨機撒播方式。這里假定通信半徑為30 m,考察定位誤差和定位比例隨錨節點比例變化情況，仿真結果如圖5、圖6 所示。

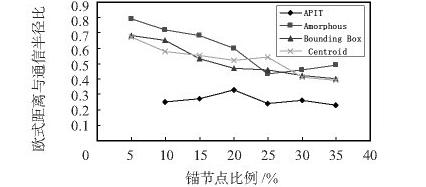
圖5 規則部署條件下平均定位誤差隨錨節點比例變化趨勢圖

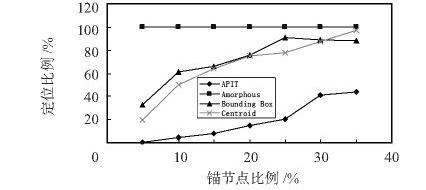
圖6 規則部署條件下定位比例隨錨節點比例變化趨勢圖

4） 參數和第三部分相同，只是這里固定錨節點比例為15 %,因為在這一部分錨節點比例為10 % 時仿真顯示有些算法的定位效果不太明顯，不易對比。考察定位誤差和定位比例隨隨通信半徑變化趨勢，仿真結果如圖7、圖8 所示。

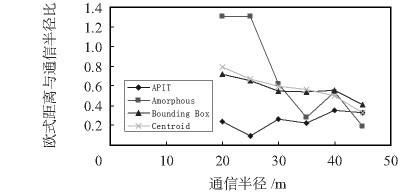
圖7 規則部署條件下平均定位誤差隨通信半徑變化趨勢圖

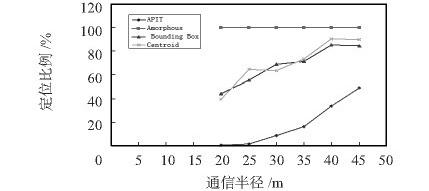
圖8 規則部署條件下定位比例隨通信半徑變化趨勢圖

通過這些仿真圖，可以很方便地查找適合需要的定位算法。

例如： 對某一區域進行定位，屬于隨機散亂部署情況，要求定位精度不是很高但要穩定，但是定位比例要求要大，最重要成本要求很小，只是簡單的測試，而且要求能長時間工作。在這種要求情況下，考察圖1 ~ 圖4.注意到隨機散亂部署的情況下，Amorphous 算法雖然定位比例幾乎為100 %,但誤差大，且有很大跳躍性，排除。APIT 算法雖然定位精度最高，但定位的比例隨錨節點變化非常明顯，這顯然會需要很多錨節點，這樣會很大程度上增加成本，排除。

WSNs 節點的通信半徑會隨著發射功率減少而減少，為了能長時間工作，要求網絡能在通信距離較小時也能準確定位。

Bounding Box 算法和Centroid 算法2 種算法，定位效果隨通信半徑變化的趨勢（ 圖3、圖4） 基本吻合，而且2 種算法的定位誤差在通信半徑相同時，變化趨勢（ 圖1） 基本相同，但注意到圖2,在錨節點比例相同情況，而且在錨節點比例較小區域（ 20%以下） ,Bounding Box 算法比Centroid 算法有更高的定位比例，所以，最終選擇Bounding Box 算法。然后根據實際具體的參數部署節點，在定位算法上選擇BoundingBox 算法即可。

使用Matlab 軟件給出一個具體的函數，例如： 對圖6 中Bounding Box 算法的變化趨勢圖，利用Matlab 曲線擬合函數，測試結果如圖9 所示。

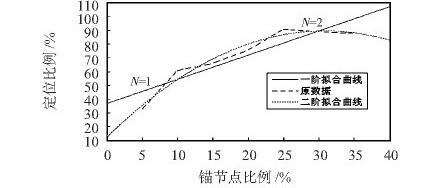
圖9 數據擬合曲線圖

可以發現N = 2 階的擬合曲線和原曲線比較接近，故采用N = 2 階曲線擬合函數，根據Matlab 的計算結果，有：

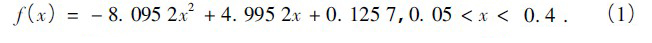
確定這樣一個函數后就可以根據實際具體的需要值代入就可以計算出定位的效果。其他的算法在不同參數條件下利用這種方法確定一個函數，進而計算出定位效果。

這里分別考慮散亂部署和規則部署2 種情況，對于每一種情況，f（ x） ,g（ x） 表示擬合定位誤差函數和擬合定位比例函數，x i（ i = 1,2,3,4） 分別表示APIT 算法，Amorphous算法，Bounding Box 算法，Centroid 算法錨節點比例，y i = 1,2,3,4分別表示以上4 種算法的通信半徑，wi,w2分別表示考慮定位誤差和定位比例的權重，定義定位效果Ci,這樣有：

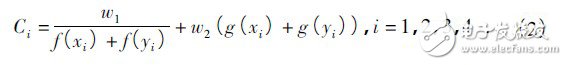
根據實際給出的成本參數轉換為錨節點的比例，再根據實際要求的工作時間長短換算成一定通信半徑，代入上式就可以求出定位效果，最后有：

根據式（ 3） 求出定位效果中取得最大值的算法，這樣就確定哪種算法最優了。

3 結束語

本文給出了無需測距算法中典型的4 種定位算法，給出了它們分別在不同參數下的仿真定位效果，對工程人員選擇適合的算法提供了很好借鑒，在此基礎上，本文提出了一種基于數據擬合方法的定位效果逼近函數，并根據這些函數給出了具體的計算公式，這樣就能根據實際要求，轉換為某范圍或某具體值代入計算公式就可以確定哪種算法最優了。