1 差分跳頻
相關差分跳頻(DFH)通信是近年出現的跳頻通信方式。美國Sanders公司研制的相關跳頻增強擴譜CHESS電臺就采用這種差分跳頻技術,實現了在短波波段5 000跳/秒的跳頻速率和最高19.2 kbit·s-1的數傳速率。
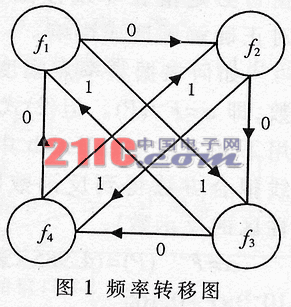
差分眺頻的基本原理:當前時刻的工作頻率fn由上一跳的工作頻率fn-1和當前時刻的信息符號Dn決定,即
fn=G(fn-1,Dn)
其中,G(fn-1,Dn)是一個特定函數,文中稱為G函數,它決定了差分跳頻的數據/頻率映射關系。由此可見,相鄰跳變頻率之間通過數據序列建立了一定的相關性,亦即相鄰頻率的相關性攜帶了待發送的數據信息,因此這種跳頻方式也被稱為相關差分跳頻。
2 差分跳頻技術的特點
差分跳頻技術集跳頻圖案、信息調制與解調等功能于一體,構成與傳統跳頻技術完全不同的技術體制,它具有以下特點:
(1)差分跳頻體制是一種相關跳頻體制,差分跳頻通過G函數變換,使相鄰或多跳頻率之間具有相關性,其相關性攜帶了待發送的數據信息,收端也是根據其相關性還原數據信息,所以也將這種跳頻體制稱為相關跳頻。在常規跳頻體制中,時間上相鄰的頻率與其傳輸的數據信息無關。
(2)差分跳頻體制是一種異步跳頻體制,差分跳頻的收端無法預知每個時刻的發端頻率,在工作帶寬內進行寬帶數字化接收,接收端不需要頻率合成器,從這個意義上說,差分跳頻是一種異步跳頻。
(3)G函數具備數據的調制解調功能,差分跳頻無需傳統定頻或跳頻體制中的基帶和中頻調制,發端經G函數變換,實現數據與頻率之間的"數/頻"編碼,收端先對接收到的直接攜帶信息的射頻頻率進行有效檢測,再經過G函數的逆變換即可恢復出數據信息,實際這也是一種調制解調過程。相同的情況,這是差分跳頻圖案產生的機理決定的,普通跳頻一般不具備這個特點。
(4)跳頻圖案沒有實時時間參與運算在傳統跳頻圖案產生過程中,除跳頻時序控制以外,原始跳頻密鑰Pk和時間參數TOD參與跳頻圖案運算。而在差分跳頻圖案的產生過程中,數據流參與跳頻圖案的運算,相當于跳頻密鑰,與實時時間TOD無關。數據流對跳頻通信的接收端是未知的。
由于差分跳頻與傳統跳頻的原理有很大差別,造成其組網性能也有很大不同。例如,傳統跳頻電臺組網時,相同頻率造成頻率碰撞,形成多址干擾,而頻率不同時,不構成多址干擾;對于差分跳頻電臺,不同頻率可能會造成接收方數據的誤判,從而形成多址十擾;頻率相同時,如果削弱有效頻率的幅度,則形成多址干擾,如果加強頻率的幅度,則不形成多址干擾,與兩個頻率之間的相位有關。
傳統的同步組網是指,各跳頻網在技術體制、跳頻圖案算法及跳頻密鑰相同以及同一張頻率表的條件下,各跳頻網每一跳的起跳時刻相同,并且任一時刻的各網瞬時頻率正交。由于傳統的同步組網是同頻造成多址干擾,而差分跳頻則是異頻可能會形成多址干擾。因此差分跳頻同步組網的概念應擴展為在同一張頻率表的條件下,各跳頻網每一跳的起跳時刻相同時,任一時刻各網瞬時頻率不相互形成干擾。差分跳頻圖案是由隨機數據信息控制G函數產生的,而每部電臺和各跳頻網的數據源是不同的,是相互獨立的,相互之間不可能有某種約束關系,導致了即使各臺及各網之間在時間上有約束關系,也難以實現各臺各網之間頻率的人工干預,這樣一來,當接收方收到的頻率為當前G函數映射出的除當前發送頻率之外的m-1個頻率中的某一個頻點時,就會形成多址干擾。也就是說,要做到差分跳頻各網當前跳變頻率不落在其余網G函數映射的頻率子集之內相當困難。需要通過研究G函數的算法,尋找適當的映射途徑,使得各網跳變時刻相同,但任一時刻各網瞬時頻率不相互形成多址干擾。
3 AWGN下差分跳頻系統的多用戶能力分析
圖1為DFH多用戶系統模型。每個發射機提供一種交織編碼樣式,這種編碼的碼型同數據比特流一起構成傳輸波形。在每個接收機處,解碼器也使用與對應用戶相同的碼型。如果某接收機對多個發送信號感興趣,它為合成信號中每個發送信號創建一種檢測交織編碼樣式。其他的發送信號則被認為是干擾,而DFH解碼算法能很好地抑制這些干擾。然而某些時候,在已經投入使用的DFH多用戶系統中,用戶數量會影響解碼的性能,而且對干擾的消減程度也是適當的。

圖1 DFH多用戶系統示例
根據頻率數、信噪比、產生一個DFH多用戶系統的理論上的誤碼率γ,以及干擾的數量N-1,并使用多用戶信干比SINR為γMU。
在DFH解碼的每一階段,干擾信號會造成模糊概率ρ=(2b-1)/M.換句話說,來自功率為S某一干擾信號的有效的干擾為ps=(2b-1)S/M.因此,如果存在N個功率相等的用戶,每個用戶都以與無干擾狀態下的信噪比γ=S0/N相一致的信號電平來進行傳送,這樣就可以確定有效的信干比
γMU=γ/(1+γ(2b-1)(N-1)/M) (1)
這樣就可以得到高斯白噪聲信道條件下的總用戶數為N的DFH多用戶系統的理論誤碼率為
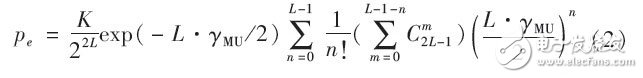
在用戶數N=10,b=1的情況下,仿真信噪比隨跳頻頻率個數的變化如圖2所示。
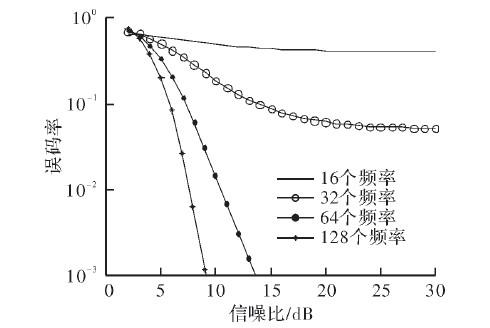
圖2 M值不同的條件下DFH系統誤碼率隨信噪比的變化
在圖2中,畫出了用戶數為N=10,M=16、M=32、M=64、M=128的條件下,誤碼率隨信噪比的變化曲線。由圖可以看出,可用頻點數M越高,誤碼率隨信噪比的變化越快,且M越大,相應信噪比條件下的誤碼率越小,系統性能越好。
設定仿真參數,跳頻頻率個數M=64,b=1,用戶數以2的指數增加,仿真如圖3所示。
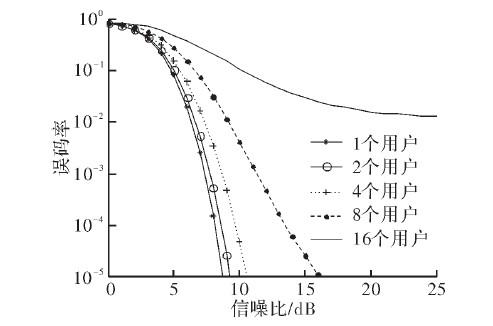
圖3 DFH系統在用戶數不同的情況下的誤碼率比較
在圖3,中使用Matlab分別畫出了用戶數N=1、N=2、N=4、N=8、N=16時,DFH系統誤碼率隨信噪比的變化圖。由圖可以看出,用戶越多,DFH系統的誤碼率越大,信噪比曲線越平緩,即誤碼率隨信噪比變化的速度較慢;用戶越少誤碼率越小,信噪比曲線就越陡峭,即誤碼率隨信噪比變化的速度較快;此外,系統用戶數越少,在相應信噪比條件下誤碼率越小,說明干擾小。
4 結束語
討論了差分跳頻系統的多用戶能力,并進行了仿真計算,得出了有益的結論,這將對差分跳頻新體制進入實用化有一定的指導意義,為差分跳頻組網問題提供了有益的參考,但差分跳頻系統的多用戶能力還有待于進一步研究,可將其與其他跳頻技術的組網能力進行比較研究。
-
解碼器
+關注
關注
9文章
1161瀏覽量
41527 -
頻率合成器
+關注
關注
5文章
229瀏覽量
32645 -
仿真
+關注
關注
51文章
4202瀏覽量
135000
發布評論請先 登錄
相關推薦
多用戶檢測技術
TH-PPWM在多用戶環境下的性能分析
多用戶檢測技術在WCDMA中的應用
基于DSP的多用戶混沌保密通信系統研究
多用戶信號分離與干擾抑制算法







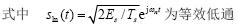












評論