引言

數字濾波器作為語音與圖象處理、模式識別、雷達信號處理、頻譜分析等應用中最基本的處理部件，現已成為最常用的工具之一。它既能滿足濾波器對幅度和相位特性的嚴格要求，又能避免模擬濾波器所無法克服的電壓漂移、溫度漂移和噪聲等問題。而對于具有線性相位特性的濾波問題，設計時一般都選擇FIR濾波器。

相對于窗函數法和頻率設計法，在將理想頻率響應和實際頻率響應之間的加權逼近誤差均勻地分散到濾波器的整個通帶和阻帶最小化和最大誤差這個意義上來說，Chebyshev逼近法可以被視為最佳的設計準則。

1設計原理

1.1 FIR數字濾波器

對于長度為N、輸入為x(n)、輸出為y(n)的FIR濾波器，其輸出函數可用差分方程表示為：

事實上，具有線性相位的濾波器都具有對稱性或反對稱性，即單位樣本響應可滿足條件：

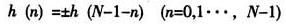
1.2 Chebyshev逼近法

(1)線性相位FIR濾波器的四種情況

根據單位樣本響應的對稱性或反對稱性，以及濾波器長度的奇偶性，其線性相位FIR濾波器有以下四種情形：

情形1：單位樣本響應具有對稱性，即h(n)=h(N-1-n)，且N為奇數；

情形2：單位樣本響應具有對稱性，即h(n)=h(N-1-n)，且N為偶數；

情形3：單位樣本響應具有反對稱性，即h(n)=-h(N-1-n)，且N為奇數；

情形4：單位樣本響應具有反對稱性，即h(n)=-h(N-1-h)，且N為偶數。

(2)誤差函數E(ω)

若定義實值理想頻率響應Hd(ω)在通帶內為1，在阻帶內為0；同時定義加權函數W(ω)在通帶內為δ2／δ1(δ1為通帶波紋，δ1為阻帶波紋)，阻帶內為1。則可將加權逼近誤差E(ω)定義為：

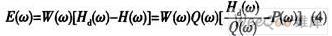
如誤差函數已知，則Chebyshev逼近只需確定濾波器參數{α(k)}，然后使其逼近頻帶E(ω)上的最大絕對值最小化。即要找到下式的解：

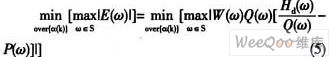
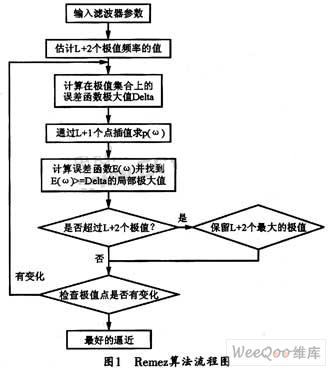
該問題的解法已由Parks和McClellan解決，稱之為Remez交換算法。該算法是建立在交錯定理的基礎上的。圖1所示是Remez算法的流程圖。

(3)交錯定理

2 FIR數字濾波器在ARM上的實現

Chebyshev逼近法主要利用Remez交換算法來實現，其設計流程圖如圖1所示。本文主要討論怎樣在ARM平臺上實現該算法，從而設計FIR數字濾波器。其具體設計流程圖如圖2所示，步驟如下：

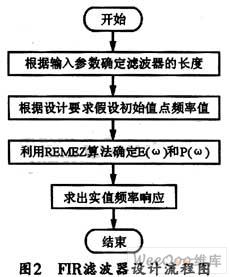
求出P(ωk)的值。事實上，也可以利用關于P(ω)的Lagrange差值公式來求解P(ω)，具體公式為：

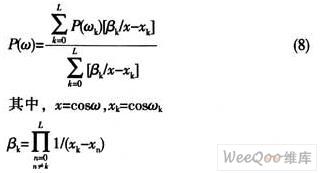
(5)誤差E(ω)的計算

有了上面的基礎，再利用公式(4)就可以求出E(ω)，然后重復上述過程，直到找到符合要求的E(ω)為止，這樣，就可以確定P(ω)的值。

(6)實值頻率響應H(ω)的確定

通過P(ω)得到最佳解后，便可直接利用公式(3)來確定實值頻率響應，而不必再去求解參數{αk}。

3結束語

本文在Chebyshev逼近法的基礎上，提出了一種基于ARM平臺的數字濾波器的軟件實現方法。實驗結果表明，利用此方法切實可行并能達到要求，并可初步用于實際的信號處理，為進一步實用化打下良好的基礎。