自控網系統（cyber net system）又稱自修正系統（self-modifying system），簡稱自控系統。它是Petri網中的一類，與P/T系統區別僅僅在于有向弧的權受庫所控制，它的關聯矩陣含變量元素，而P/T系統的關聯矩陣是常量，因此，P/T系統是線性的，而自控系統是非線性的，P/T系統只是自控網系統的一種特殊情況。雖然自控系統在上世紀70年代初就已被提出，但由于自控系統的非線性關系，無法直接套用其它網系統的分析技術，對自控系統的研究成果并不多。而正由于自控系統的非線性關系，它有更強的描述能力和更復雜的性質。因此，對自控系統的研究具有重要意義。北京大學袁崇義教授對自控系統進行了深入的研究，提出了自控系統的S-不變量和T-不變量的定義及其計算。本文采用EDA工具，用在系統可編程邏輯器件來實現自控系統，并通過仿真對自控系統進行分析。其目的是擴大自控系統的應用范圍，激起人們對自控系統研究的興趣。

1．自控系統簡介

定義1 ?=（S，T；F，W，M0）為自控系統的條件是：

（1） （S，T；F）為有向網，稱為?的基網。

（2） W：S?T?T?S→{0，1，2，…}?S，且W（x，y）≠0當且僅當W（x，y）?F，稱為?的權函數。

（3） M0：S→{0，1，2，…}為?的標識。

自控系統與P/T系統區別在于權函數W的值域中增加了S。定義中假定了每個S_元的容量是無限的，但在硬件實現時，由于存儲器的位數有限，S_元的容量都是有限的，但這不影響對問題的研究。

定義2

（1） 映射M：S→{0，1，2，…}稱為?的標識。

（2） 標識M下的權函數WM定義為：?（x，y）?S?T?T?S，

（3） 變遷t?T在標識M有發生權（即M［t》）的條件是：?s?S：M（s）≥WM（s，t）且有s??t使WM（s，t）》0，即t至少有一個非0的輸入權。

（4） 若M［t》，則t可以發生，后繼標識M’由下式給出：

M’=M（s）+WM（t，s）-WM（s，t）后繼關系記做M［t》M’。

定義2給出了自控系統的變遷規則。顯然，變遷發生方式對最終標識的影響很大。P/T系統中“并發能到達的標識，順序也能到達”，而這在自控系統中不成立。自控系統的動態演變是以T上的多重集的并發一步一步演變。

文給出了Fibonacci數列的增廣Petri網模型，用了19個庫所，18個變遷和大量的抑制弧。圖1是計算Fibonacci數列的自控網系統［2］，十分簡潔，充分反映了自控網系統的建模能力。圖1中，s5、s6中的托肯數M（s5）、M（s6）代表Fibonacci數列中數的位置，相應的Fibonacci數由s3、s4中的托肯數表示。圖示情況下可以看出，數列的第1個數的值為0，第2個數的值為1。s2和s4確保t1和t2順序發生。

圖1 自控網系統

由圖可知，變遷t2有發生權，t2發生后，t1有發生權。設t2、t1發生后的標識分別為M1和M2，根據自控系統的變遷規則計算如下：

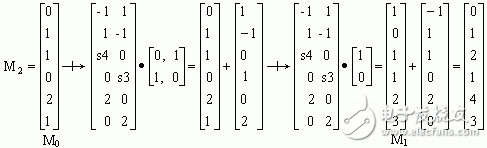
式中運算符號 為替換加，即將向量中的變量先進行替換后再相加。

2．自控網系統的仿真分析與硬件實現

在系統可編程邏輯器件由于結構不同可分為CPLD和FPGA兩種，芯片內部有幾千至幾千萬個標準門，人們通過EDA軟件工具，采用硬件描述語言對系統的行為或邏輯功能進行描述，經編譯、仿真、優化、適配并通過電纜下載到芯片中，從而獲得滿足功能要求的芯片。在系統可編程器件的特點是不要專門的編程器；器件可先焊接在電路板上，然后再對它進行編程，不滿足要求還可重新編程；設計可以在各種層次上進行，可采用自下而上或自上而下的設計方法，受到電子工程師的歡迎，并可在一塊芯片上構造一個復雜的數字系統［4］。

下面以圖1中s2和s3為例說明自控系統的設計方法。

對于s2，t1發生時，它獲得一個托肯，t2發生時，它失去一個托肯，可用一個觸發器來代表它的狀態，觸發器為1時表示它有托肯，觸發器為0時，表明它沒有托肯。S3用8位寄存器表示，當t1發生時，s4中有多少托肯它增加多少托肯。

再來分析一下t1、t2有發生權的條件，t1有發生權的條件是：tt1=（s1= =1）&（s2= =0）&（s5《=13）&（s3《=^h7f）&（s4《=^h7f），其中^h代表16進制，s5、s6分別用4位寄存器表示。t2有發生權的條件是：tt2=（s1= =0）&（s2= =1）&（6《=13）&（s3《=^h7f）&（s4《=^h7f）。由于ABEL-HDL中是無符號數運算，故采用了條件（s3《=^h7f）&（s4《=^h7f），以防s2和s3的存儲器數據溢出。

用set信號置初始標識，采用同步置位，同步信號為clk，上升沿作用。t1和t2加外部同步信號。

程序編制完成后，進行編譯并進行邏輯化簡。可以通過編制測試程序對系統的功能進行仿真。本文是在Lattice公司的EDA軟件工具ispDesign EXPERT環境中對圖1所示自控網系統進行設計和仿真的，仿真波形如圖2所示。從波形圖中可看出，T1的第1個脈沖到來時，由于變遷T1沒有發生權，所以不會發生，數據沒有變化。當計算到第13個Fibonacc數時，s4為144時，為防止數據溢出導致不正確的結果，停止了計算。經適配并最終下載在ispPLSI1032E芯片中，獲得計算Fibonacci級數的專用芯片。

圖2 仿真波形

3．結束語

自控網系統由于它的非線性特點，用它來描述復雜系統特別是一些算法比其它的Petri網子類更有效。用硬件描述語言對自控網系統進行描述，通過EDA軟件工具進行仿真和硬件實現，為自控網系統的性能分析提供了新的途徑，也為它的實際應用提供了物理保證。隨著人們對自控網系統研究的深入，本文所提出的自控網系統的仿真與硬件方法將得到進一步的應用。