前言
我最近一直在公司做檢索性能優(yōu)化。當(dāng)我看到這個算法之前,我也不認(rèn)為我負(fù)責(zé)的檢索系統(tǒng)性能還有改進(jìn)的余地。但是這個算法確實太牛掰了,足足讓服務(wù)性能提高50%,我不得不和大家分享一下。其實前一段時間的博客中也寫到過這個算法,只是沒有細(xì)講,今天我準(zhǔn)備把它單獨拎出來,說道說道。說實話,本人數(shù)學(xué)功底一般,算法證明不是我強(qiáng)項,所以文中的證明只是我在論文作者的基礎(chǔ)上加入了自己的思考方法,并且還沒有完全證明出來,請大家見諒 ! 歡迎愛思考的小伙伴進(jìn)行補(bǔ)充。我只要達(dá)到拋磚引玉的作用,就知足了。
回歸正題,我們的檢索服務(wù)中用到了最小編輯距離算法,這個算法本身是平方量級的時間復(fù)雜度,并且很少人在帖子中提到小于這個復(fù)雜度的算法。但是我無意中發(fā)現(xiàn)了另外一個更牛的算法:列劃分算法,使得這個本就很牛的算法性能直接提高一倍。接下來進(jìn)入正題。
列劃分算法
這個算法比較難理解,出自如下論文:《Theoretical and empirical comparisons of approximate string matching algorithms》。In Proceedings of the 3rd Annual Symposium on Combinatorial Pattern Matching, number 664 in Lecture Notes in Computer Science, pages 175~184. Springer-Verlag, 1992。Author:WI Chang ,J Lampe。所以有必要先給大家普及一些共識。
編輯矩陣最小編輯距離在計算過程中使用動態(tài)規(guī)劃算法計算的那個矩陣,了解這個算法的都懂,我不贅述。但是我們的編輯矩陣有個特點:第一行都是0,這么做的好處是:只要文本串T中的任意一個子序列與模式串P的編輯距離小于某個固定的數(shù)值,就會被發(fā)現(xiàn)。
給大伙一個樣例,文本串T=annealing,模式串P=annual:

注意,第一行都是0,這是與傳統(tǒng)最小編輯距離的最大區(qū)別,其余的動歸方程完全相同。
對角線法則編輯矩陣沿著右下方對角線方向數(shù)值非遞減,并且至多相差1。
行列法則每行每列相鄰兩個數(shù)至多相差1。
觀察編輯距離矩陣,我們發(fā)現(xiàn)如下事實:每一列是由若干段連續(xù)數(shù)字組成。所以我們把編輯矩陣的每一列劃分成若干連續(xù)序列,如下圖所示:

紅色框中就是一個一個的序列,序列內(nèi)部連續(xù)。
序列-δ 定義對于編輯矩陣的每一個元素D[j][i] (j是行,i是列),若 j – D[j][i] = δ,我們就說D[j][i]屬于i列上的 序列-δ,我們還觀察到隨著j增大,j – D[j][i]是非遞減的。如下圖所示:

序列-δ終止位置每個序列都會有起始和終止位置。序列-δ的終止位置為j,如果j是序列-δ的最小橫坐標(biāo),并且滿足D[j+1][i]屬于序列-ε,并且ε>δ(即j+1-D[j+1][i]>δ)。
長度為0的序列我們發(fā)現(xiàn)如果按照如上定義,每一列上δ的值并不一定連續(xù),總是或有或無的缺少一個數(shù)值。所以我們定義長度為0的序列:當(dāng)D[j+1][i] < D[j][i]時,我們就在序列-δ和序列-(δ+2)之間人為插入一個長度為0的序列-(δ+1)。如下圖所示:

所以,我們按照這個定義,就可以對編輯矩陣的每列進(jìn)行一個劃分,劃分的每一段都是一串連續(xù)數(shù)字。
說了這么多,這個定義有什么用呢?假若,我們每次都能根據(jù)前一列的列劃分情況直接推導(dǎo)出后一列的列劃分情況,那么就可以省去好多計算,畢竟每一個劃分中的每一段的數(shù)字都是連續(xù)的,這就暗示我們可以直接用一個常數(shù)時間的加法直接得到某一個編輯矩陣的元素值,而不用使用最小編輯距離的動態(tài)規(guī)劃算法去計算。
接下來的重點來了,我們介紹這個推導(dǎo)公式,請打起十二分精神!我們按照序列-δ長度是否為0來介紹這個推論。由于其中一個推論文字描述太繁瑣,不容易理解,所以我畫了個圖:
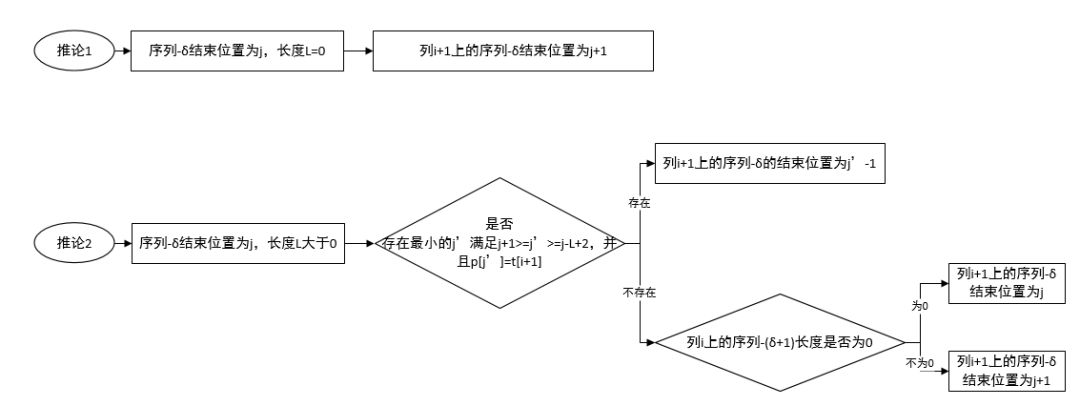
接下來燒腦開始。
推論1:如果列i上長度為0的 序列-δ 的結(jié)束位置為j,則列i+1上的 序列-δ 的結(jié)束位置為 j+1。
證明:由推論前提我們知道 δ = j – D[j][i] + 1 (想想前面說的δ值不連續(xù),我們就人為插入一個中間值,只不過長度為0)。我們觀察編輯矩陣就會發(fā)現(xiàn)如下兩個事實:
事實1:D[j+1][i+1] = D[j][i] ( 別問為什么, 自己觀察, 看看是不是都這樣, 其實可以用反證法,我們就不證明了)。
事實2:D[j+2][i+1] <= D[j][i]。
通過事實1,我們知道D[j+1][i+1]確實屬于 序列-δ,因為 j + 1 – D[j+1][i+1] = j + 1 – D[j][i] = δ。
通過事實2,我們知道列i+1上的序列δ,終止位置為j+1。
所以推論1證明結(jié)束。
推論2: 文字描述略,請看圖
證明:
設(shè)這個序列長度為L,除了每列的第一個序列外,其余序列的其余位置均是當(dāng)前的編輯距離小于等于該列上一個位置的編輯距離:即D[j-L+1][i]<=D[j-L][i],所以,我們可以推出:D[j-L+1][i] <= D[j-L][i];
再根據(jù)編輯矩陣對角線非遞減我們知道,D[j-L+1][i+1] >= D[j-L][i];
綜上兩點我們得到如下大小關(guān)系:D[j-L+1][i+1] >= D[j-L+1][i]。
此外我們知道我們當(dāng)前列的序列-δ截止位置為j,也意味著D[j+1][i] <= D[j][i],同樣根據(jù)對角線法則,我們得出D[j+2][i+1] <= D[j+1][i] + 1 <= D[j][i] + 1。
接下來到了最精彩的一步,我們知道列i當(dāng)前序列-δ內(nèi)的值是連續(xù)的,如果起始編輯距離為A,那么終止編輯距離為A+L-1。
而由我們的推導(dǎo)可以發(fā)現(xiàn):D[j-L+1][i+1] >= A,D[j+2][i+1] <= (A+L-1) + 1 = A+L,而之間跨越的長度為 (j+2)-(j-L+1)+1= L+2。 我們可以推出列i+1上從行j-L+1到行j+2之間的序列一定不連續(xù),否則D[j+2][i+1] >= A+L+2-1= A+L+1,與我們先前的推導(dǎo)矛盾。所以,在j-L+1和j+2之間一定有一個列終止,這樣才能消去一個序號。
此外我們還有一個疑問,列i+1上的序列-δ結(jié)束位置一定在j-L+1和j+1之間么?我們要證明這個事。
證明:
因為δ=j-D[j][i]=j-L+1-D[j-L+1][i]>=j-L+1-D[j-L+1][i+1],即列i+1上的 序列-δ的結(jié)束位置一定在j-L+1或者之后;
由于j+1-D[j+1][i]>δ,根據(jù)對角線法則D[j+2][i+1] <= D[j+1][i]+1,有j+2-D[j+2][i+1]>=j+2-(D[j+1][i]+1)=j+1-D[j+1][i] > δ, 固列i+1上的序列-δ的終止位置一定在j+2之前,即j-L+1到j(luò)+1之間。
后面推論2的分情況討論,我一個也沒證明出來,作者在論文中輕飄飄的一句話“后面很好證明,他就不去證明了”,但是卻消耗了我所有腦細(xì)胞。所以,如果哪位小伙伴把推論2剩下的內(nèi)容證明出來了,歡迎給我留言,我也學(xué)習(xí)學(xué)習(xí)。
這個算法的時間復(fù)雜度是多少呢?作者用啟發(fā)式的方法證明了算法的復(fù)雜度約為$ O(mn/sqrt[2]{b}) $,其中b是字符集大小。
代碼實現(xiàn)
接下來說一下代碼實現(xiàn),給出我總結(jié)出來的步驟,否則很容易踩坑。
編輯矩陣第一列,肯定只有一個序列。
每次遍歷前一列的所有序列,根據(jù)推論1和推論2計算后一列的劃分情況。
如果前一列遍歷完畢,但是下一列還有剩余的元素沒有劃分。沒關(guān)系,下一列剩下的元素都?xì)w為一個新的序列。
預(yù)處理一個表,表中記錄T中的每個字符在P中的位置。可以直接用哈希算法(最好直接ascii碼)進(jìn)行定位,如果位置不唯一,可以拉鏈。進(jìn)行列劃分計算時,從前往后遍歷那一鏈上的位置,直到找到第一個符合條件的,速度出奇的快。盡可能少使用或者不要使用map進(jìn)行定位,測試發(fā)現(xiàn)相當(dāng)慢。
接下來做最不愿意做的事:貼一個代碼,很丑。
inlineintloc(intfind[][200],int*len,intch,intpos){for(inti=0;i=pos)returnfind[ch][i];}return-1;}intnew_column_partition(char*p,char*t){intlen_p=strlen(p);intlen_t=strlen(t);intfind[26][200];intlen[26]={0};intpart[200];//記錄每一個序列的結(jié)束位置//生成loc表,用來快速查詢for(inti=0;i=1if(len[t[i]-'a']>0&&(tmp=loc(find,len,t[i]-'a',b))!=-1&&tmp<=?e)?{??????part[next_cn++]?=?tmp?-?1;????}?else?if(pre_cn?>=2&&part[1]-part[0]!=0){part[next_cn++]=part[0]+1;}else{part[next_cn++]=part[0];}//每列第一個partition尾值tmp_value=part[0];//遍歷前一列剩下的partitionfor(intj=1;j0&&(tmp=loc(find,len,t[i]-'a',b))!=-1&&tmp<=?e)?{??????????part[next_cn++]?=?tmp?-?1;????????}?else?if(j?+?1?
結(jié)語
這個算法應(yīng)用到線上之后,效果非常明顯,如下對比。
優(yōu)化前CPU:
優(yōu)化后CPU:
能力有限,證明不充分,有興趣的小伙伴可以直接去看原版論文,歡迎交流,共同進(jìn)步。
-
算法
+關(guān)注
關(guān)注
23文章
4607瀏覽量
92840 -
數(shù)值
+關(guān)注
關(guān)注
0文章
80瀏覽量
14359
原文標(biāo)題:死磕一周算法,我讓服務(wù)性能提高 50%
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
福音:日本電池新技術(shù)師電池能量密度提高一倍
一種新的基于晶體管級的電路劃分算法
日立將錳類正極材料的產(chǎn)業(yè)用鋰離子電池壽命提高一倍
基于PSO的粗顆粒度可重構(gòu)處理器時域劃分算法設(shè)計劉勰
基于局部模塊度的社團(tuán)劃分算法
ARM Cortex-R8使SoC的性能提高一倍
特許半導(dǎo)體的目標(biāo)是在兩年內(nèi)將其代工能力提高一倍
AirPods Pro耳機(jī)火爆 蘋果要求制造商產(chǎn)量提高一倍
LG化學(xué)計劃將中國的產(chǎn)量提高一倍以上
LG化學(xué)或?qū)⒅袊姵禺a(chǎn)能提高一倍以上
長江存儲或?qū)?021年存儲芯片產(chǎn)量提高一倍
基于狄利克雷問題的動態(tài)劃分算法
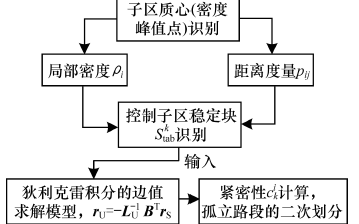
基于節(jié)點多屬性相似性聚類的社團(tuán)劃分算法SM-CD





 列劃分算法,使得這個本就很牛的算法性能直接提高一倍
列劃分算法,使得這個本就很牛的算法性能直接提高一倍











評論