編者按：數據科學家Jonny Brooks-Bartlett撰寫的零基礎概率論教程的第六篇，深入淺出地講解概率分布這一概念。

在之前的文章中，我介紹了概率論的基本概念和基本公理。數學家會為這些感到興奮，但在實踐中，概率論中比較常用的是概率分布。

概率分布用于許多領域，但我們很少看到相應的解釋。通常作者會假定讀者已經了解概率分布了。本文將嘗試解釋什么是概率分布。

什么是概率分布？

回憶一下，隨機變量是值為一個隨機事件的結果的變量（如果不知所云，請溫習下本系列的第一篇）。例如，擲骰子的點數或拋硬幣的結果是隨機變量。

概率分布是隨機變量所有可能結果及其相應概率的列表。

例如，均勻6面骰的概率分布為：

更明確地說，這是一個有限支持的離散單元概率分布的例子。這讀起來比較拗口，所以讓我分解這一表述，逐步理解。

離散（discrete）這意味著如果我選擇任意兩個連續的結果，我無法取得位于兩者之間的結果。例如，考慮投擲六面骰的結果1點和2點，我沒法得到兩者之間的點數（例如，我沒法擲出1.5點）。在數學上，我們會說，結果列表是可數的（不過我不會進一步定義可數集和不可數集了，否則就沒完沒了了）。你大概可以猜想，當我們涉及連續（continuous）概率分布時，這一點會不成立。

單元（univariate）這意味著我們只有一個（隨機）變量。在這一情形下，我們只有擲骰的結果。相反，如果我們有不止一個變量，那我們稱其為多元分布（multivariate distribution）。如果我們有兩個變量，那么這一多元分布的特例稱為二元分布（bivariate distribution）。

有限支持（finite support）這意味著結果的數目是有限的。基本上，支持是定義概率分布的結果。所以，在我們的例子中，支持是1、2、3、4、5、6. 由于這些值不是無限的，所以我們說這是有限支持的概率分布。

函數入門

我們為何談論函數？

在上面的投擲六面骰的例子中，只有六種可能的結果，所以我們可以在一個表格中寫下整個概率分布。但在很多場景中，結果的數量可能很大，用表格羅列會很枯燥乏味。更糟的是，可能結果的數目也許是無限的，在那樣的情形下，就沒法編寫表格了。

為了免去為每個分布編寫表格的麻煩，我們可以轉而定義一個函數。函數允許我們簡潔地定義一個概率分布。

所以，讓我們首先介紹一般意義上的函數，接著再介紹用于概率分布的函數。

什么是函數？

從一個非常抽象的層次上說，函數是一個接受輸入并返回輸出的盒子。在大多數情況下，函數事實上需要對輸入進行一些處理，以得到有用的輸出。

讓我們自行定義一個函數。比方說，這個函數接受一個數字作為輸入，在輸入數字上加2，并返回新數字作為輸出，如下圖所示：

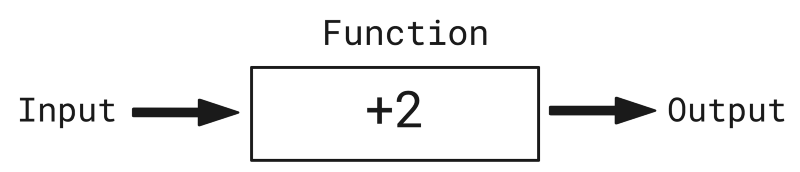
所以，如果輸入是5，我們的函數會加上2，并返回輸出5 + 2 = 7

函數記法

給我們想要創建的所有函數畫示意圖是件枯燥乏味的工作。我們轉而使用符號/字母，以便更簡潔地表示函數。我們用“x”替換單詞“input”（輸入），用“f”替換單詞“function”（函數），用“f(x)”替換單詞“輸出”。所以，上面的示意圖現在變成這樣了：

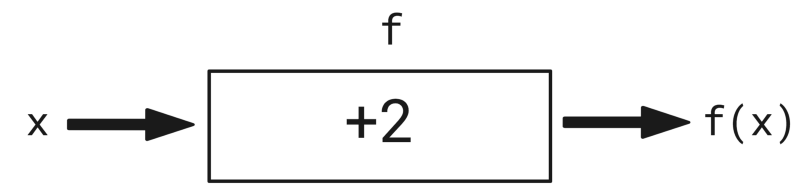
這要好一點，不過，需要畫示意圖表示函數做了什么這個問題仍然存在。數學家可不想浪費寶貴的精力畫盒子，所以發明了更好的表示函數的方式，什么也不用畫。在數學上，我們的函數可以定義為：

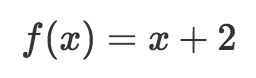
這和上面的示意圖是等價的，因為我們可以明確看到函數的輸入是x，我們的函數稱為f，并且我們知道函數在輸入上加2，并返回x + 2作為輸出。

值得注意的是，函數名和輸入的字母選擇是任意的。我可以說輸入是“a”，將函數稱為“add_two”（加二）：

這和之前的函數定義完全等價。

這里關鍵的一點是，有了函數定義，我們可以看到如何轉換任何輸入。給定函數f(x) = x + 2，我們會知道如果輸入是10做什么，或者如果輸入是10000做什么。所以我們不用像之前那樣列出一個表格。

這里需要指出的是，我們即將使用的函數的輸入和輸出都是數字。然而，函數可以接受任何你喜歡的東西作為輸入，并輸出任何你喜歡的東西（甚至什么都不輸出）。例如，我們可以在編程語言中編寫一個函數，接受一個文本字符串作為輸入，并輸出字符串的第一個字母。下面是用Python編程語言寫的一個例子：

def get_first_letter(my_string):

return my_string[0]

get_first_letter('Hello World') # 結果為 'H'

譯者注：這里僅為示例，實際定義函數的時候還需要考慮輸入字符串為空的情況，需要捕獲IndexError異常或先行判斷字符串是否為空。

用圖像表示函數

函數的主要優勢之一是讓我們知道如何轉換任何輸入，所以我們可以利用這一知識可視化函數。回到之前的例子f(x) = x + 2. 它的圖像是這樣的：

底下的橫軸表示輸入數字，相應地，左側的縱軸表示輸出值f(x) = x + 2. 例如，我們看到，表示函數的藍線穿過了x = 1處的（白色）縱線和f(x) = 3處的（白色）橫線。這從圖像上顯示了f(1) = 1 + 2 = 3.

函數的參數

函數最重要的特征之一是參數。參數是函數內部不必作為輸入傳入的數字。在我們的例子f(x) = x + 2中，數字“2”是一個參數，因為我們需要它來定義函數，但沒有將它納入函數的輸入。

參數之所以重要，是因為它們直接決定輸出。例如，定義另一個函數h(x) = x + 3. 函數f(x) = x + 2和新定義的函數h(x) = x + 3之間唯一的區別是參數值（新函數的參數是“3”而不是“2”）。這一差異意味著相同輸入得到的輸出完全不同。讓我們看下相應的圖像：

參數可以算是概率（分布）函數最重要的特征了，因為它們定義了函數的輸出，告訴我們隨機過程得到特定結果的似然。在數據科學問題中，我們常常試圖估計參數，我之前曾經介紹過兩種估計參數的方法：最大似然估計和貝葉斯推斷。

現在我們可以用函數語言討論概率分布了。

概率質量函數：離散概率分布

當我們使用概率函數描述離散概率分布時，我們將其稱為概率質量函數（probability mass function），通常縮寫為pmf.

還記得我們在這個系列的第一篇提到的隨機變量概率的記法嗎？我們將隨機變量記為大寫的X，而將變量的值記為小寫的x，隨機變量概率則記為P(X=x). 因此，如果我們的隨機變量是投擲骰子的點數，我們可以將擲出3點的概率記為P(X=3) = 1/6.

概率質量函數（記為“f”）返回結果的概率：

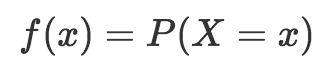
我知道這里開始有點嚇人，但請多容忍一點數學。上面的公式不過是表明，概率質量函數“f”返回結果x的概率。

所以讓我們回到均勻6面骰的例子（你大概已經厭煩這個例子了吧？）。概率質量函數f不過是返回結果的概率。因此擲出三點的概率是f(3) = 1/6.

由于概率質量函數返回概率，所以它必須遵循我在前一篇描述的概率法則（公理）。也就是說，概率質量函數輸出0到1之間的值（含），而所有結果的概率質量函數輸出之和等于1. 在數學上，我們可以將這兩個條件表達為：

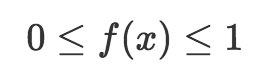
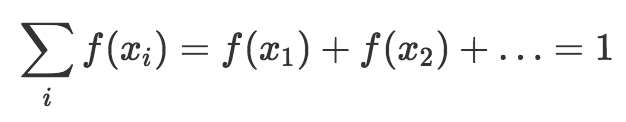
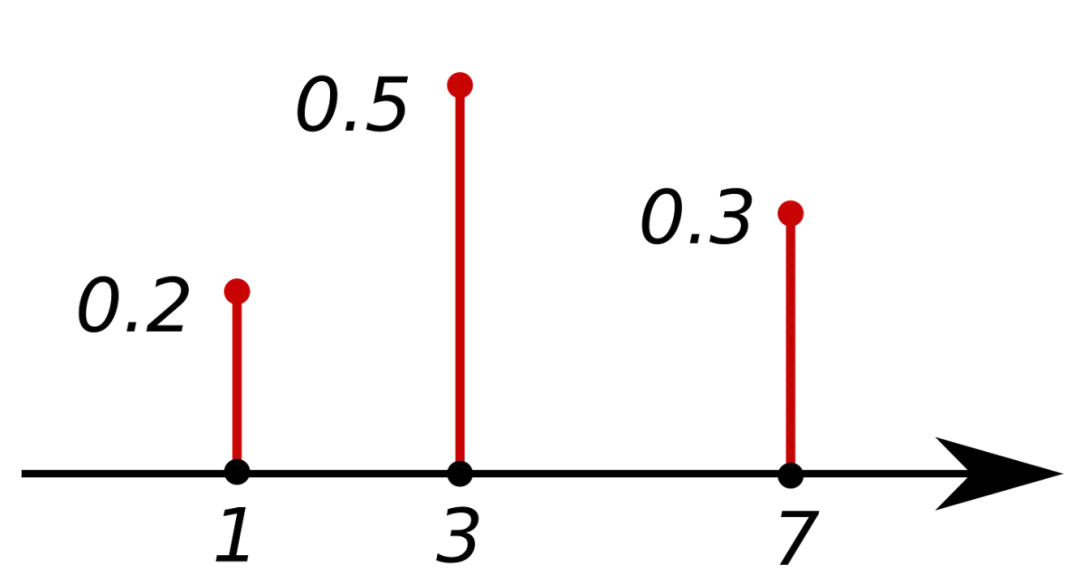
所以說，我們可以用表格和函數表示離散概率分布。我們也可以用圖形表示投擲骰子這個例子：

離散概率分布示例：伯努利分布

有些概率分布出現得非常頻繁，人們對它們進行了全面的研究，并命名了這些概率分布。伯努利分布（Bernoulli distribution）就是一個例子。它是描述有兩種可能結果的過程的概率分布，比如拋硬幣。

伯努利分布的概率質量函數為：

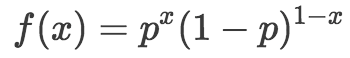
這里，x表示結果，值為1或0. 所以我們可以說正面 = 1，反面 = 0. p是表示結果為1的概率的參數。所以在扔均勻硬幣問題中，扔出正面或反面的概率是0.5，因此我們令p = 0.5.

我們經常想要明確標出概率質量函數中包含的參數，所以伯努利分布的概率質量函數可以表示為：

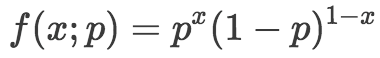
注意，這里我們使用分號隔開輸入變量和參數。

概率密度函數：連續概率分布

有時我們關心具有連續結果的隨機變量的概率。例如，從某個族群中隨機抽取的成人的身高，出租車司機等待下一個乘客的時間。在這些例子中，用連續概率分布描述隨機變量更合適。

當我們使用概率函數描述連續概率分布時，我們稱其為概率密度函數（probability density function），通常縮寫為pdf.

概率密度函數的概念比概率質量函數要稍微復雜一點，不過別擔心，我們能夠理解。我覺得先講一個連續概率分布的例子，再討論連續概率分布的性質，比較容易理解。

連續概率分布示例：正態分布

正態分布大概是所有概率和統計學問題中最常見的分布了。它如此常見的原因之一是中央極限定理。本文不會深入介紹這個定理，不過你可以參考Carson Forter寫的博客文章The Only Theorem Data Scientists Need To Know，其中解釋了這個定理是什么，還有它和正態分布的關系。

正態分布的概率密度函數定義為：

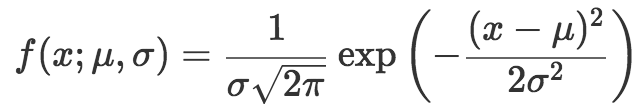
其中，參數（分號后的符號）μ表示均值（分布的中心點），σ表示標準差（分布的散布程度）。

如果我們將均值設為零（μ=0），標準差設為1（σ=1），那么我們將得到如下圖所示的分布：

正態分布是一個無限支持的連續單元概率分布。無限支持意味著我們可以為負無窮大到正無窮大之前的所有結果計算概率密度函數值。在數學上，我們有時稱其支持整條實直線（vhole real line）

連續概率分布性質

首先需要注意的是縱軸從0開始向上延伸。這是概率密度函數需要遵守的規則。概率密度函數的任何輸出值大于等于零，或者說，輸出非負：

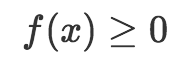
然而，和概率質量函數不同，概率密度函數的輸出不是概率值。這是一個極為重要的差別。

要從概率密度函數求得概率，我們需要找到曲線下的面積。例如，假設我們的樣本分布均值 = 3，標準差 = 1，我們在下圖中畫出結果位于0到1之間的概率：

數學上表達為：

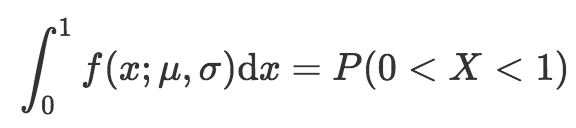
上式的意思是，概率密度函數0到1之間的積分（等式左邊）等于隨機變量的結果位于0到1之間的概率（等式右邊）。

原諒我沒有明確地介紹積分是什么，積分是如何工作的（我在本系列的邊緣化一文中簡短地介紹了積分的概念，但沒有涉及如何計算積分）。如果你不了解積分，那么目前而言你需要知道的是積分是一種求曲線下面積的方法，在這里給我們提供結果的概率。也許我需要撰寫一個簡短的系列，初步介紹微積分。

現在我們看到了概率密度函數的另一個性質。也就是兩個結果之間的概率，是概率密度函數在這兩點間的積分（等價于求出概率密度函數在兩點之間的曲線下的面積）。數學上，這可以表示為：

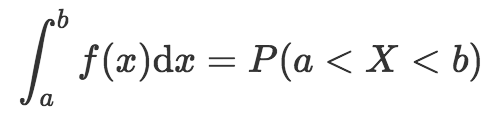
別忘了我們仍然需要遵循概率分布的規則，也就是所有可能結果之和等于1. 如果我們將范圍設定為“負無窮大”到“正無窮大”，那么就可以覆蓋所有可能的情形。因此，對概率密度函數而言：

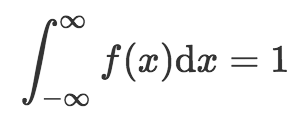
也就是說，負無窮大到正無窮大之間的曲線下面積等于1.

連續概率分布重要的一個性質（可能看起來很怪異）是隨機變量取得特定結果的概率為0. 例如，如果我們嘗試求解結果等于數字2的概率，我們將得到：

這個概念可能看起來很詭異，但如果你理解微積分，就比較容易理解這點。本文不會介紹微積分。相反，我想從中總結出一點，我們只討論兩個值之間的概率，或者討論出現大于或小于特定值的結果的概率。我們不討論結果等于特定值的概率。

眼尖的讀者可能注意到我用了“小于號（<）”和“大于號（>）”，而不是“大于等于號（≤）”和“小于等于號（≥）”。就連續概率分布而言，這實際上并沒有關系，兩者是一樣的。

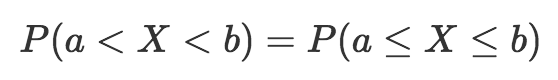
所以隨機變量取a和b之間的值的概率等于取a和b之間（含）的概率。

參數重要性

我們之前提到，參數可以改變函數的輸出值，在概率分布上也是一樣。

上圖是兩個正態分布的概率密度函數的圖像。藍色分布的參數值為μ=0、σ=1，而紅色分布的參數值為μ=2、σ=0.5.

很明顯，使用錯誤的參數值會得到離你的期望相差很遠的結果。

總結

哇！這篇文章比我預想的要長很多。讓我們總結一下要點：

概率分布是結果及相應概率的列表。

我們可以用表格羅列小分布的結果和概率，但大分布用函數概括更方便。

離散概率分布的表示函數稱為概率質量函數。

連續概率分布的表示函數稱為概率密度函數。

表示概率分布的函數同樣遵循概率法則。

概率質量函數的輸出是概率，概率密度函數曲線下面積表示概率。

概率函數的參數在定義隨機變量結果概率上起關鍵作用。

我原本打算在這篇文章中介紹多元分布的，但是因為本文已經很長了，所以會在之后的文章中介紹。

現在你已經初步理解了什么是概率分布，請閱讀Sean Owen的Common Probability Distributions: The Data Scientist’s Crib Sheet。如果想要了解更多概率分布，可以查看維基百科上的列表（相當長的一個列表）。

一如既往地感謝閱讀本文。我希望這篇文章幫助你學到了一點東西。歡迎留言評論和提問。