【導(dǎo)讀】線性代數(shù)是一種連續(xù)的、非離散的數(shù)學(xué)形式，許多計(jì)算機(jī)科學(xué)家對此缺乏應(yīng)用經(jīng)驗(yàn)，掌握線性代數(shù)對理解深度學(xué)習(xí)算法至關(guān)重要。今天AI科技大本營就為大家整理了學(xué)習(xí)過程中需要必備的線性代數(shù)知識(shí)，并附上代碼實(shí)現(xiàn)，幫助大家加深理解。

為什么數(shù)學(xué)是必要的？

線性代數(shù)、概率論和微積分都是機(jī)器學(xué)習(xí)的“語言”。學(xué)習(xí)這些科目將有助于深入了解底層的算法機(jī)制和開發(fā)新的算法。從較低的層級來看，深度學(xué)習(xí)背后的一切都是以數(shù)學(xué)為基礎(chǔ)的。因此，理解基礎(chǔ)的線性代數(shù)對于探索深度學(xué)習(xí)和上手與深度學(xué)習(xí)相關(guān)的編程來說是必要的。

深度學(xué)習(xí)中的核心數(shù)據(jù)結(jié)構(gòu)由標(biāo)量、向量、矩陣和張量組成。從編程的角度來說，我們只需運(yùn)用這些知識(shí)就能解決所有基本的線性代數(shù)問題。

參考閱讀：

https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.1-Scalars-Vectors-Matrices-and-Tensors/

標(biāo)量

標(biāo)量僅用于表達(dá)值的大小，也是零階張量的一個(gè)例子。符號 x ∈ ? 表示標(biāo)量 x 屬于實(shí)數(shù)值數(shù)組“ ? ”。

在深度學(xué)習(xí)中我們比較關(guān)注以下幾個(gè)數(shù)集，?、?和?。? 表示正整數(shù)集（1,2,3，...）。 ? 表示整數(shù)集，它包含了正值、負(fù)值和零值。 ? 表示可以由兩個(gè)整數(shù)所構(gòu)成的分?jǐn)?shù)進(jìn)行表達(dá)的有理數(shù)數(shù)集。

Python 中內(nèi)置了少數(shù)幾種標(biāo)量類型，如 int，float，complex，bytes，Unicode。而在 Python 庫 NumPy中，有 24 種新的基本數(shù)據(jù)類型來描述不同類型的標(biāo)量。

參考閱讀：

https://docs.scipy.org/doc/numpy-1.14.0/reference/arrays.scalars.html

如何在Python中定義和運(yùn)算標(biāo)量？

以下代碼片段解釋了基礎(chǔ)的標(biāo)量（Scalars）運(yùn)算。

參考閱讀：

https://gist.github.com/vihar/fbd3406bd9ba2402465fb1c8f3d8b3a6#file-scalars-py

返回如下：

以下代碼片段用于檢驗(yàn)所給的變量類型是否為標(biāo)量。

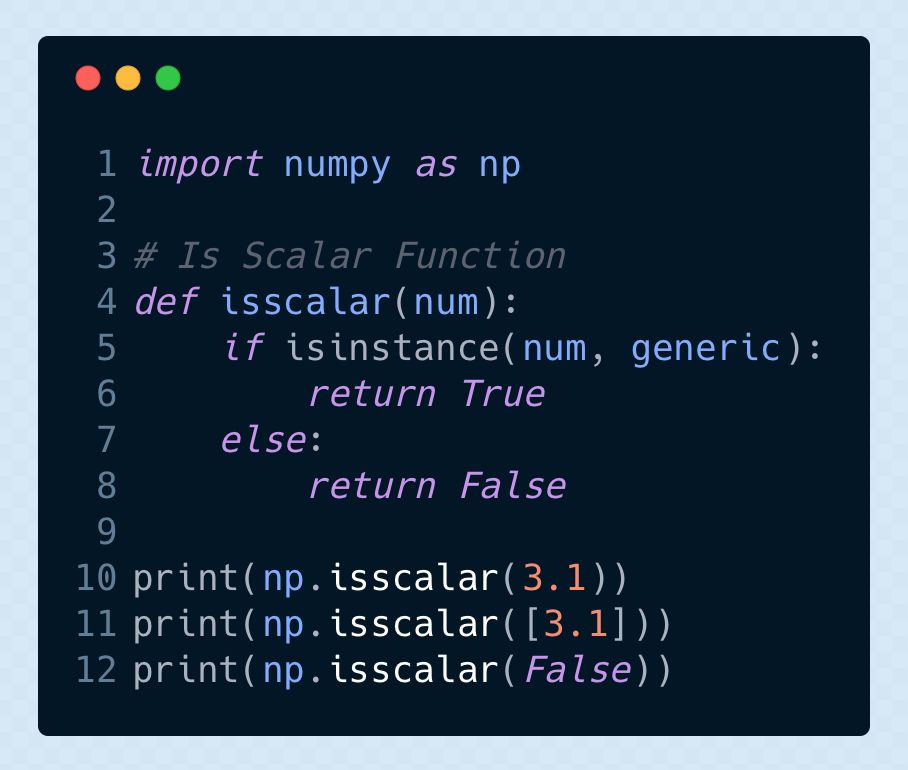
參考閱讀：

https://gist.github.com/vihar/b9ef648d47c1cb3db977f13fd3071dc6#file-is_scalar-py

返回如下：

向量

向量是由多個(gè)單個(gè)數(shù)字組成的有序數(shù)組，也是一階張量的一個(gè)例子。向量是向量空間中的片段。向量空間則可以被認(rèn)為是在特定長度（或維度）中所有可能存在的向量集合。我們通常說的現(xiàn)實(shí)世界中的三維空間，在數(shù)學(xué)里可以用向量空間表達(dá)為 ? ^ 3。

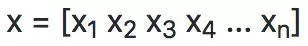
為了清晰明確地標(biāo)示向量中的必要成分，向量中的第 i 個(gè)標(biāo)量元素被記做 x[i] 。

在深度學(xué)習(xí)中，向量通常表示特征向量，它的原始成分則表示特定特征的相關(guān)程度。這些元素可以包括如二維圖像中一組像素的強(qiáng)度的相關(guān)重要性，或是金融工具的橫截面的歷史價(jià)格值。

如何在 Python 中定義和運(yùn)算向量？

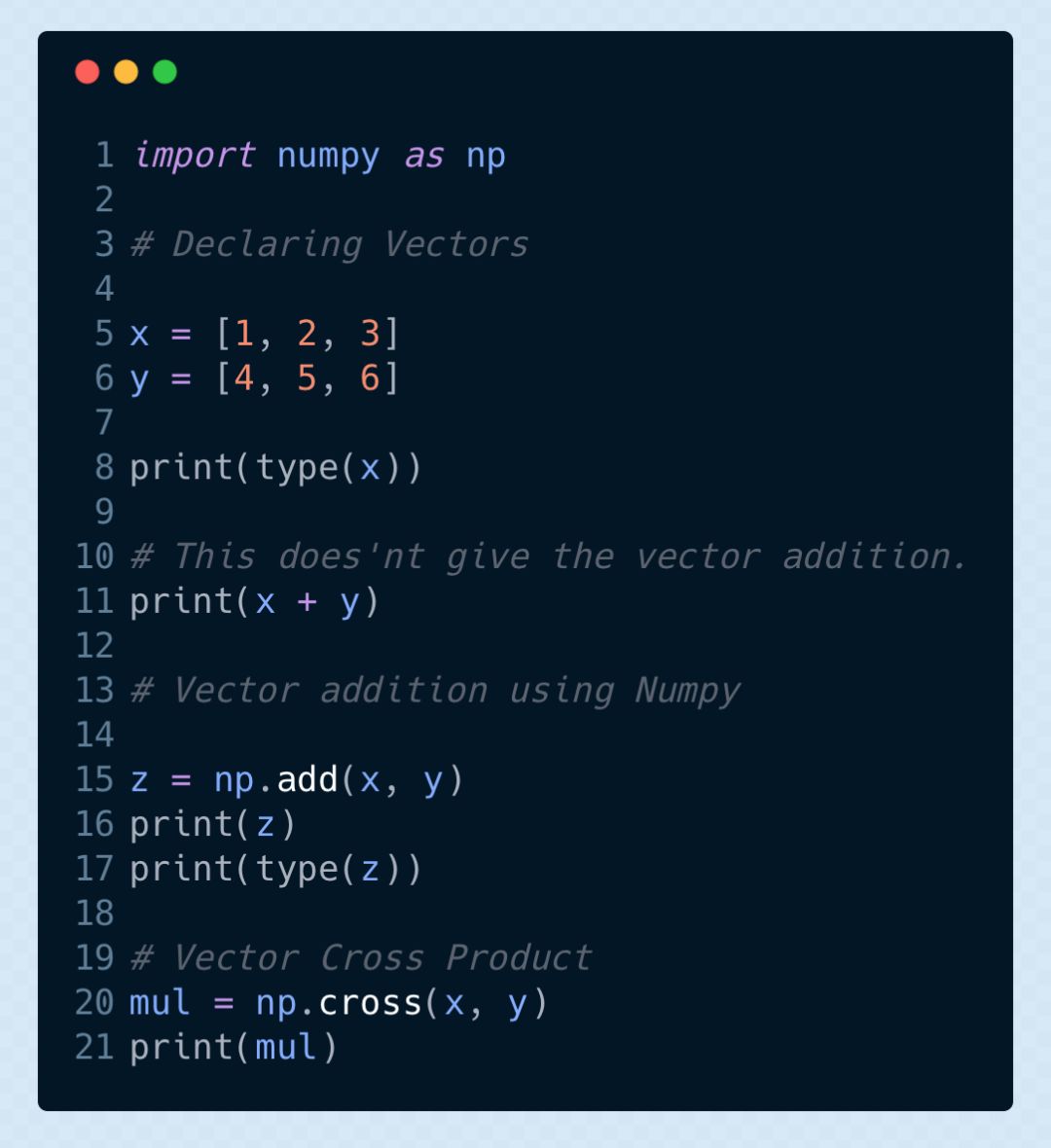
參考閱讀：

https://gist.github.com/vihar/7ede36aa2f5ba5e7f70960225a2d351e#file-vectors-py

返回如下：

矩陣

矩陣是由數(shù)字構(gòu)成的矩形陣列，是二階張量的一個(gè)例子。若 m 和 n 為正整數(shù)（ m，n ∈ N ），則 m × n的矩陣中包含 m * n 個(gè)元素，由m 行和 n 列構(gòu)成。

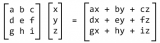
完整的 m × n 矩陣可寫做：

我們通常會(huì)將上面的矩陣縮寫為以下的表達(dá)式：

在 Python 里，我們會(huì)使用 numpy 庫來幫助我們創(chuàng)建 n 維的數(shù)組，這基本上可以被認(rèn)作為矩陣。我們將列表傳入名為 matrix 方法來定義一個(gè)矩陣。

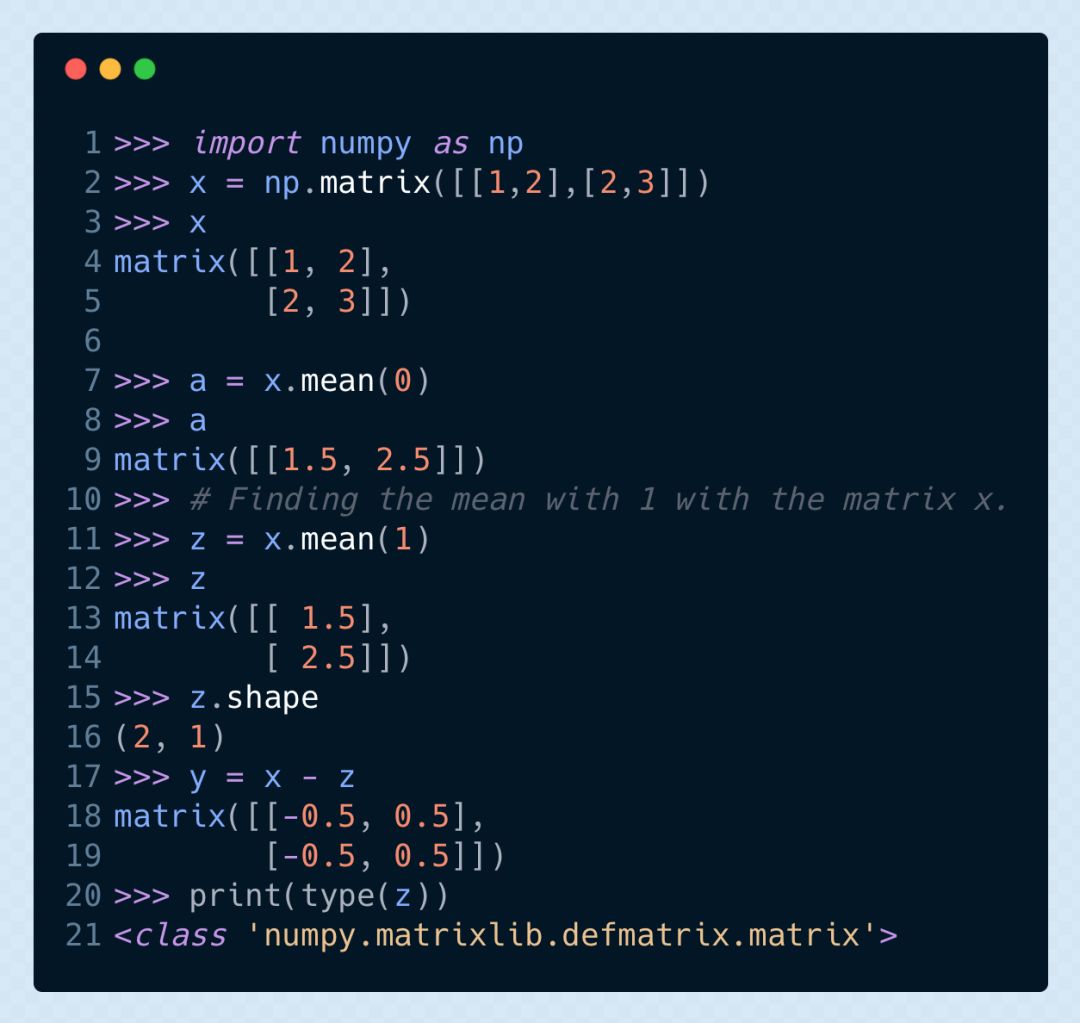
如何在 Python 中定義和運(yùn)算矩陣？

▌矩陣加法

矩陣可以與標(biāo)量、向量或其他的矩陣進(jìn)行相加。每一種加法都有一個(gè)精確的定義。這些技巧在機(jī)習(xí)和深度學(xué)習(xí)有著非常廣泛而頻繁的使用，所以它們值得你去熟悉。

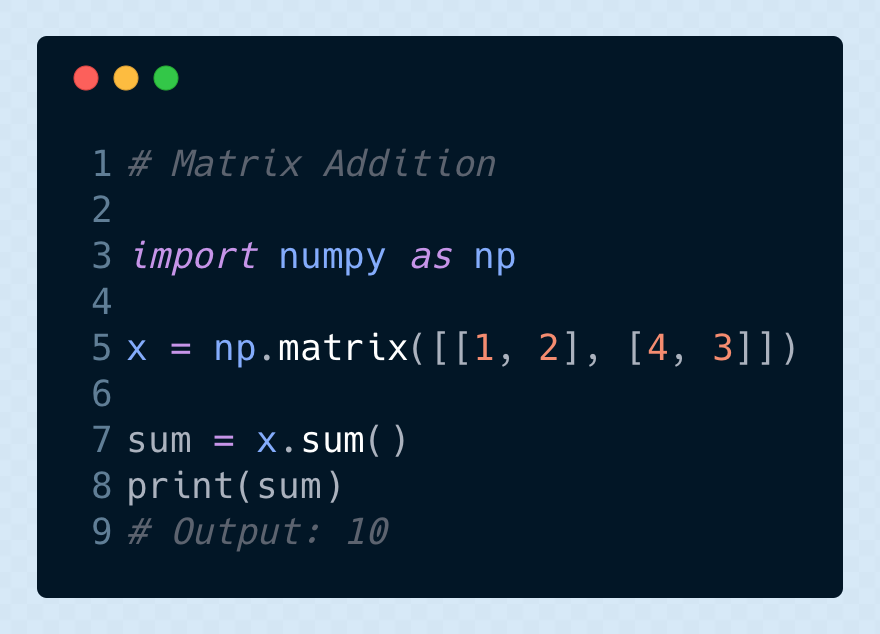
參考閱讀：

https://gist.github.com/vihar/1bdc39d126b4772f5a8e9d0b5185625f#file-matrix_addition-py

▌矩陣與矩陣的加法

C = A + B（ A 和 B 的形狀應(yīng)當(dāng)一致）

方法 shape 能夠返回矩陣的形狀，方法 add 會(huì)將傳入的兩個(gè)作為參數(shù)的矩陣相加，并返回相加的總和。若兩個(gè)作為參數(shù)的矩陣的形狀不一致，該方法則會(huì)提示存在“不能相加”的錯(cuò)誤。

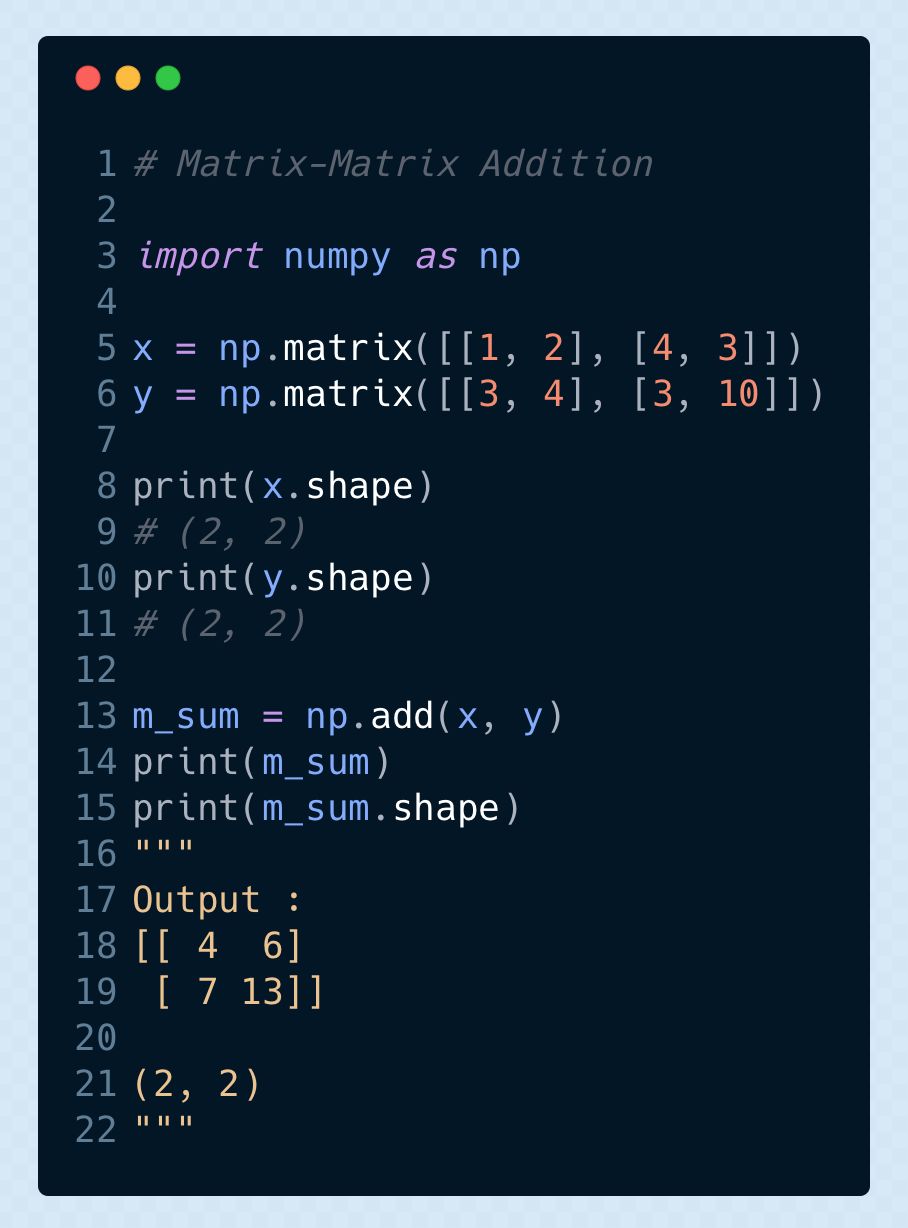
參考閱讀：

https://gist.github.com/vihar/b25716665d72d5e6b50c9149718df076#file-m_m_addition-py

▌矩陣與標(biāo)量的加法

將給定矩陣中的各個(gè)元素都與給定的標(biāo)量進(jìn)行相加

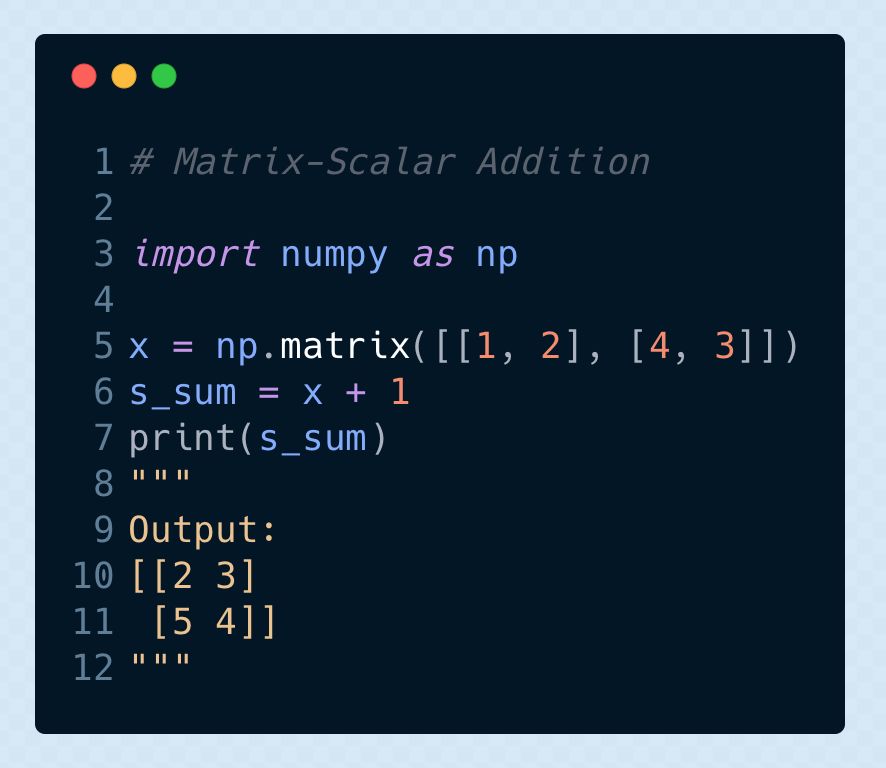
參考閱讀：

https://gist.github.com/vihar/ba689ec9a07b1c50f69269454373359a#file-matrix_s_addition-py

▌矩陣與標(biāo)量的乘法

將給定矩陣中的各個(gè)元素都與給定的標(biāo)量進(jìn)行相乘

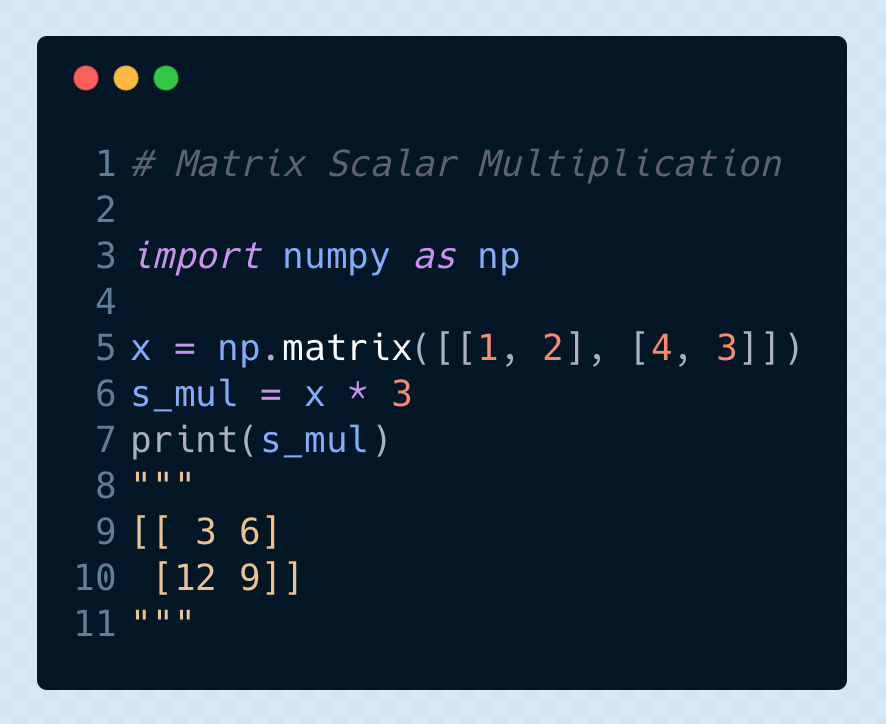
參考閱讀：

https://gist.github.com/vihar/5dcc0beeb7e48f0f271a75108401d34c#file-m_s_multiplication-py

▌矩陣之間的乘法

形狀為 m x n 的矩陣 A 與形狀為 n x p 的矩陣 B 相乘則會(huì)得到 形狀為 m x p 的矩陣 C

參考閱讀：

https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.2-Multiplying-Matrices-and-Vectors/

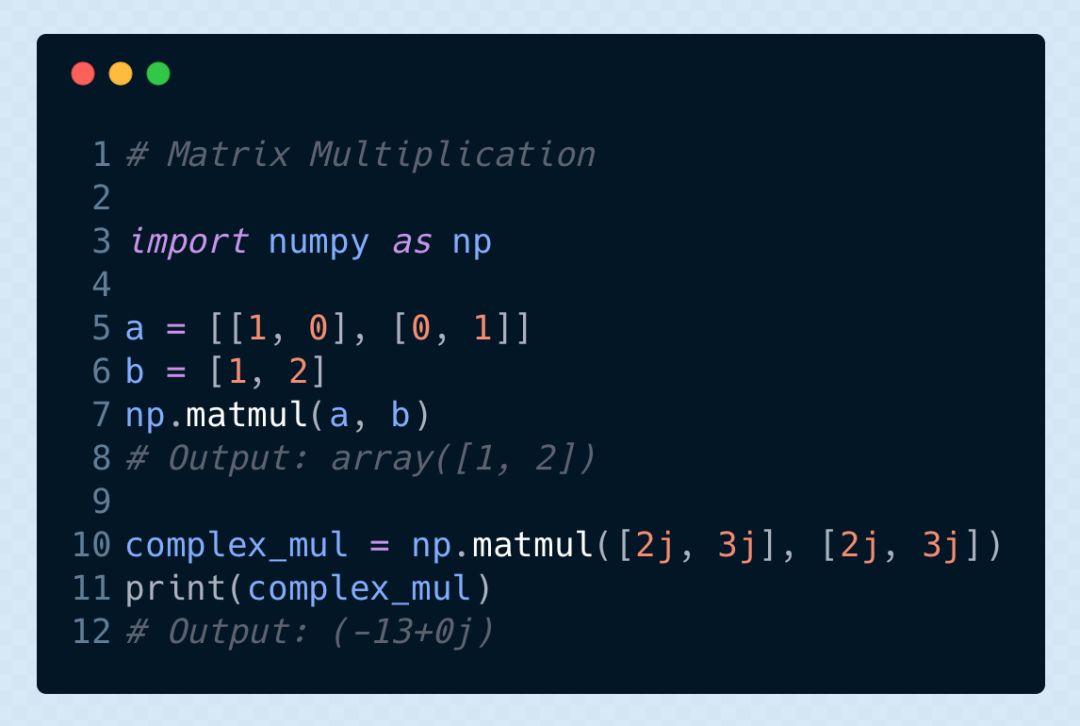
參考閱讀：

https://gist.github.com/vihar/1510e248a117f0af6a3843a4307de7b2#file-matrix_mul-py

▌矩陣的轉(zhuǎn)置

矩陣的轉(zhuǎn)置可以使一個(gè)行向量變成一個(gè)列向量，或反方向操作亦成立作亦成立：

A = [aij]m x n

AT = [aji]n × m

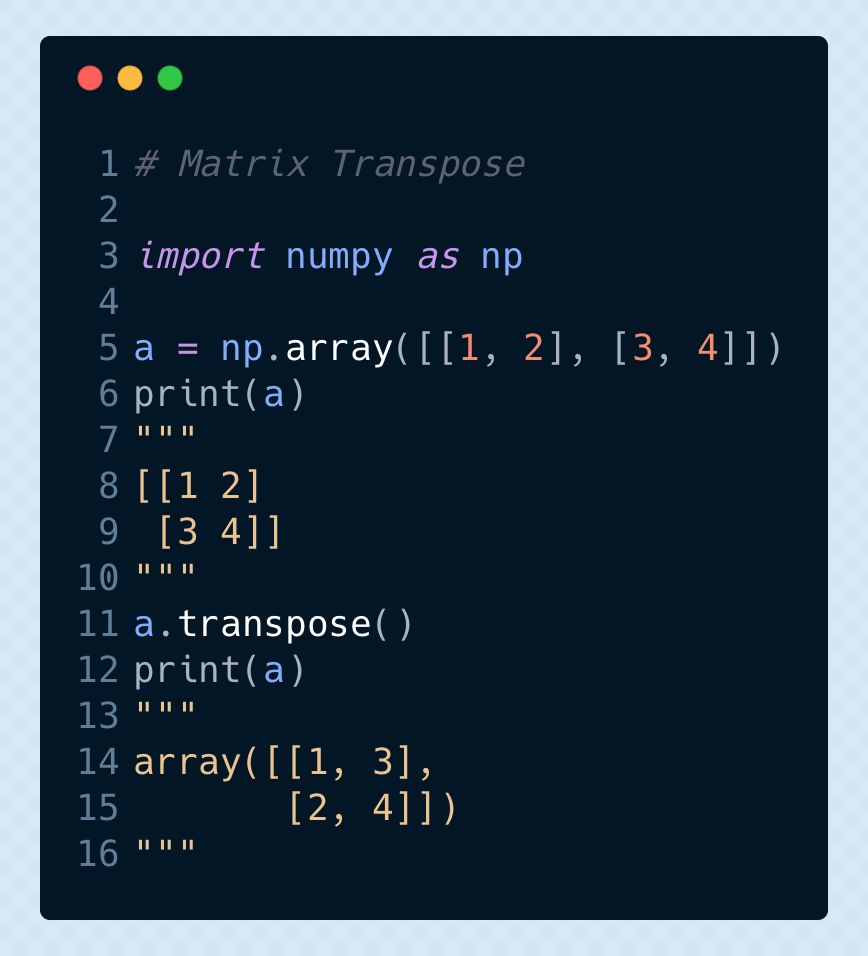
參考閱讀：

https://gist.github.com/vihar/3f2091377b3a1f36c402a203f25ffe33#file-martix_transpose-py

張量

籠統(tǒng)的來講，張量包含了標(biāo)量，向量，矩陣。有些時(shí)候，例如在物理及機(jī)器學(xué)習(xí)中，使用超過二階的張量是非常必要的。

參考閱讀：

https://refactored.ai/track/python-for-machine-learning/courses/linear-algebra.ipynb

我們通常不會(huì)將矩陣進(jìn)行嵌套來表示張量，而是會(huì)使用像 tensoTflow 或者 PyTorch 這樣的 Python 庫來對張量進(jìn)行表示張量 PyTorche 中定義一個(gè)簡單的張量

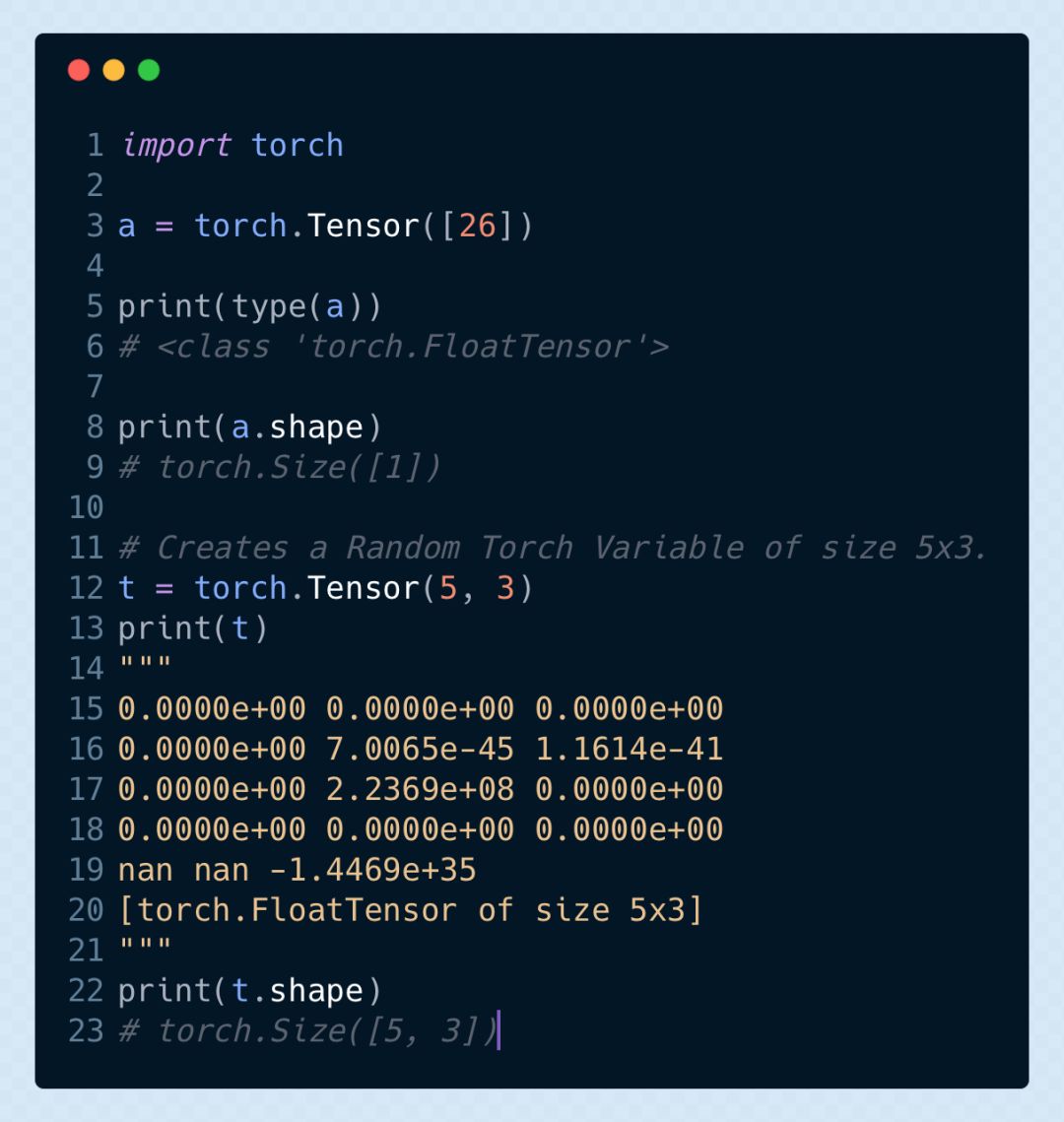
參考閱讀：

https://gist.github.com/vihar/eb78a6171de9740b128cbff21fc0b6ea#file-tensors-py

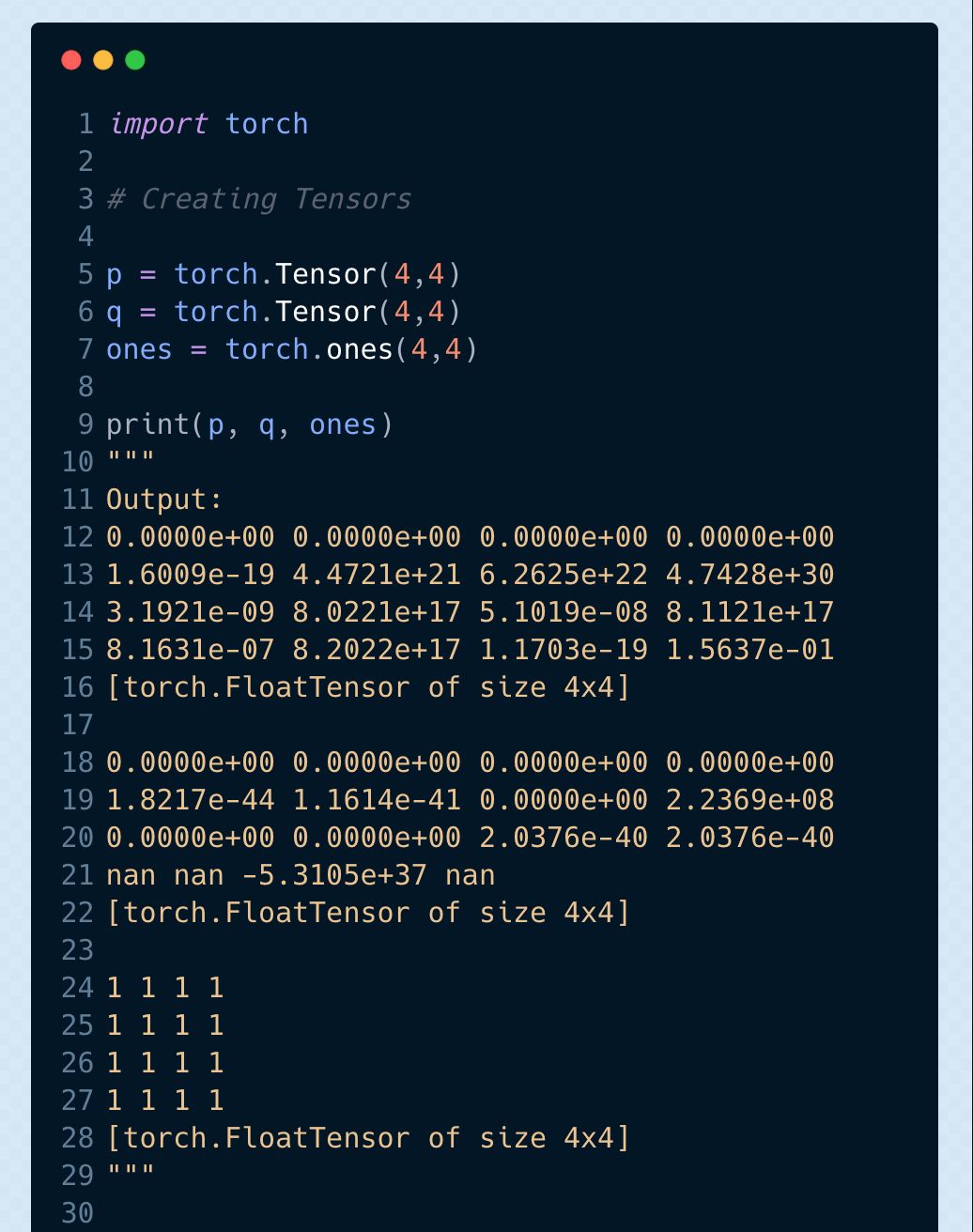
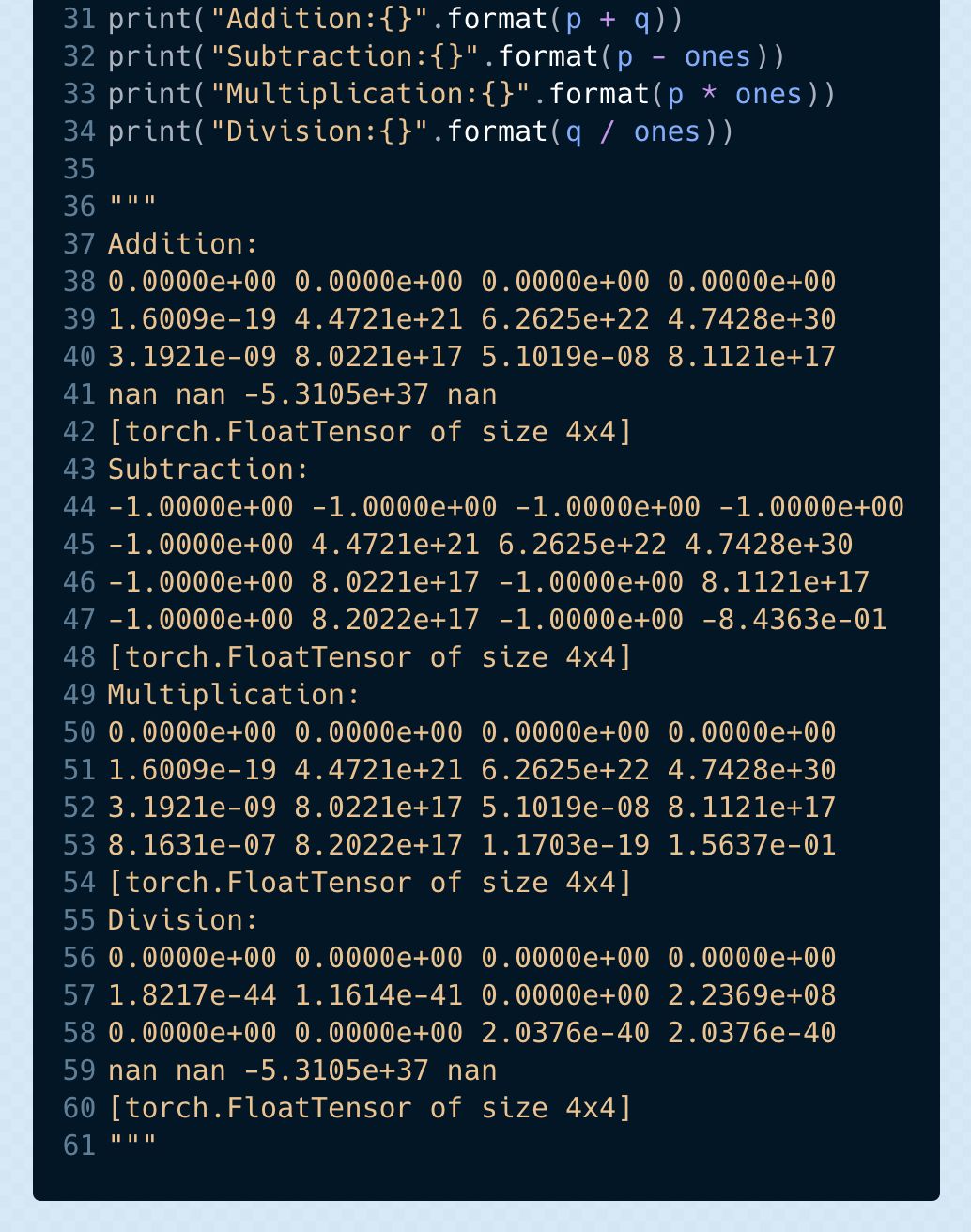
一些在 Python 中其他的張量的運(yùn)算操作

src：

https://gist.github.com/vihar/7b03ca54e4fe811e1053e09bdc1278b5#file-tensor_operations-py