1、引言

中高壓大容量電機的變頻調速改造是國家節能減排工作的重點。中高壓變頻器的主功率電路普遍采用多電平逆變器拓撲，以達到降低功率器件的耐壓等級、減小dv/dt、改善諧波等效果［1］。其中，H橋級聯型結構的多電平逆變器在中高壓電機的變頻調速領域技術最為成熟，應用最為廣泛。

目前，中高壓變頻器的產品中，電機調速控制策略多采用V/F控制或矢量控制（又稱磁場定向控制），而直接轉矩控制（Direct Torque Control，簡稱DTC）方面的研究與應用較少，實現難度較大。主要原因之一在于多電平拓撲的開關管數目眾多，造成傳統DTC所需要的開關向量表非常復雜。另外，傳統DTC采用滯環比較器，逆變器開關頻率不固定，難以數字實現，生成多電平波形較為困難，電流、轉矩脈動較大。

實現DTC等高性能調速策略需要檢測電機的轉速，但速度傳感器的安裝增加了系統的復雜性、成本和維護要求，降低了可靠性和魯棒性。

本文針對級聯多電平的特點，將錯時采樣空間矢量調制法和無速度傳感器技術引入到級聯多電平直接轉矩控制中，解決了傳統DTC應用在多電平領域所存在的開關向量表復雜、波形質量不好、轉矩脈動大等問題，具有直流電壓利用率高、功率單元使用均衡、諧波含量好、方法簡單、易于數字實現等優點。利用Matlab/Simulink對這一方法進行了仿真驗證。

2 、多電平直接轉矩控制的難點

傳統的直接轉矩控制采用磁鏈與轉矩的砰—砰控制，根據它們的變化與定子磁鏈所在的空間位置直接選擇電壓空間矢量的開關狀態，獲得快速的轉矩響應。但是其實際轉矩在滯環比較器的上下限內脈動，開關頻率也不固定。一種改進方案是將空間矢量調制（SVM）方法與DTC相組合，對轉矩進行閉環PI調節，以電壓空間矢量調制模塊取代開關向量表，產生PWM波控制逆變器的開關狀態，可使開關頻率恒定，轉矩脈動也大幅減小。

然而，在多電平領域，逆變器的基本空間矢量數目眾多，對于每相n個H橋級聯單元即 級級聯的多電平逆變器，其基本空間矢量數目為（2n+1） 3個。每相3單元的高壓變頻器基本空間矢量多達343個，而對于每相6單元的高壓變頻器，這個數目達到了2197個。如此繁多的基本空間矢量使空間矢量選擇算法變得非常復雜。另外，空間矢量的選擇要考慮功率單元的開關負荷均衡，這就對算法提出了更高的要求。因此，在電平數較多的情況下，空間矢量算法實現困難，也難以滿足實時控制的要求。

為克服上述問題，在級聯多電平中采用錯時采樣空間矢量調制（Sampe-Time-Staggered Space Vector Modulation，簡稱STS-SVM）策略，能大大降低空間矢量選擇的復雜度，并且能夠實現開關負荷的自動均衡，執行效率高，易于實現無速度傳感器DTC等高性能實時控制。

3 、錯時采樣SVM策略

錯時采樣空間矢量法最早是應用在如圖1所示的組合變流器結構，此變流器由N個3相6開關管的逆變器單元組成，輸出通過變壓器耦合。STS-SVM的基本思想是在每個變流器單元中按照傳統兩電平空間矢量的方法進行參考電壓的采樣，采樣周期為Ts，將相鄰單元的采樣時刻錯開Ts/N。這樣，系統等效的基本空間矢量數目大大增加，得到的輸出電壓具有多電平的形式，相電壓電平數為2N+1。

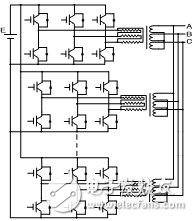
圖1 組合變流器拓撲

組合變流器與3相H橋級聯型多電平逆變器在拓撲上具有轉換等效關系。將圖2（a）中的兩級多電平變流器經變換后可等效為圖2（b）中的一級3相H橋結構，等效的開關管在兩幅圖中以相同的編號表示，即一級H橋中左橋臂的開關管和右橋臂的開關管可分別等效為多電平變流器的兩個3相6橋臂單元。這樣就可將STS-SVM調制法用于一級3相H橋。具體方法是用STS-SVM方法得出圖2（a）中的開關管的驅動信號，去驅動圖2（b）中相同編號的開關管。由于兩級變流器中N=2，因此兩個單元的采樣時刻錯開Ts/2。轉化到圖2（b）中，相當于對一級3相H橋逆變器左橋臂的6個開關管和右橋臂的6個開關管分別進行相同的幅度和頻率調制比下的兩電平空間矢量調制，并且要使兩者參考電壓的采樣時刻錯開Ts/2。

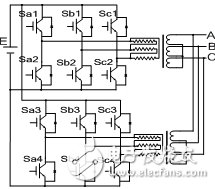
（a）兩級多電平變流器

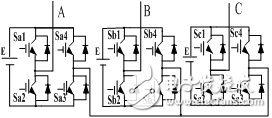
（b） 一級三相H橋逆變器

圖2 兩級組合變流器與一級三相H橋逆變器的等效關系

根據上述思想進行擴展，對于n級H橋級聯的逆變器，可以等價為2n個單元的組合變流器，相鄰的兩級H橋單元同一側橋臂的采樣時 刻應相互錯開Ts/2n。

由上述分析可以得到在n級H橋級聯型逆變器中應用錯時采樣調制策略的實現方法。只要根據傳統兩電平空間矢量算法得出某一級H橋中三個同側橋臂的驅動信號，系統中其它各開關管的驅動信號即可通過相應的延時得到。兩電平空間矢量算法在主控制器中進行，延時可通過在主控制器外增加硬件單元來實現。這樣就大大減輕了主控制器的負擔，能夠適應快速實時控制的要求。

STS-SVM中，系統總體輸出電壓矢量的安排是自動完成的，由兩電平空間矢量算法得出的各個橋臂觸發波形自身具有對稱性和均衡性，因此總體開關負荷也是均衡的。

4、 STS-SVM無速度傳感器DTC系統

相對于普通的多電平空間矢量算法，STS-SVM控制算法簡單，開關負荷均衡，使得主控制器實現復雜的無速度傳感器直接轉矩控制等算法成為可能。

圖3為基于STS-SVM的級聯多電平無速度傳感器DTC控制系統的總體結構。圖中速度調節器、轉矩調節器、磁鏈調節器均為比例積分調節，轉矩調節器需要在PI調節前采用限幅，以免過大的轉矩誤差造成過電流沖擊。系統總采用STS-SVM模塊產生PWM波控制逆變器的開關狀態，摒棄了復雜的開關矢量表。另外，由于未使用滯環比較，系統的采樣頻率是固定的，更易于數字實現。

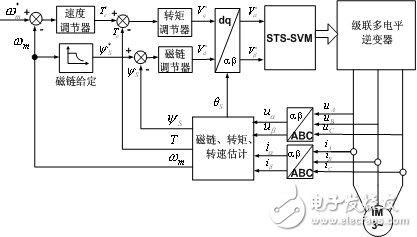
圖3 基于STS-SVM的無速度傳感器DTC系統結構

4.1 STS-SVM調制的多電平逆變器

此處，多電平逆變器為圖4（a）所示的三級H橋級聯型拓撲。STS-SVM模型中的驅動信號的產生通過兩電平空間矢量算法得出的調制波與各個開關管對應的三角波進行比較來獲得，如圖4（b）所示。各個三角載波存在一定的移相關系，這樣就等效地實現了采樣周期的相互錯開。

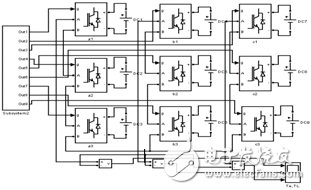
（a） 三級級聯多電平逆變器主電路

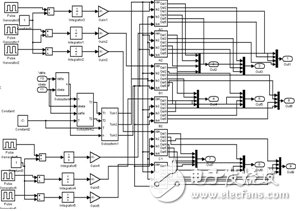
（b）STS-SVM驅動信號產生單元

圖4 級聯多電平主電路與PWM產生單元

4.2 磁鏈與轉矩觀測

定子磁鏈的估計大體上可以分為三種模型，即u-i模型，i-n模型，u-n模型。其中u-i模型中磁鏈表達式為

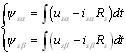（1）

其中，，us，is，Rs分別為定子磁鏈、電壓、電流值與定子電阻值，可見，u-i模型觀測定子磁鏈無需轉速信息，唯一所需了解的電動機參數是定子電阻Rs，因此十分適合在此處應用。

直接轉矩控制需要實測電磁轉矩Te作為反饋量，一般采用計算法。電磁轉矩具有多種不同的表達式，可以采用定子電流、轉子電流、定子磁鏈、轉子磁鏈中的任意2個參數來獲得電磁轉矩。在直接轉矩控制中，通常采用如下的公式計算Te：

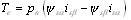（2）

其中，Pn為電機的極對數。

在Matlab/Simulink中建立磁鏈與轉矩觀測的模型，如圖5所示。

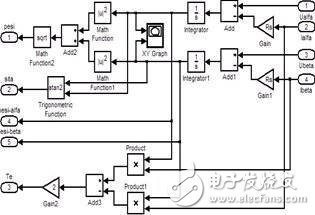
圖5 定子磁鏈與轉矩觀測模型

4.3 速度估計

基于模型參考自適應系統（Model Reference Adaptive System，MRAS）的轉速辨識實現較為方便，且具有對轉子電阻變化的完全不敏感性，電機參數變化對轉速估算的影響也較小。轉子磁鏈的電壓模型與電機轉速無關，而轉子磁鏈的電流模型與電機轉速有關，因此選擇轉子磁鏈的電壓模型作為參考模型，而選擇轉子磁鏈的電流模型作為可調模型。

由于在磁鏈觀測中已經估算出定子磁鏈，因此參考模型可以用定子磁鏈表示：

其中Tr=Lr/Rr為轉子時間常數，Rr為轉子電阻，為轉子角速度。

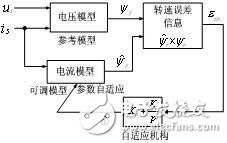
圖6 利用轉子磁鏈估計轉速的MRAS方案

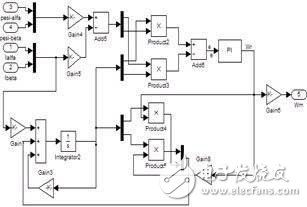
圖7 轉速估計模型

5 仿真結果及分析

在Matlab/Simulink中建立了整個系統的仿真模型。其中，電機模型采用軟件自帶的兩級三相異步感應電機模型，參數為：額定功率PN =3730W，額定線電壓UN =380V，額定頻率fN =50Hz，轉子電阻Rr=1.083Ω，定子電阻Rs=1.115Ω，定子、轉子電感Ls= Lr=0.2097H，定轉子互感Lm=0.2037H，轉動慣量J=0.02kgg㎡。逆變器每級直流電源電壓為104V，采樣周期Ts=952μs。

在0.3s處突加6Ngm的負載。各個變量的仿真波形如圖8所示。

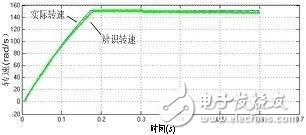
（a）辨識轉速與實際轉速

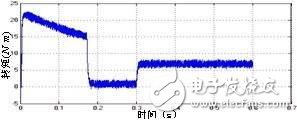
（b）轉矩動態相應

（c）定子磁鏈 （d）電流

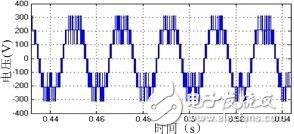
（e）相電壓

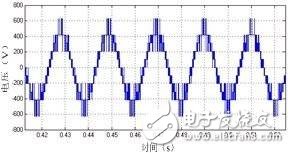
（f）線電壓

圖8 系統仿真波形

由仿真波形可以看出，電機啟動后0.2s，系統基本進入穩定狀態；辨識轉速能較好地估計與跟蹤實際轉速；相電壓輸出7電平；線電壓輸出13電平；電流波形良好；穩態時磁鏈與轉矩脈動都比較小；啟動過程中定子磁鏈能很快達到給定值，并保持圓形；啟動時轉矩迅速達到限幅值（23Ngm），之后逐漸回落到空載穩定值，加載時動態響應特性良好。

6 結論

本文將錯時采樣空間矢量調制方法、模型參考自適應方法與直接轉矩控制相結合，實現了級聯多電平變頻器的無速度傳感器直接轉矩控制，有實現簡單、可靠性高、轉矩脈動小等諸多優點，具有較好的實用價值。文中給出了各個部分的建模方法，通過仿真對這一方法進行了驗證。

責任編輯：gt