為了提高非圓車削中快速伺服刀架的跟蹤精度和抗干擾性,研制了一種自抗擾控制器。通過對執(zhí)行機構(gòu)建模分析,將模型中的非線性部分歸結(jié)為系統(tǒng)的內(nèi)擾,將加工過程中切削力干擾歸結(jié)為系統(tǒng)外擾,設(shè)計出相應(yīng)的擴張狀態(tài)觀測器,對系統(tǒng)內(nèi)、外擾的總和做出實時估計和補償。仿真實驗表明,自抗擾控制性能優(yōu)于傳統(tǒng)的PID控制。通過DSP(digital signal processor)編程,將自抗擾控制器應(yīng)用于非圓車削。切削加工試驗結(jié)果表明,自抗擾控制具有良好的控制品質(zhì),快速伺服刀架跟蹤精度控制在5μm以內(nèi)。
非圓數(shù)控車削是實現(xiàn)非圓截面零件高效、柔性、高精度加工的有效方法。非圓車削時,刀具在快速伺服刀架(fast tool servo,F(xiàn)TS)的驅(qū)動下,隨著主軸高速回轉(zhuǎn)沿工件徑向做快速往復(fù)運動。FTS的跟蹤精度是影響非圓截面零件輪廓精度的主要因素。FTS控制器設(shè)計面臨兩個技術(shù)難點:第一,如何提高FTS的伺服剛度,以減小變化的切削力對跟蹤精度的影響;第二,如何減小FTS執(zhí)行機構(gòu)的非線性和參數(shù)變化對跟蹤精度的影響。
目前,許多學(xué)者都對適于非圓車削的FTS控制器進(jìn)行了深入研究。文采用PID控制結(jié)合前饋補償?shù)姆绞剑O(shè)計出基于位置反饋和速度反饋的兩種干擾觀測器。文針對非圓車削中,跟蹤信號為有規(guī)律的周期信號這一特點,采用重復(fù)控制算法,并進(jìn)行了相應(yīng)的改進(jìn),增強了系統(tǒng)響應(yīng)的快速性。文采用模型參考自適應(yīng)控制,對FTS進(jìn)行控制,提高了系統(tǒng)的魯棒性和抗干擾能力。
自抗擾控制(active disturbance rejectioncontroller,ADRC)是一種基于誤差反饋的非線性控制方法,其原理簡單,可對系統(tǒng)的未建模動態(tài)和未知擾動做出很好的估計和補償,具有很強的適應(yīng)性和魯棒性。本文應(yīng)用自抗擾控制技術(shù),根據(jù)非圓車削對FTS控制器在跟蹤精度、響應(yīng)速度、抗擾動性等方面的要求,研制了自抗擾精密跟蹤運動控制器,并進(jìn)行仿真分析和切削試驗。
1 被控對象建模
非圓車削采用的FTS執(zhí)行機構(gòu)結(jié)構(gòu)見文,它采用音圈電機驅(qū)動原理,彈簧和滾動導(dǎo)軌復(fù)合支承,可近似為彈簧阻尼系統(tǒng),運動微分方程為
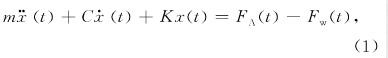
其中:m為運動部分質(zhì)量,K為執(zhí)行機構(gòu)內(nèi)彈簧的剛度系數(shù),C為阻尼因數(shù),F(xiàn)w為加工過程中的切削力,F(xiàn)A為電磁力。根據(jù)電磁力汁算公式,有FA(t)=nBLI(t),其中:n為線圈匝數(shù),B為磁通密度,L為有效線圈長度,I為電流強度。
對執(zhí)行機構(gòu)進(jìn)行控制時,輸入為電壓控制信號,通過功率放大器轉(zhuǎn)換為電流輸出,轉(zhuǎn)換的關(guān)系為I(t)=ku(t),運動方程可寫為如下形式:
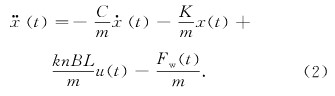
然而,執(zhí)行機構(gòu)在實際工作過程中,由于線圈磁通不均勻和磁阻推力,使得執(zhí)行機構(gòu)的推力與線圈電流并不呈線性關(guān)系,從而給控制帶來了較大的難度。同時,由于切削力在加工過程中是實時變化的,也對系統(tǒng)的穩(wěn)定性產(chǎn)生了很大的影響。
2 自抗擾精密跟蹤運動控制器的設(shè)計
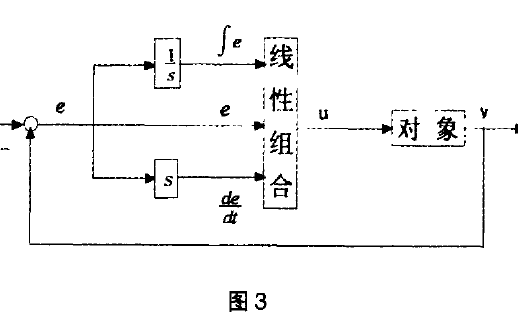
圖1給出了自抗擾控制器結(jié)構(gòu)。
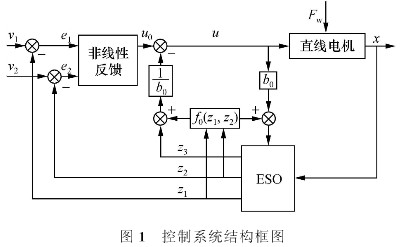
典型的自抗擾控制器包括跟蹤微分器(trackingdifferential,TD)、擴張狀態(tài)觀測器(extended stateobserveF,ESO)和非線性反饋控制器3部分。n階TD的作用是給出不可微輸入信號的跟蹤信號及其l至n-l階微分信號。TD產(chǎn)生的信號相對于輸入信號有少許滯后,此外,非圓零件截面形狀一般用可微函數(shù)表示,直接對該函數(shù)求導(dǎo)就可以獲得參考信號的微分值。因此,本控制器去掉了TD環(huán)節(jié)。。ESO可實時估測出被控對象的各階狀態(tài)變量和系統(tǒng)的總擾動中的未知部分(包括內(nèi)擾和外擾),并給予補償。非線性反饋控制器將TD的輸出信號與由ESO觀測到的相對應(yīng)的狀態(tài)變量作差后,經(jīng)過非線性組合,產(chǎn)生未包含擾動在內(nèi)的控制量,達(dá)到提高系統(tǒng)的快速性,減小超調(diào)量的目的。
設(shè)FTS執(zhí)行機構(gòu)在實際工作過程中,推力FA與輸入u之比為一未知函數(shù)b(t)。則執(zhí)行機構(gòu)的運動微分方程可寫為:


3 仿真分析
為了考察自抗擾控制器抵抗外界擾動和內(nèi)部參數(shù)變化的能力,利用Matlab編程,分別進(jìn)行了仿真分析。為了更直觀地說明問題,同時還對PID控制進(jìn)行了仿真。在仿真編程時,被控對象采用二階模型。由于實際被控對象中的未建模環(huán)節(jié),在比例系數(shù)過大時將造成系統(tǒng)不穩(wěn)定。為了盡量準(zhǔn)確地反映實際加工過程中切削力的影響,仿真過程中對兩種控制算法的比例系數(shù)根據(jù)實際情況進(jìn)行了限制。在此限制下,通過反復(fù)調(diào)節(jié),分別整定出使跟蹤誤差最小的控制參數(shù),并用這組參數(shù)進(jìn)行了下面的仿真實驗。
3.1 抵抗外界擾動的性能分析
非圓車削中FTS所受到的外界擾動主要是變化的切削力,故仿真分析時干擾信號采用加工過程中兩種典型的切削力信號。仿真采用的參考信號為非圓車削過程中刀具沿工件徑向理想的往復(fù)運動軌跡。以主軸轉(zhuǎn)速1 200 r/min,加工橢圓度為0.4 mm的活塞為例,刀具運動方程為y=100(cos(251.33t/s)-1)。
試驗1:從第0.05 s開始,加入幅值為50 N,頻率與刀具運動頻率相同的切削力信號Fw/N=50(1-cos(251.33t/s)),這相當(dāng)于由圓形截面車削形成非圓截面的工況。仿真結(jié)果如圖2所示,其中縱坐標(biāo)為跟蹤誤差e,橫坐標(biāo)為時間t。
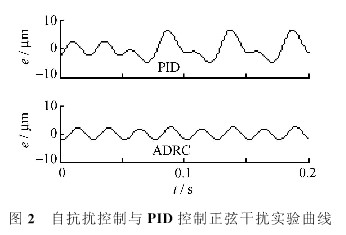
由圖2可以看出,PID控制在加入干擾信號后,誤差幅度明顯增大,誤差曲線規(guī)律也有明顯改變。而自抗擾控制在加入干擾信號后,所受到的影響基本被消除,誤差范圍與未加入干擾前相當(dāng),說明自抗擾控制有良好的抗干擾特性,對于因切深變化而產(chǎn)生的交變切削力,抑?jǐn)_能力要強于PID控制。
試驗2:從第0.05 s開始,加入幅值為50 N,頻率與刀具運動頻率相同的方波切削力信號,這相當(dāng)于加工帶有活塞削孔橢圓形截面的工況。兩種控制方法的跟蹤誤差仿真結(jié)果如圖3所示。
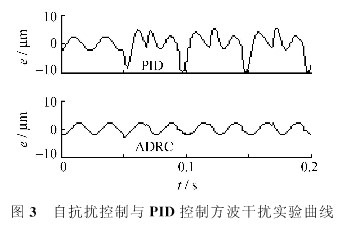
從圖3可見,方波切削力干擾信號由于具有力突變的性質(zhì),所以對控制系統(tǒng)的影響要大于正、余弦干擾信號。對于自抗擾控制,在切削力發(fā)生突變時,誤差僅發(fā)生小幅波動,對整體的誤差范圍沒有影響。但對于PID控制,這種干擾所帶來的誤差波動是相當(dāng)劇烈的。因此,對于因凹槽等原因而產(chǎn)生的方波規(guī)律變化的切削力,自抗擾控制的抑?jǐn)_能力也強于PID控制。
3.2 抵抗內(nèi)部參數(shù)變化的性能分析
為了檢驗控制算法抵抗內(nèi)部參數(shù)變化的能力,在上述參考信號的基礎(chǔ)上,從O.05 s開始,將FTS執(zhí)行機構(gòu)的輸出增益減小50%,試驗結(jié)果如圖4所示。
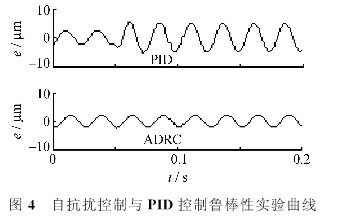
從圖4可見,增益減小50%后,PID控制的誤差范圍有了較為明顯的變化,而自抗擾控制的跟蹤效果幾乎沒有受到任何影響。這個試驗充分反映了自抗擾控制對被控對象模型不依賴的特性,其魯棒性強于PID控制。
4 切削試驗研究
4.1 試驗系統(tǒng)
切削試驗是在G-CNCP200型中凸變橢圓活塞數(shù)控機床上進(jìn)行的。該機床橫向和縱向運動為開環(huán)控制,交流伺服驅(qū)動。FTS機械結(jié)構(gòu)部分安裝在機床的橫向刀架上,驅(qū)動刀具實現(xiàn)精密往復(fù)運動。主軸采用變頻控制,可實現(xiàn)無級調(diào)速。FTS硬件包括DSP(digital signal processor)控制板,D/A轉(zhuǎn)換器,功率放大器和線性執(zhí)行機構(gòu)和線性光柵5部分。DSP控制器經(jīng)過算法運算后,通過數(shù)摸轉(zhuǎn)換器將模擬控制信號發(fā)送給功率放大器,經(jīng)放大后直接驅(qū)動機構(gòu)往復(fù)運動,其位置值通過尾部的光柵反饋回DSP控制板,形成一個閉環(huán)控制系統(tǒng)。
DSP控制板采用TMS320LS2407型DSP芯片。這種芯片主頻為30 MHz,支持32位加法及1616位乘法運算,并同時支持匯編語言和C語言編程。由于加工過程中采樣周期僅幾十微秒,為了盡量縮短控制周期,同時方便優(yōu)化程序代碼,本文采用匯編語言編程。由于該DSP控制板為定點DSF,所以在進(jìn)行浮點運算時,需要事先進(jìn)行定標(biāo)處理。同時,由于定點DSP在執(zhí)行開方等指數(shù)運算時,執(zhí)行效率較低,所以在編寫程序時,考慮將算法中的非線性函數(shù)做線性處理,以簡化程序,縮短控制周期。通過仿真實驗,簡化處理后,控制周期可縮短50%以上,而快速性略有下降,但對抗干擾性和魯棒性影響甚微,所以采用線性處理是必要且可行的。
4.2 切削試驗
切削試驗所用活塞試件材料為硬鋁(2A80),橢圓度分別為0.2、0.4、0.6、0.8mm,刀具材料為硬質(zhì)合金(YT3)。分別在主軸轉(zhuǎn)速800、l 000、1 200、1 400 r/min,切削深度0.05、0.1、0.2、0.3mm,進(jìn)給量0.05、0.1 mm/r條件下,進(jìn)行了多次正交切削試驗。
上述各種切削試驗中刀具跟蹤運動誤差控制在5μm以內(nèi)。圖5給出了主軸轉(zhuǎn)速1 200 r/min,進(jìn)給量0.05 mm/r,切深分別為0.05、0.1和0.2mm時刀具跟蹤運動誤差。在實驗過程中發(fā)現(xiàn),跟蹤誤差隨切削深度的增加而略有增加,但所加工活塞的橢圓度對誤差范圍的影響很小,因此,在加工大橢圓度活塞時將獲得很好的相對誤差值。
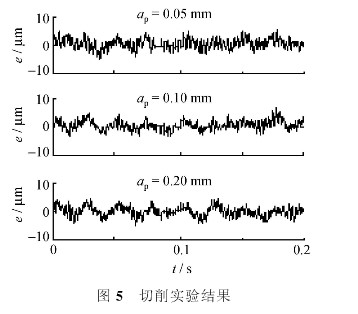
切削試驗結(jié)果表明,所設(shè)計的自抗擾精密跟蹤控制器能抵抗非線性變化的切削力的影響,跟蹤精度能滿足加工要求。但是,與仿真分析結(jié)果不同,切削時刀具跟蹤運動的誤差曲線包含許多毛刺,這是由于光柵反饋分辨率為0.5/μm,從而造成誤差曲線跳變,同時也影響了跟蹤精度;此外,DSP的定點運算功能限制了參數(shù)的取值和運算精度,從而也降低了跟蹤控制精度。
5 結(jié) 論
本文將自抗擾控制技術(shù)應(yīng)用于非圓數(shù)控車削中的快速伺服刀架控制。通過對執(zhí)行機構(gòu)建模和分析,設(shè)計出自抗擾控制器。在Matlab仿真試驗中,自抗擾控制在抗干擾性與魯棒性上,均優(yōu)于傳統(tǒng)的PID控制方法。活塞切削實驗結(jié)果表明,應(yīng)用該控制算法,加工精度可達(dá)5/μm。目前,中國的數(shù)控非圓車削機床,加工精度一般在1 0 μm左右,國外進(jìn)口機床加工精度雖然可達(dá)5μm以內(nèi),但價格昂貴。因此,本文進(jìn)行的此項研究,將具有很大的應(yīng)用價值。
-
控制器
+關(guān)注
關(guān)注
112文章
16406瀏覽量
178660 -
仿真
+關(guān)注
關(guān)注
50文章
4102瀏覽量
133755 -
數(shù)控
+關(guān)注
關(guān)注
1文章
286瀏覽量
36128
發(fā)布評論請先 登錄
相關(guān)推薦




 自抗擾控制技術(shù)在非圓數(shù)控車削中的應(yīng)用研究及設(shè)計
自抗擾控制技術(shù)在非圓數(shù)控車削中的應(yīng)用研究及設(shè)計











評論