深度學(xué)習(xí)從入門到放棄？一定是哪里出了問題。

這篇文章想來和你探討下：深度學(xué)習(xí)背后的線性代數(shù)問題。

先做個(gè)簡(jiǎn)單的名詞解釋

深度學(xué)習(xí)：作為機(jī)器學(xué)習(xí)的一個(gè)子域，關(guān)注用于模仿大腦功能和結(jié)構(gòu)的算法：人工神經(jīng)網(wǎng)絡(luò)。

線性代數(shù)：連續(xù)的而不是離散的數(shù)學(xué)形式，許多計(jì)算機(jī)科學(xué)家不太了解它。對(duì)于理解和使

用許多機(jī)器學(xué)習(xí)算法，特別是深度學(xué)習(xí)算法，理解線性代數(shù)是非常重要的。

為什么需要數(shù)學(xué)？

線性代數(shù)，概率和微積分是機(jī)器學(xué)習(xí)用于表述的「語言」。學(xué)習(xí)這些主題將有助于深入理解底層算法機(jī)制，便于開發(fā)新算法。

當(dāng)限定在更小的層次時(shí)，深度學(xué)習(xí)背后的基礎(chǔ)都是數(shù)學(xué)。所以在開始深度學(xué)習(xí)和編程之前，理解基本的線性代數(shù)是至關(guān)重要的。

深度學(xué)習(xí)背后的核心數(shù)據(jù)結(jié)構(gòu)是標(biāo)量，向量，矩陣和張量。讓我們以編程方式用這些解決所有基本的線性代數(shù)問題。

標(biāo)量

標(biāo)量是單個(gè)數(shù)字，是一個(gè) 0 階張量的例子。符號(hào) x∈? 表示 x 是一個(gè)標(biāo)量，屬于一組實(shí)數(shù)值 ?。

深度學(xué)習(xí)有不同的有趣的數(shù)字集合。? 表示正整數(shù)集合（1,2,3，...）。? 表示實(shí)數(shù)，包括正值，負(fù)值和 0。? 表示有理數(shù)的集合，有理數(shù)可以表示為兩個(gè)整數(shù)組成的分?jǐn)?shù)。

Python 中內(nèi)置一些標(biāo)量類型int，float，complex，bytes 和 Unicode。在 NumPy 這個(gè) python 庫中，有 24 種新的基本數(shù)據(jù)類型來描述不同類型的標(biāo)量。有關(guān)數(shù)據(jù)類型的信息，請(qǐng)參閱此處的文檔

（https://docs.scipy.org/doc/numpy-1.14.0/reference/arrays.scalars.html）

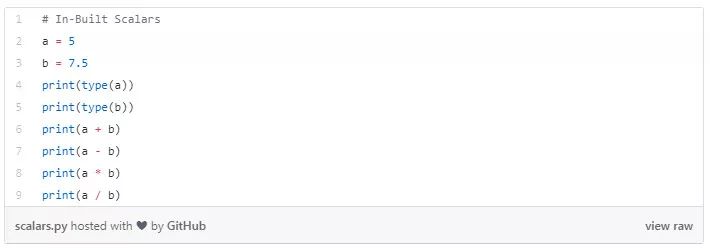
在 Python 中定義標(biāo)量和一些操作：

下面的代碼片段解釋了對(duì)標(biāo)量的幾個(gè)算術(shù)運(yùn)算。

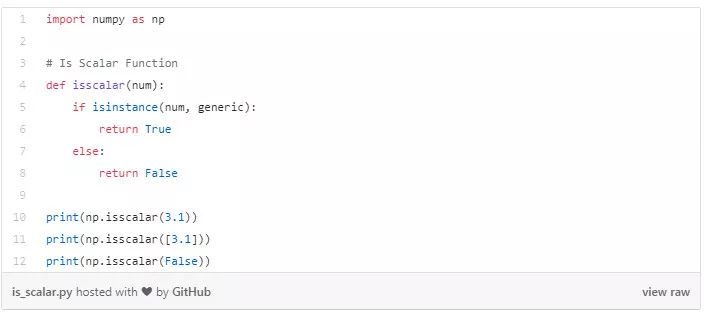
以下代碼片段檢查給定變量是否是標(biāo)量。

向量

向量是一維有序數(shù)組，是一階張量的例子。向量被稱為向量空間的對(duì)象的片段。向量空間可以被認(rèn)為是特定長(zhǎng)度（或維度）的所有可能向量的全部集合。三維實(shí)值向量空間（用 ?^3表示）通常用于從數(shù)學(xué)角度表示我們對(duì)三維空間的現(xiàn)實(shí)世界概念。

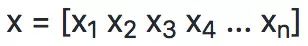
為了明確識(shí)別向量的必要成分，向量的第 i 個(gè)標(biāo)量元素被寫為 x [i]。

在深度學(xué)習(xí)中，向量通常表示特征向量，其原始組成部分定義特定特征的相關(guān)性。這些元素中可能包括二維圖像中像素集強(qiáng)度的相關(guān)重要性或者金融工具的橫截面的歷史價(jià)格值。

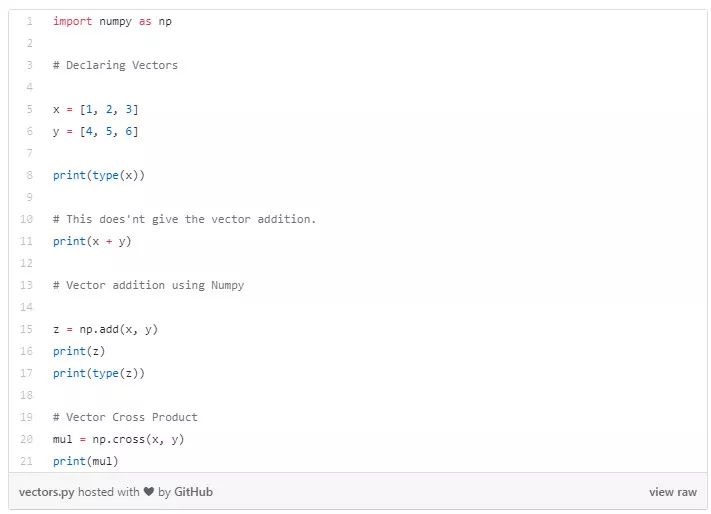
Python 中定義向量和一些操作：

矩陣

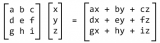
矩陣是由數(shù)字組成的矩形陣列，是二階張量的一個(gè)例子。如果 m 和 n 均為正整數(shù)，即 m, n ∈ ?，則矩陣包含 m 行 n 列，共 m*n 個(gè)數(shù)字。

完整的矩陣可寫為：

將所有矩陣的元素縮寫為以下形式通常很有用。

在 Python 語言中，我們使用 numpy 庫來幫助我們創(chuàng)建 n 維數(shù)組。這些數(shù)組基本上都是矩陣，我們使用矩陣方法通過列表，來定義一個(gè)矩陣。

$python

在 Python 中定義矩陣的操作：

矩陣加法

矩陣可以與標(biāo)量、向量和其他的矩陣相加。這些運(yùn)算都有嚴(yán)格的定義。這些技巧在機(jī)器學(xué)習(xí)和深度學(xué)習(xí)中會(huì)經(jīng)常用到，所以值得熟練運(yùn)用這些技巧。

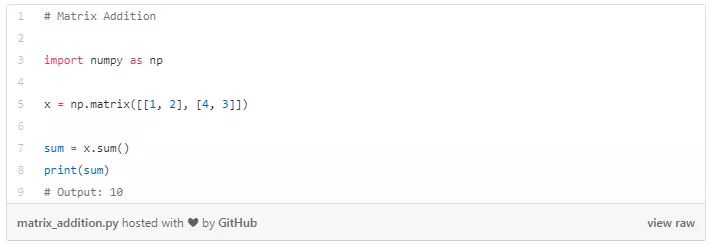
矩陣-矩陣加法

C=A+B（矩陣 A 和 B 應(yīng)該有相同的形狀）

這類方法返回矩陣的形狀，并將兩個(gè)參數(shù)相加后返回這些矩陣的總和。如果這些矩陣的形狀不相同，則程序會(huì)報(bào)錯(cuò)，無法相加。

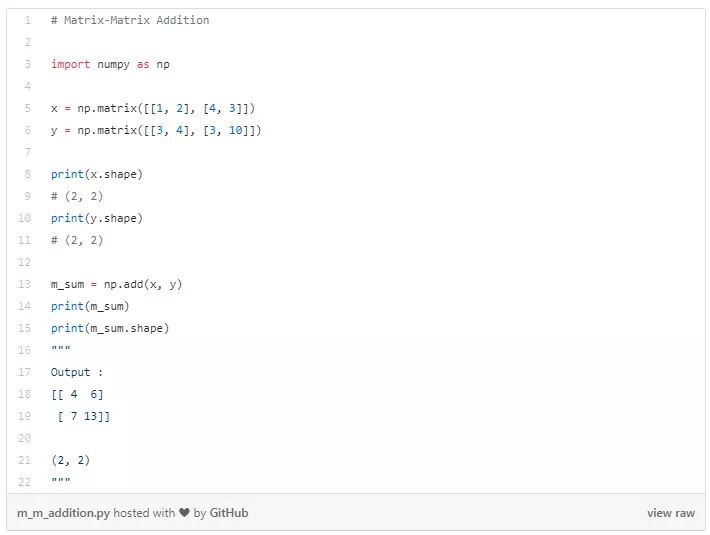
矩陣-標(biāo)量相加

將給定的標(biāo)量加到給定矩陣的所有元素。

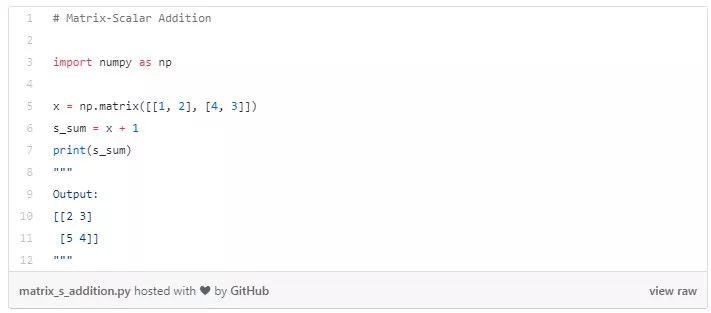
矩陣-標(biāo)量相乘

用給定的標(biāo)量乘以給定矩陣的所有元素。

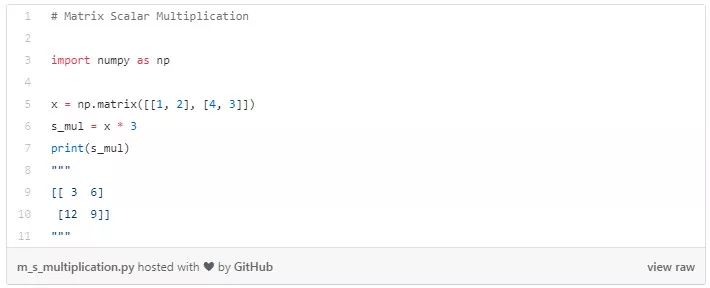
矩陣乘法

矩陣 A 與矩陣 B 相乘得到矩陣 C。

矩陣轉(zhuǎn)置

通過矩陣轉(zhuǎn)置，你可以將行向量轉(zhuǎn)換為列向量，反之亦然。

A=[aij]mxn

AT=[aji]n×m

張量

張量的更一般的實(shí)體封裝了標(biāo)量、向量和矩陣。在物理學(xué)科和機(jī)器學(xué)習(xí)中有時(shí)需要用到高于二階的張量。

我們使用像 tensorflow 或 Pytorch 這樣的 Python 庫來聲明張量，而不是用嵌套矩陣。

在 Pytorch 中定義一個(gè)簡(jiǎn)單的張量:

Python 中張量的幾點(diǎn)算術(shù)運(yùn)算