DeepMind 最近發布了一篇新的論文---《神經算術邏輯單元（NALU）》（https://arxiv.org/abs/1808.00508），這是一篇很有趣的論文，它解決了深度學習中的一個重要問題，即教導神經網絡計算。 令人驚訝的是，盡管神經網絡已經能夠在許多任務，如肺癌分類中獲得卓絕表現，卻往往在一些簡單任務，像計算數字上苦苦掙扎。

在一個展示網絡如何努力從新數據中插入特征的實驗中，我們的研究發現，他們能夠用 -5 到 5 之間的數字將訓練數據分類，準確度近乎完美，但對于訓練數據之外的數字，網絡幾乎無法歸納概括。

論文提供了一個解決方案，分成兩個部分。以下我將簡單介紹一下 NAC 的工作原理，以及它如何處理加法和減法等操作。之后，我會介紹 NALU，它可以處理更復雜的操作，如乘法和除法。 我提供了可以嘗試演示這些代碼的代碼，您可以閱讀上述的論文了解更多詳情。

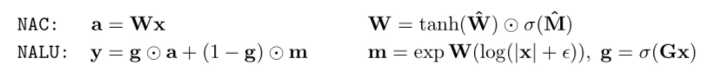
第一神經網絡（NAC）

神經累加器（簡稱 NAC）是其輸入的一種線性變換。什么意思呢？ 它是一個轉換矩陣，是 tanh（W_hat）和 sigmoid（M_hat）的元素乘積。 最后，轉換矩陣 W 乘以輸入（x）。

Python 中的 NAC

1import tensorflow as tf

2

3# NAC

4W_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

5M_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

6

7W = tf.tanh(W_hat) * tf.sigmoid(M_hat)

8# Forward propogation

9a = tf.matmul(in_dim, W)

NAC

第二神經網絡(NALU)

神經算術邏輯單元，或者我們簡稱之為 NALU，是由兩個 NAC 單元組成。 第一個 NAC g 等于 sigmoid（Gx）。 第二個 NAC 在一個等于 exp 的日志空間 m 中運行 (W(log(|x| + epsilon)))

Python 中的 NALU

1import tensorflow as tf

2

3# NALU

4G = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

5

6m = tf.exp(tf.matmul(tf.log(tf.abs(in_dim) + epsilon), W))

7

8g = tf.sigmoid(tf.matmul(in_dim, G))

9

10y = g * a + (1 - g) * m

NALU

通過學習添加來測試 NAC

現在讓我們進行測試，首先將 NAC 轉換為函數。

1# Neural Accumulator

2def NAC(in_dim, out_dim):

3

4in_features = in_dim.shape[1]

5

6# define W_hat and M_hat

7W_hat = tf.get_variable(name = 'W_hat', initializer=tf.initializers.random_uniform(minval=-2, maxval=2),shape=[in_features, out_dim], trainable=True)

8M_hat = tf.get_variable(name = 'M_hat', initializer=tf.initializers.random_uniform(minval=-2, maxval=2), shape=[in_features, out_dim], trainable=True)

9

10W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)

11

12a = tf.matmul(in_dim, W)

13

14return a, W

NAC function in Python

Python 中的 NAC 功能

接下來，讓我們創建一些玩具數據，用于訓練和測試數據。 NumPy 有一個名為 numpy.arrange 的優秀 API，我們將利用它來創建數據集。

1# Generate a series of input number X1 and X2 for training

2x1 = np.arange(0,10000,5, dtype=np.float32)

3x2 = np.arange(5,10005,5, dtype=np.float32)

4

5

6y_train = x1 + x2

7

8x_train = np.column_stack((x1,x2))

9

10print(x_train.shape)

11print(y_train.shape)

12

13# Generate a series of input number X1 and X2 for testing

14x1 = np.arange(1000,2000,8, dtype=np.float32)

15x2 = np.arange(1000,1500,4, dtype= np.float32)

16

17x_test = np.column_stack((x1,x2))

18y_test = x1 + x2

19

20print()

21print(x_test.shape)

22print(y_test.shape)

添加玩具數據

現在，我們可以定義樣板代碼來訓練模型。 我們首先定義占位符 X 和 Y，用以在運行時提供數據。 接下來我們定義的是 NAC 網絡（y_pred，W = NAC（in_dim = X，out_dim = 1））。 對于損失，我們使用 tf.reduce_sum()。 我們將有兩個超參數，alpha，即學習率和我們想要訓練網絡的時期數。在運行訓練循環之前，我們需要定義一個優化器，這樣我們就可以使用 tf.train.AdamOptimizer() 來減少損失。

1# Define the placeholder to feed the value at run time

2X = tf.placeholder(dtype=tf.float32, shape =[None , 2]) # Number of samples x Number of features (number of inputs to be added)

3Y = tf.placeholder(dtype=tf.float32, shape=[None,])

4

5# define the network

6# Here the network contains only one NAC cell (for testing)

7y_pred, W = NAC(in_dim=X, out_dim=1)

8y_pred = tf.squeeze(y_pred)# Remove extra dimensions if any

9

10# Mean Square Error (MSE)

11loss = tf.reduce_mean( (y_pred - Y) **2)

12

13

14# training parameters

15alpha = 0.05 # learning rate

16epochs = 22000

17

18optimize = tf.train.AdamOptimizer(learning_rate=alpha).minimize(loss)

19

20with tf.Session() as sess:

21

22#init = tf.global_variables_initializer()

23cost_history = []

24

25sess.run(tf.global_variables_initializer())

26

27# pre training evaluate

28print("Pre training MSE: ", sess.run (loss, feed_dict={X: x_test, Y:y_test}))

29print()

30for i in range(epochs):

31_, cost = sess.run([optimize, loss ], feed_dict={X:x_train, Y: y_train})

32print("epoch: {}, MSE: {}".format( i,cost) )

33cost_history.append(cost)

34

35# plot the MSE over each iteration

36plt.plot(np.arange(epochs),np.log(cost_history)) # Plot MSE on log scale

37plt.xlabel("Epoch")

38plt.ylabel("MSE")

39plt.show()

40

41print()

42print(W.eval())

43print()

44# post training loss

45print("Post training MSE: ", sess.run(loss, feed_dict={X: x_test, Y: y_test}))

46

47print("Actual sum: ", y_test[0:10])

48print()

49print("Predicted sum: ", sess.run(y_pred[0:10], feed_dict={X: x_test, Y: y_test}))

訓練之后，成本圖的樣子：

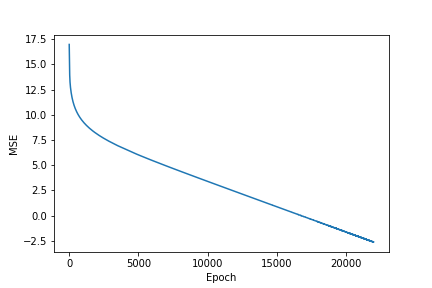
NAC 訓練之后的成本

Actual sum: [2000. 2012. 2024. 2036. 2048. 2060. 2072. 2084. 2096. 2108.]Predicted sum: [1999.9021 2011.9015 2023.9009 2035.9004 2047.8997 2059.8992 2071.8984 2083.898 2095.8975 2107.8967]

雖然 NAC 可以處理諸如加法和減法之類的操作，但是它無法處理乘法和除法。 于是，就有了 NALU 的用武之地。它能夠處理更復雜的操作，例如乘法和除法。

通過學習乘法來測試 NALU

為此，我們將添加片段以使 NAC 成為 NALU。

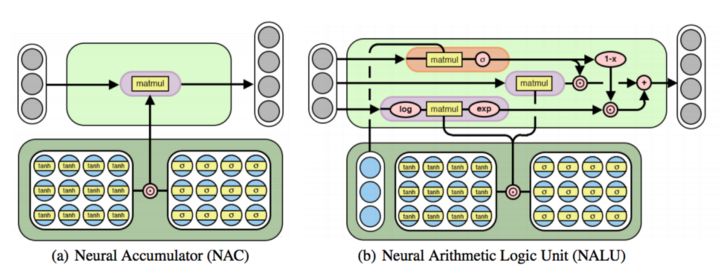
神經累加器（NAC）是其輸入的線性變換。神經算術邏輯單元（NALU）使用兩個帶有綁定的權重的 NACs 來啟用加法或者減法（較小的紫色單元）和乘法/除法（較大的紫色單元），由一個門（橙色單元）來控制。

1# The Neural Arithmetic Logic Unit

2def NALU(in_dim, out_dim):

3

4shape = (int(in_dim.shape[-1]), out_dim)

5epsilon = 1e-7

6

7# NAC

8W_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

9M_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

10G = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

11

12W = tf.tanh(W_hat) * tf.sigmoid(M_hat)

13# Forward propogation

14a = tf.matmul(in_dim, W)

15

16# NALU

17m = tf.exp(tf.matmul(tf.log(tf.abs(in_dim) + epsilon), W))

18g = tf.sigmoid(tf.matmul(in_dim, G))

19y = g * a + (1 - g) * m

20

21return y

Python 中的 NALU 函數

現在，再次創建一些玩具數據，這次我們將進行兩行更改。

1# Test the Network by learning the multiplication

2

3# Generate a series of input number X1 and X2 for training

4x1 = np.arange(0,10000,5, dtype=np.float32)

5x2 = np.arange(5,10005,5, dtype=np.float32)

6

7

8y_train = x1 * x2

9

10x_train = np.column_stack((x1,x2))

11

12print(x_train.shape)

13print(y_train.shape)

14

15# Generate a series of input number X1 and X2 for testing

16x1 = np.arange(1000,2000,8, dtype=np.float32)

17x2 = np.arange(1000,1500,4, dtype= np.float32)

18

19x_test = np.column_stack((x1,x2))

20y_test = x1 * x2

21

22print()

23print(x_test.shape)

24print(y_test.shape)

用于乘法的玩具數據

第 8 行和第 20 行是進行更改的地方，將加法運算符切換為乘法。

現在我們可以訓練的是 NALU 網絡。 我們唯一需要更改的地方是定義 NAC 網絡改成 NALU（y_pred = NALU（in_dim = X，out_dim = 1））。

1# Define the placeholder to feed the value at run time

2X = tf.placeholder(dtype=tf.float32, shape =[None , 2]) # Number of samples x Number of features (number of inputs to be added)

3Y = tf.placeholder(dtype=tf.float32, shape=[None,])

4

5# Define the network

6# Here the network contains only one NAC cell (for testing)

7y_pred = NALU(in_dim=X, out_dim=1)

8y_pred = tf.squeeze(y_pred) # Remove extra dimensions if any

9

10# Mean Square Error (MSE)

11loss = tf.reduce_mean( (y_pred - Y) **2)

12

13

14# training parameters

15alpha = 0.05 # learning rate

16epochs = 22000

17

18optimize = tf.train.AdamOptimizer(learning_rate=alpha).minimize(loss)

19

20with tf.Session() as sess:

21

22#init = tf.global_variables_initializer()

23cost_history = []

24

25sess.run(tf.global_variables_initializer())

26

27# pre training evaluate

28print("Pre training MSE: ", sess.run (loss, feed_dict={X: x_test, Y: y_test}))

29print()

30for i in range(epochs):

31_, cost = sess.run([optimize, loss ], feed_dict={X: x_train, Y: y_train})

32print("epoch: {}, MSE: {}".format( i,cost) )

33cost_history.append(cost)

34

35# Plot the loss over each iteration

36plt.plot(np.arange(epochs),np.log(cost_history)) # Plot MSE on log scale

37plt.xlabel("Epoch")

38plt.ylabel("MSE")

39plt.show()

40

41

42# post training loss

43print("Post training MSE: ", sess.run(loss, feed_dict={X: x_test, Y: y_test}))

44

45print("Actual product: ", y_test[0:10])

46print()

47print("Predicted product: ", sess.run(y_pred[0:10], feed_dict={X: x_test, Y: y_test}))

NALU 訓練后的成本

Actual product: [1000000. 1012032. 1024128. 1036288. 1048512. 1060800. 1073152. 1085568. 1098048. 1110592.]Predicted product: [1000000.2 1012032. 1024127.56 1036288.6 1048512.06 1060800.8 1073151.6 1085567.6 1098047.6 1110592.8 ]

在 TensorFlow 中全面實現