編者按：DRDO研究人員Ayoosh Kathuria深入討論了激活函數如何隱式地改變傳入網絡層的數據分布，進而影響網絡的優化過程。

這是優化系列的第三篇，我們想要通過這一系列文章全面回顧深度學習中的優化技術。到目前為止，我們已經討論了：

用于對抗局部極小值、鞍點的mini batch梯度下降

動量、RMSProp、Adam等方法在原始梯度下降的基礎上加強了哪些方面，以應對病態曲率問題。

分布，該死的分布，還有統計學

不同于之前的機器學習方法，神經網絡并不依賴關于輸入數據的任何概率學或統計學假定。然而，為了確保神經網絡學習良好，最重要的因素之一是傳入神經網絡層的數據需要具有特定的性質。

數據分布應該是零中心化（zero centered）的，也就是說，分布的均值應該在零附近。不具有這一性質的數據可能導致梯度消失和訓練抖動。

分布最好是正態的，否則可能導致網絡過擬合輸入空間的某個區域。

在訓練過程中，不同batch和不同網絡層的激活分布，應該保持一定程度上的一致。如果不具備這一性質，那么我們說分布出現了內部協方差偏移（Internal Covariate shift），這可能拖慢訓練進程。

這篇文章將討論如何使用激活函數應對前兩個問題。文末將給出一些選擇激活函數的建議。

梯度消失

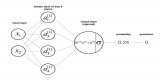
梯度消失問題有豐富的文檔，隨著神經網絡越來越深，這一問題越來越得到重視。下面我們將解釋梯度為什么會消失。讓我們想象一個最簡單的神經網絡，一組線性堆疊的神經元。

實際上，上面的網絡很容易擴展成深度密集連接架構。只需將網絡中的每個神經元替換成一個使用sigmoid激活函數的全連接層。

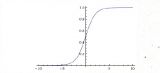
sigmoid函數的圖像是這樣的。

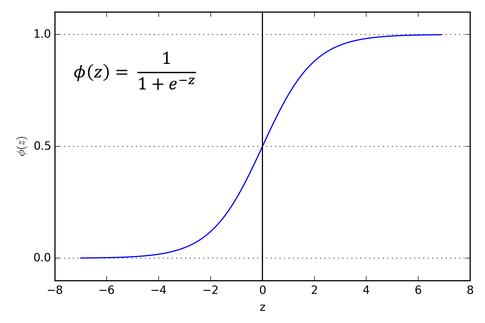
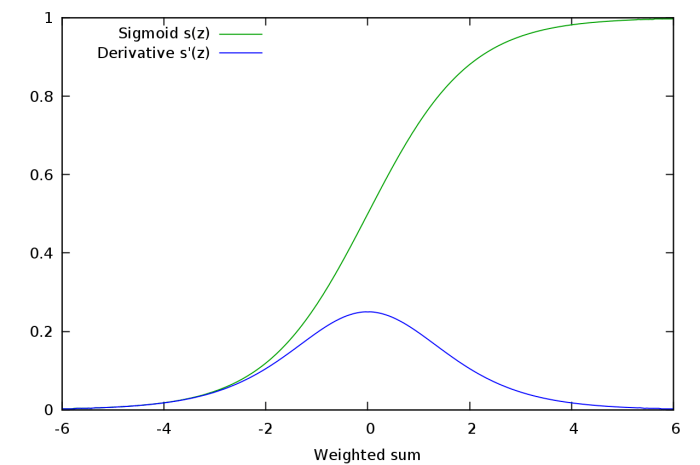
看下sigmoid函數的斜率，我們會發現它在兩端趨向于零。sigmoid函數梯度圖像可以印證這一點。

求sigmoid激活層輸出在其權重上的導數時，我們可以看到，sigmoid函數的梯度是表達式中的一個因子，該梯度的取值范圍為0到1.

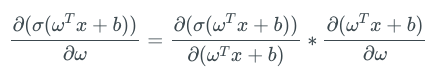
上式中的第二項就是sigmoid的導數，值域為0到1.

回到我們的例子，讓我們求下神經元A的梯度。應用鏈式法則，我們得到：

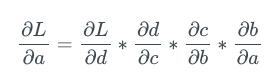
上面的表達式中的每項都可以進一步分解為梯度的乘積，其中一項為sigmoid函數的梯度。例如：

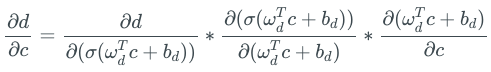
現在，假設A之前不止3個神經元，而是有50個神經元。在實踐中，這完全是可能的，實際應用中的網絡很容易到50層。

那么A的梯度表達式中就包含50項sigmoid梯度的乘積，每項的取值范圍為0到1，這也許會將A的梯度推向零。

讓我們做一個簡單的試驗。隨機取樣50個0到1之間的數，然后將它們相乘。

import random

from functools import reduce

li = [random.uniform(0,1) for x in range(50)

print(reduce(lambda x,y: x*y, li))

你可以自己試驗一下。我試了很多次，從來沒能得到一個數量級大于10-18的數。如果這個值是神經元A的梯度表達式中的一個因子，那么梯度幾乎就等于零。這意味著，在較深的架構中，較深的神經元基本不學習，即使學習，和較淺的網絡層中的神經元相比，學習的速率極低。

這個現象就是梯度消失問題，較深的神經元中的梯度變為零，或者說，消失了。這就導致神經網絡中較深的層學習極為緩慢，或者，在最糟的情況下，根本不學習。

飽和神經元

飽和神經元會導致梯度消失問題進一步惡化。假設，傳入帶sigmoid激活的神經元的激活前數值ωTx + b非常高或非常低。那么，由于sigmoid在兩端處的梯度幾乎是0，任何梯度更新基本上都無法導致權重ω和偏置b發生變化，神經元的權重變動需要很多步才會發生。也就是說，即使梯度原本不低，由于飽和神經元的存在，最終梯度仍會趨向于零。

ReLU救星

在普通深度網絡設定下，ReLU激活函數的引入是緩解梯度消失問題的首個嘗試（LSTM的引入也是為了應對這一問題，不過它的應用場景是循環模型）。

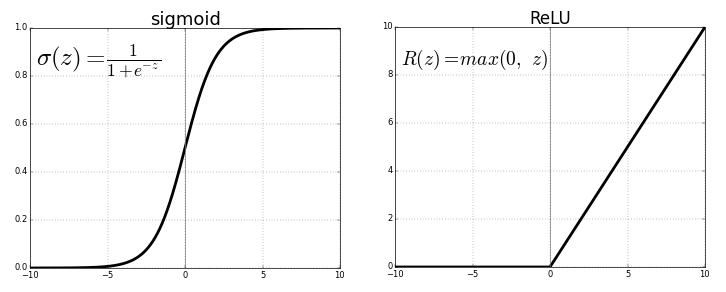
當x > 0時，ReLU的梯度為1，x < 0時，ReLU的梯度為0. 這帶來了一些好處。ReLU函數梯度乘積并不收斂于0，因為ReLU的梯度要么是0，要么是1. 當梯度值為1時，梯度原封不動地反向傳播。當梯度值為0時，從這點往后不會進行反向傳播。

單邊飽和

sigmoid函數是雙邊飽和的，也就是說，正向和負向都趨向于零。ReLU則提供單邊飽和。

準確地說，ReLU的左半部分不叫飽和，飽和的情況下，函數值變動極小，而ReLU的左半部分根本不變。但兩者的作用是類似的。你也許會問，單邊飽和帶來了什么好處？

我們可以把深度網絡中的神經元看成開關，這些開關專門負責檢測特定特征。這些特征常常被稱為概念。高層網絡中的神經元也許最終會專門檢測眼睛、輪胎之類的高層特征，而低層網絡中的神經元最終專門檢測曲線、邊緣之類的低層特征。

當這樣的概念存在于神經網絡的輸入時，我們想要激活相應的神經元，而激活的數量級則可以測量概念的程度。例如，如果神經元檢測到了邊緣，它的數量級也許表示邊緣的銳利程度。

然而，神經元的負值在這里就沒什么意義了。用負值編碼不存在的概念的程度感覺怪怪的。

以檢測邊緣的神經元為例，相比激活值為5的神經元，激活值為10的神經元可能檢測到了更銳利的邊緣。但是區分激活值-5和-10的神經元就沒什么意義了，因為負值表示根本不存在邊緣。因此，統一用零表示概念不存在是很方便的。ReLU的單邊飽和正符合這一點。

信息解纏和對噪聲的魯棒性

單邊飽和提高了神經元對噪聲的魯棒性。為什么？假設神經元的值是無界的，也就是在兩個方向上都不飽和。具有程度不同的概念的輸入產生神經元正值輸出的不同。由于我們想要用數量級指示信號的強度，這很好。

然而，背景噪聲、神經元不擅長檢測的概念（例如，包含弧線的區域傳入檢測線條的神經元），會生成不同的神經元負值輸出。這類不同可能給其他神經元帶去大量無關、無用信息。這也可能導致單元間的相關性。例如，檢測線條的神經元也許和檢測弧線的神經元負相關。

而在神經元單邊飽和（負向）的場景下，噪聲等造成的不同，也就是之前的負值輸出數量級的不同，被激活函數的飽和元素擠壓為零，從而防止噪聲產生無關信號。

稀疏性

ReLU函數在算力上也有優勢。基于ReLU的網絡訓練起來比較快，因為計算ReLU激活的梯度不怎么需要算力，而sigmoid梯度計算就需要指數運算。

ReLU歸零激活前的負值，這就隱式地給網絡引入了稀疏性，同樣節省了算力。

死亡ReLU問題

ReLU也有缺陷。雖然稀疏性在算力上有優勢，但過多的稀疏性實際上會阻礙學習。激活前神經元通常也包含偏置項，如果偏置項是一個過小的負數，使得ωTx + b < 0，那么ReLU激活在反向傳播中的梯度就是0，使負的激活前神經元無法更新。

如果學習到的權重和偏置使整個輸入域上的激活前數值都是負數，那么神經元就無法學習，引起類似sigmoid的飽和現象。這稱為死亡ReLU問題。

零中心化激活

不管輸入是什么，ReLU只輸出非負激活。這可能是一個劣勢。

對基于ReLU的神經網絡而言，網絡層ln的權重ωn的激活為

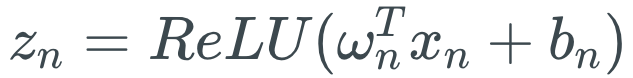
因此，對損失函數L而言：

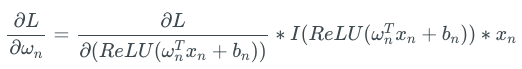
上式中的I是一個指示函數，傳入的ReLU值為正數時輸出1，否則輸出0. 由于ReLU只輸出非負值，ωn中的每項權重的梯度更新正負都一樣。

這有什么問題？問題在于，由于所有神經元的梯度更新的符號都一樣，網絡層ln中的所有權重在一次更新中，要么全部增加，要么全部減少。然而，理想情況的梯度權重更新也許是某些權重增加，另一些權重減少。ReLU下，這做不到。

假設，根據理想的權重更新，有些權重需要減少。然而，如果梯度更新是正值，這些權重可能在當前迭代中變為過大的正值。下一次迭代，梯度可能會變成較小的負值以補償這些增加的權重，這也許會導致最終跳過需要少量負值或正值變動才能取到的權重。

這可能導致搜尋最小值時出現之字模式，拖慢訓練速度。

Leaky ReLU和參數化ReLU

為了克服死亡ReLU問題，人們提出了Leaky ReLU。Leaky ReLU和普通ReLU幾乎完全一樣，除了x < 0時有一個很小的斜率。

在實踐中，這個很小的斜率α通常取0.01.

Leaky ReLU的優勢在于反向傳播可以更新產生負的激活前值的權重，因為Leaky ReLU激活函數的負值區間的梯度是αex。YOLO（點擊閱讀）目標檢測算法就用了Leaky ReLU。

因為負的激活前值會生成負值而不是0，Leaky ReLU沒有ReLU中的權重只在一個方向上更新的問題。

α該取多大，人們做了很多試驗。有一種稱為隨機Leaky ReLU的方法，負值區間的斜率從均值為0、標準差為1的均勻分布中隨機抽取。

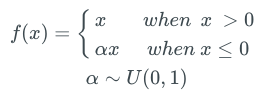
隨機ReLU的論文主張，隨機ReLU能得到比Leaky ReLU更好的結果，訓練起來也更快，并通過經驗方法得出，如果限定只使用單一的α值，那么1/5.5要比通常選擇的0.01效果要好。

隨機Leaky ReLU奏效的原因是負值區間斜率的隨機選擇給負的激活前值梯度帶來了隨機性。在優化算法中引入的隨機性，或者說噪聲，有助于擺脫局部極小值和鞍點（在本系列的第一篇文章中，我們深入討論了這一主題）。

后來人們又進一步提出，α可以看作一個參數，在網絡的訓練過程中學習。采用這一方法的激活函數稱為參數化ReLU。

回顧下飽和

神經元飽和看起來是一件很糟的事情，但ReLU中的單邊飽和未必不好。盡管前面提到的一些ReLU變體抑制了死亡ReLU問題，但卻喪失了單邊飽和的益處。

指數線性單元和偏置偏移

基于上面的討論，看起來一個完美的激活函數應該同時具備以下兩個性質：

產生零中心化分布，以加速訓練過程。

具有單邊飽和，以導向更好的收斂。

Leaky ReLU和PReLU（參數化ReLU）滿足第一個條件，不滿足第二個條件。而原始的ReLU滿足第二個條件，不滿足第一個條件。

同時滿足兩個條件的一個激活函數是指數線性單元（ELU）。

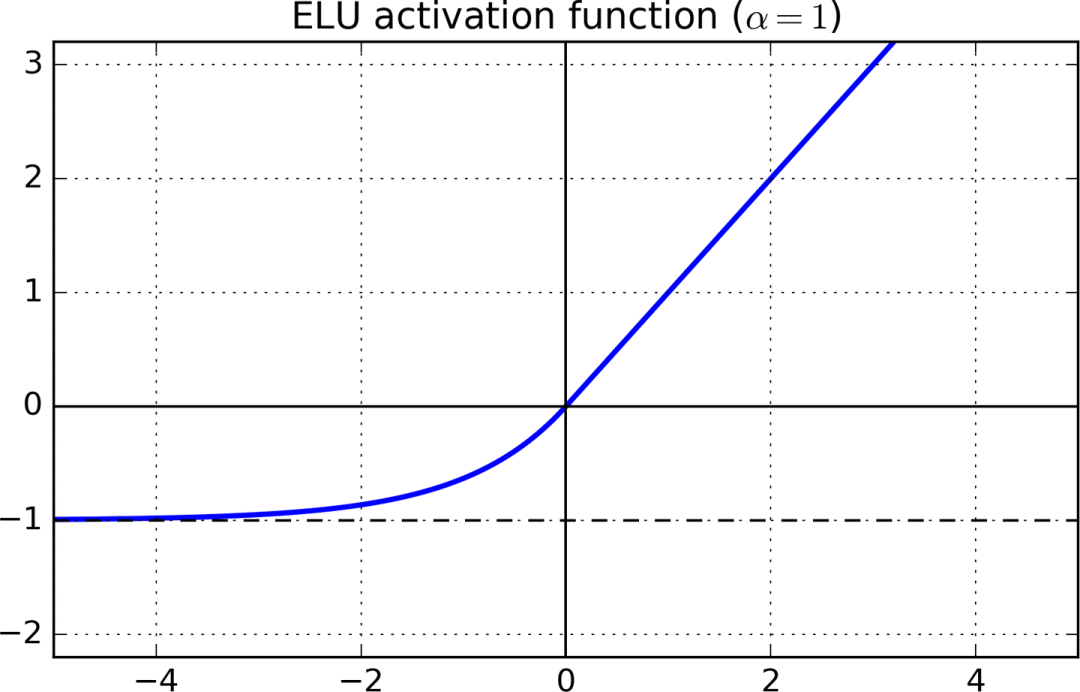
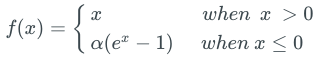
x > 0部分，ELU的梯度是1，x < 0部分的梯度則是α × ex。ELU激活函數的負值區域趨向于-α. α是一個超參數，通常取1.

如何選擇激活函數

首先嘗試ReLU激活。盡管我們上面列出了ReLU的一些問題，但很多人使用ReLU取得了很好的結果。根據奧卡姆剃刀原則，先嘗試更簡單的方案比較好。相比ReLU的有力挑戰者，ReLU的算力負擔最輕。如果你的項目需要從頭開始編程，那么ReLU的實現也特別簡單。

如果ReLU的效果不好，我會接著嘗試Leaky ReLU或ELU。我發現能夠產生零中心化激活的函數一般要比不能做到這點的函數效果好得多。ELU看起來很有吸引力，但是由于負的激活前值會觸發大量指數運算，基于ELU的網絡訓練和推理都很緩慢。如果算力資源對你而言不成問題，或者網絡不是特別巨大，選擇ELU，否則，選擇Leaky ReLU。LReLU和ELU都增加了一個需要調整的超參數。

如果算力資源很充沛，時間很充裕，你可以將上述激活函數的表現與PReLU和隨機ReLU做下對比。如果出現了過擬合，那么隨機ReLU可能會有用。參數化ReLU加入了需要學習的一組參數，所以，只在具備大量訓練數據的情況下才考慮選用參數化ReLU。

結語

這篇文章討論了傳入什么樣的數據分布，有利于神經網絡層恰當地學習。激活函數隱式地歸一化這些分布，而一種稱為批歸一化（Batch Normalization）的技術明確地進行了這一操作。批歸一化是近年來深度學習領域的主要突破之一。不過，我們要到本系列的下一篇文章才會討論這一技術，目前而言，你可以親自嘗試下在自己的網絡上使用不同的激活函數有什么效果！試驗愉快！