前文推送：

數學推導+純Python實現機器學習算法

1：線性回歸

自本系列第一講推出以來，得到了不少同學的反響和贊成，也有同學留言說最好能把數學推導部分寫的詳細點，筆者只能說盡力，因為打公式實在是太浪費時間了。。本節要和大家一起學習的是邏輯（logistic）回歸模型，繼續按照手推公式+純 Python 的寫作套路。

邏輯回歸本質上跟邏輯這個詞不是很搭邊，叫這個名字完全是直譯過來形成的。那該怎么叫呢？其實邏輯回歸本名應該叫對數幾率回歸，是線性回歸的一種推廣，所以我們在統計學上也稱之為廣義線性模型。眾多周知的是，線性回歸針對的是標簽為連續值的機器學習任務，那如果我們想用線性模型來做分類任何可行嗎？答案當然是肯定的。

sigmoid 函數

相較于線性回歸的因變量 y 為連續值，邏輯回歸的因變量則是一個 0/1 的二分類值，這就需要我們建立一種映射將原先的實值轉化為 0/1 值。這時候就要請出我們熟悉的 sigmoid 函數了：

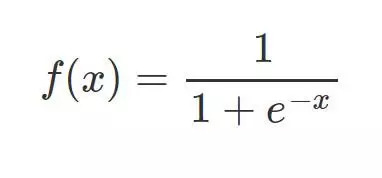
其函數圖形如下：

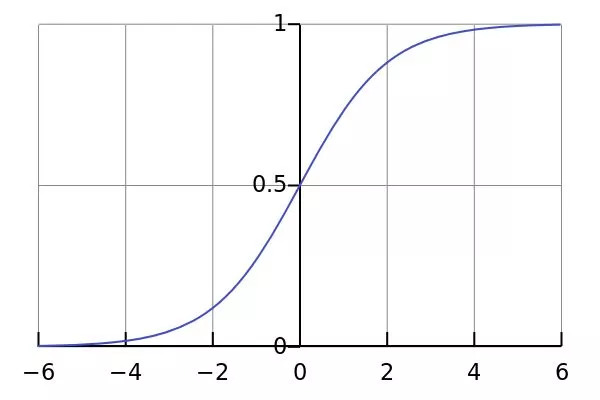
除了長的很優雅之外，sigmoid 函數還有一個很好的特性就是其求導計算等于下式，這給我們后續求交叉熵損失的梯度時提供了很大便利。

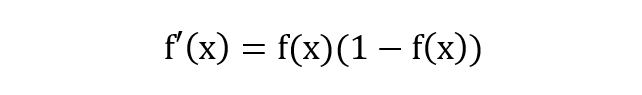
邏輯回歸模型的數學推導

由 sigmoid 函數可知邏輯回歸模型的基本形式為：

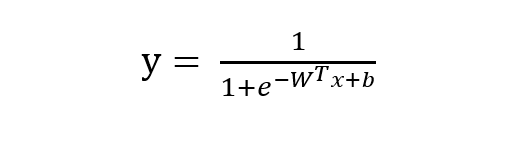
稍微對上式做一下轉換：

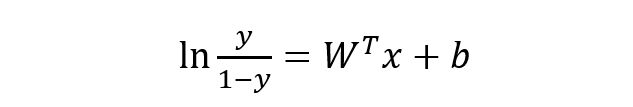
下面將 y 視為類后驗概率 p(y = 1 | x)，則上式可以寫為：

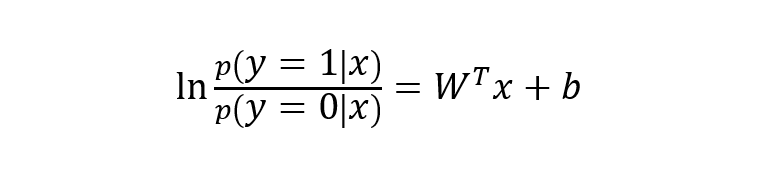
則有：

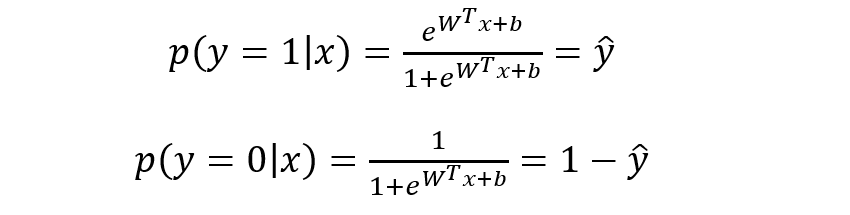
將上式進行簡單綜合，可寫成如下形式：

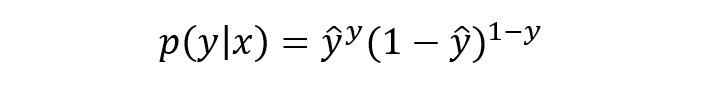
寫成對數形式就是我們熟知的交叉熵損失函數了，這也是交叉熵損失的推導由來：

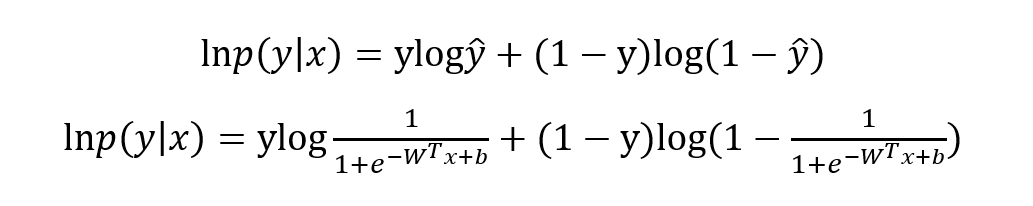
最優化上式子本質上就是我們統計上所說的求其極大似然估計，可基于上式分別關于 W 和b 求其偏導可得：

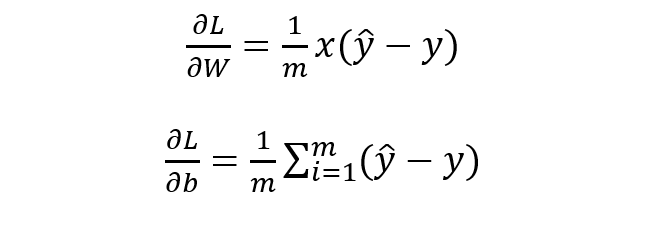
基于 W 和 b 的梯度進行權值更新即可求導參數的最優值，使得損失函數最小化，也即求得參數的極大似然估計，殊途同歸啊。

邏輯回歸的 Python 實現

跟上一講寫線性模型一樣，在實際動手寫之前我們需要理清楚思路。要寫一個完整的邏輯回歸模型我們需要：sigmoid函數、模型主體、參數初始化、基于梯度下降的參數更新訓練、數據測試與可視化展示。

先定義一個 sigmoid 函數：

import numpy as npdef sigmoid(x): z = 1 / (1 + np.exp(-x)) return z

定義模型參數初始化函數：

def initialize_params(dims): W = np.zeros((dims, 1)) b = 0 return W, b

定義邏輯回歸模型主體部分，包括模型計算公式、損失函數和參數的梯度公式：

def logistic(X, y, W, b): num_train = X.shape[0] num_feature = X.shape[1] a = sigmoid(np.dot(X, W) + b) cost = -1/num_train * np.sum(y*np.log(a) + (1-y)*np.log(1-a)) dW = np.dot(X.T, (a-y))/num_train db = np.sum(a-y)/num_train cost = np.squeeze(cost) return a, cost, dW, db

定義基于梯度下降的參數更新訓練過程：

def logistic_train(X, y, learning_rate, epochs): # 初始化模型參數 W, b = initialize_params(X.shape[1]) cost_list = [] # 迭代訓練 for i in range(epochs): # 計算當前次的模型計算結果、損失和參數梯度 a, cost, dW, db = logistic(X, y, W, b) # 參數更新 W = W -learning_rate * dW b = b -learning_rate * db # 記錄損失 if i % 100 == 0: cost_list.append(cost) # 打印訓練過程中的損失 if i % 100 == 0: print('epoch %d cost %f' % (i, cost)) # 保存參數 params = { 'W': W, 'b': b } # 保存梯度 grads = { 'dW': dW, 'db': db } return cost_list, params, grads

定義對測試數據的預測函數：

def predict(X, params): y_prediction = sigmoid(np.dot(X, params['W']) + params['b']) for i in range(len(y_prediction)): if y_prediction[i] > 0.5: y_prediction[i] = 1 else: y_prediction[i] = 0 return y_prediction

使用 sklearn 生成模擬的二分類數據集進行模型訓練和測試：

import matplotlib.pyplot as pltfrom sklearn.datasets.samples_generator import make_classification X,labels=make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=2) rng=np.random.RandomState(2) X+=2*rng.uniform(size=X.shape) unique_lables=set(labels) colors=plt.cm.Spectral(np.linspace(0, 1, len(unique_lables)))for k, col in zip(unique_lables, colors): x_k=X[labels==k] plt.plot(x_k[:, 0], x_k[:, 1], 'o', markerfacecolor=col, markeredgecolor="k", markersize=14) plt.title('data by make_classification()') plt.show()

數據分布展示如下：

對數據進行簡單的訓練集與測試集的劃分：

offset = int(X.shape[0] * 0.9) X_train, y_train = X[:offset], labels[:offset] X_test, y_test = X[offset:], labels[offset:] y_train = y_train.reshape((-1,1)) y_test = y_test.reshape((-1,1)) print('X_train=', X_train.shape) print('X_test=', X_test.shape) print('y_train=', y_train.shape) print('y_test=', y_test.shape)

對訓練集進行訓練：

cost_list, params, grads = lr_train(X_train, y_train, 0.01, 1000)

迭代過程如下：

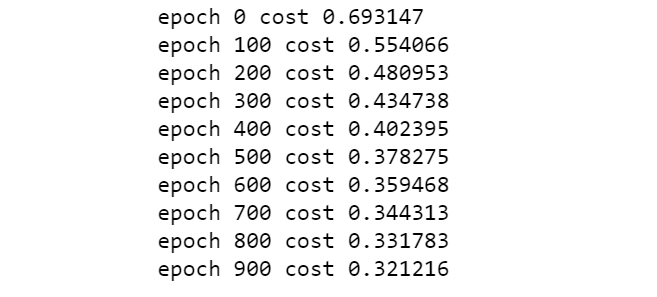
對測試集數據進行預測：

y_prediction = predict(X_test, params) print(y_prediction)

預測結果如下：

定義一個分類準確率函數對訓練集和測試集的準確率進行評估：

def accuracy(y_test, y_pred): correct_count = 0 for i in range(len(y_test)): for j in range(len(y_pred)): if y_test[i] == y_pred[j] and i == j: correct_count +=1 accuracy_score = correct_count / len(y_test) return accuracy_score # 打印訓練準確率accuracy_score_train = accuracy(y_train, y_train_pred) print(accuracy_score_train)

查看測試集準確率：

accuracy_score_test = accuracy(y_test, y_prediction) print(accuracy_score_test)

沒有進行交叉驗證，測試集準確率存在一定的偶然性哈。

最后我們定義個繪制模型決策邊界的圖形函數對訓練結果進行可視化展示：

def plot_logistic(X_train, y_train, params): n = X_train.shape[0] xcord1 = [] ycord1 = [] xcord2 = [] ycord2 = [] for i in range(n): if y_train[i] == 1: xcord1.append(X_train[i][0]) ycord1.append(X_train[i][1]) else: xcord2.append(X_train[i][0]) ycord2.append(X_train[i][1]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcord1, ycord1,s=32, c='red') ax.scatter(xcord2, ycord2, s=32, c='green') x = np.arange(-1.5, 3, 0.1) y = (-params['b'] - params['W'][0] * x) / params['W'][1] ax.plot(x, y) plt.xlabel('X1') plt.ylabel('X2') plt.show() plot_logistic(X_train, y_train, params)

組件封裝成邏輯回歸類

將以上實現過程使用一個 python 類進行封裝：

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets.samples_generator import make_classificationclass logistic_regression(): def __init__(self): pass def sigmoid(self, x): z = 1 / (1 + np.exp(-x)) return z def initialize_params(self, dims): W = np.zeros((dims, 1)) b = 0 return W, b def logistic(self, X, y, W, b): num_train = X.shape[0] num_feature = X.shape[1] a = self.sigmoid(np.dot(X, W) + b) cost = -1 / num_train * np.sum(y * np.log(a) + (1 - y) * np.log(1 - a)) dW = np.dot(X.T, (a - y)) / num_train db = np.sum(a - y) / num_train cost = np.squeeze(cost) return a, cost, dW, db def logistic_train(self, X, y, learning_rate, epochs): W, b = self.initialize_params(X.shape[1]) cost_list = [] for i in range(epochs): a, cost, dW, db = self.logistic(X, y, W, b) W = W - learning_rate * dW b = b - learning_rate * db if i % 100 == 0: cost_list.append(cost) if i % 100 == 0: print('epoch %d cost %f' % (i, cost)) params = { 'W': W, 'b': b } grads = { 'dW': dW, 'db': db } return cost_list, params, grads def predict(self, X, params): y_prediction = self.sigmoid(np.dot(X, params['W']) + params['b']) for i in range(len(y_prediction)): if y_prediction[i] > 0.5: y_prediction[i] = 1 else: y_prediction[i] = 0 return y_prediction def accuracy(self, y_test, y_pred): correct_count = 0 for i in range(len(y_test)): for j in range(len(y_pred)): if y_test[i] == y_pred[j] and i == j: correct_count += 1 accuracy_score = correct_count / len(y_test) return accuracy_score def create_data(self): X, labels = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=2) labels = labels.reshape((-1, 1)) offset = int(X.shape[0] * 0.9) X_train, y_train = X[:offset], labels[:offset] X_test, y_test = X[offset:], labels[offset:] return X_train, y_train, X_test, y_test def plot_logistic(self, X_train, y_train, params): n = X_train.shape[0] xcord1 = [] ycord1 = [] xcord2 = [] ycord2 = [] for i in range(n): if y_train[i] == 1: xcord1.append(X_train[i][0]) ycord1.append(X_train[i][1]) else: xcord2.append(X_train[i][0]) ycord2.append(X_train[i][1]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcord1, ycord1, s=32, c='red') ax.scatter(xcord2, ycord2, s=32, c='green') x = np.arange(-1.5, 3, 0.1) y = (-params['b'] - params['W'][0] * x) / params['W'][1] ax.plot(x, y) plt.xlabel('X1') plt.ylabel('X2') plt.show() if __name__ == "__main__": model = logistic_regression() X_train, y_train, X_test, y_test = model.create_data() print(X_train.shape, y_train.shape, X_test.shape, y_test.shape) cost_list, params, grads = model.logistic_train(X_train, y_train, 0.01, 1000) print(params) y_train_pred = model.predict(X_train, params) accuracy_score_train = model.accuracy(y_train, y_train_pred) print('train accuracy is:', accuracy_score_train) y_test_pred = model.predict(X_test, params) accuracy_score_test = model.accuracy(y_test, y_test_pred) print('test accuracy is:', accuracy_score_test) model.plot_logistic(X_train, y_train, params)

好了，關于邏輯回歸的內容，筆者就介紹到這，至于如何在實戰中檢驗邏輯回歸的分類效果，還需各位親自試一試。多說一句，邏輯回歸模型與感知機、神經網絡和深度學習有著千絲萬縷的關系，作為基礎的機器學習模型，希望大家能夠牢固掌握其數學推導和手動實現方式，在此基礎上再去調用 sklearn 中的 LogisticRegression 模塊，必能必能裨補闕漏，有所廣益。