編者按:DRDO研究人員Ayoosh Kathuria深入介紹了批歸一化的概念,終結了廣泛流傳的批歸一化降低內部協方差偏移的流言。
認出上面的人了嗎?這是探索頻道的《留言終結者》。
今天,我們也要分辨一下,批歸一化到底能不能解決內部協方差偏移的問題?盡管批歸一化(Batch Normalization)提出已經有一些年了,已經成為深度架構的主要部件,它仍然是深度學習中最容易誤解的概念之一。
批歸一化真的可以解決內部協方差偏移問題?如果不能解決,那它的作用是什么?你所接受的整個深度學習教育是一個謊言嗎?讓我們來尋找答案吧!
開始之前……
我想提醒一下,本文是深度學習優化算法系列的第四篇,前三篇文章討論了:
隨機梯度下降如何克服深度學習中的局部極小值和鞍點問題?
動量和Adam等方法如何加強原始梯度下降,以應對優化曲面上的病態曲率問題?
如何使用不同的激活函數處理梯度消失問題?
上一篇文章中,我們學到的一點是,為了讓神經網絡高效學習,傳入網絡層的輸入應該大致符合:
零中心化
不同batch和不同網絡層的數據分布,應保持一定程度上的一致
第二個條件的一種反例是epoch和epoch間的分布劇烈變動。
內部協方差偏移
批歸一化的論文題為Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift(批歸一化:通過降低內部協方差偏移加速深度網絡訓練),從標題就可以看出,這篇論文的假定是批歸一化可以解決內部協方差偏移的問題。
那么,內部協方差偏移,簡稱ICS,到底是什么?ICS指神經網絡層間的輸入分布搖擺不定。內部指這種搖擺不定發生在神經網絡的中間層(視作網絡的內部)。協方差指以權重為參數的分布在網絡層之間的差異。偏移指分布在改變。
讓我們嘗試描述下事情是怎么發生的。同樣,想象一個盡可能簡單的網絡,線性堆疊的神經元,你可以通過用網絡層替換神經元來擴展這一類比。
假設我們優化上述網絡的損失函數L,那么神經元d的權重ωd的更新規則為:
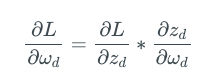
這里,zd= ωdzc,為神經元d的激活值。因此,上式可以化簡為:
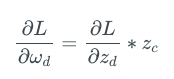
所以,我們看到,網絡層d的權重的梯度取決于網絡層c的輸出。神經網絡中的每一層同理。神經元的權重梯度取決于它的輸入,即后一層的輸出。
接著,梯度反向傳播,權重更新,這一過程不斷重復。現在,讓我們回到網絡層d.
由于我們在d上進行了梯度更新,我們現在期望ωd能得到更低的損失。然而結果也許不符合我們的期望。為什么?讓我們仔細看下。
我們在迭代i時進行了初次更新,讓我們將此時c在迭代i的輸出分布記為pci。現在,d的更新假定輸入為pci。
然而,在反向傳播階段,c的權重ωc也得到了更新。這導致c的輸出分布發生了偏移。
假設在下一次迭代i+1中,zc的分布偏移至pci+1。由于網絡層d的權重之前是根據pci更新的,但現在網絡層d面臨的輸入分布卻是pci+1。這一顯著差異可能導致網絡層生成的輸出損失不下降。
現在,我們有兩個問題。
為什么輸入分布偏移讓網絡層更難學習?
這個偏移是否大到足以導致上面描述的場景?
我們先回答第一個問題。
為什么內部協方差偏移會成為問題?
神經網絡所做的是生成輸入x到輸出y之間的映射f。為什么x的分布改變會造成問題?
例如,假設x從正態分布
變為非正態分布:
假設我們嘗試擬合的映射是f = 2x. 那x分布的密度向左偏移,還是均勻散布,又有什么區別?
然而,由于神經網絡,更準確的說,現代的深度網絡是極為強大的曲線擬合器,這樣的分布偏移確實有影響。正像《蜘蛛俠》所言:“能力越大,責任越大。”
假設網絡層l面對的x有著如下圖所示的分布,并且,到目前為止,通過訓練,網絡層學習到的函數可以用下圖中的虛線表示。
現在,假設梯度更新后,下一個minibatch的x分布變化了:
注意到沒有?和之前相比,這一mini-batch的損失變大了。
讓我們回過頭去看原先的圖形。如你所見,我們原本學習的映射f在降低前一個mini-batch的損失方面做的不錯。同樣,還有許多其他函數在這方面的表現也不錯。
如果我們當初選擇的是紅色虛線,那么下一mini-batch的損失也不會大。
很明顯,現在我們需要回答的問題是如何修改算法,使得我們最終學習到紅色虛線而不是黑色虛線?簡單的回答是,這個問題不存在簡單的答案。在這一點上,與其嘗試找到解決這類情況的方案,不如集中精力避免這類情況發生。
ICS最終擾亂學習的原因是神經網絡總是在輸入分布的稠密區表現較好。稠密區的數據點的損失下降得更多,因為稠密區的數據點統治了平均損失,而我們試圖最小化的正是平均損失。
然而,如果在訓練期間ICS最終改變了后續batch的輸入分布的稠密區,那么網絡從之前的迭代中學到的權重就不再是最優的了。這大概需要非常小心地調整超參數才能合理地學習。這解釋了為什么ICS可能造成問題。
當然,mini-batch內部還是要有適當差異的。差異可以確保映射沒有過度擬合輸入分布的單個區域。另外,我們也想要輸入的均值在零左右,原因詳見本系列的上一篇文章。
歸一化輸入
應對這一問題的一種方法是歸一化神經網絡的輸入,使輸入分布均值為零,方差為單位方差。然而,只有當網絡不夠深的時候這個方法才有效果。當網絡變得越來越深,例如,20層以上,即使輸入經過了歸一化,20多層權重的微小波動可能造成深層輸入分布的巨大改變。
一個不太正確的類比是語言的變化。隨著我們旅行距離的增加,語言也發生了變化。然而,距離較近的地方,語言有很多相似性。比如,西班牙語和葡萄牙語。這兩種語言都源自原始印歐語。然而,8000公里之外的印度人說的印度斯坦語,同樣源自原始印歐語,和西班牙的差別卻遠大于西班牙語和葡萄牙語的差別。原因是短距離內的微小變動隨著距離的增加而逐漸放大。深度網絡同理。
進入批歸一化
現在我們介紹批歸一化(BN)的概念,BN歸一化網絡層的激活輸出,同時進行了其他一些操作。
上面的公式描述了批歸一化層做了什么。等式2-4描述了mini-batch間的激活的均值、方差是如何計算的,以及通過減去均值除以標準差歸一化分布。
等式5是關鍵部分。γ和β是所謂的批歸一化層的參數,等式5的輸出均值為β,標準差為γ。從效果上說,批歸一化層有助于優化算法控制網絡層輸出的均值和方差。
ICS袪魅
引入批歸一化的論文將批歸一化的成功歸功于擺脫了內部協方差偏移。然而,這是一個荒謬的陳述,批歸一化根本沒有防止ICS。
內部協方差偏移是指網絡訓練過程中輸入分布的改變。批歸一化的參數γ和β是為了調整激活的均值和方差。然而,這意味著這兩個參數是可訓練的,也就是是說,將隨著訓練的進行而改變,那么批歸一化自身就會導致激活分布的改變,也就是內部協方差偏移。如果它防止了內部協方差偏移,參數γ和β毫無意義。
為何批歸一化有效?
既然批歸一化沒能克服內部協方差偏移,那么批歸一化是怎么起效的呢?
GAN之父Ian Goodfellow曾經在一個講座中提出過一種可能的解釋(講座的網址見文末)。我必須提醒你注意,到目前為止,盡管來自深度學習的權威,這仍然只是一項未經證明的猜測。
Goodfellow認為原因在于批歸一化層的兩個參數。
讓我們再次考慮之前的超級簡單的玩具網絡。
這里,當我們更新a的權重的時候,僅僅計算?L/?a,即損失函數在a上的反應。然而,我們沒有考慮改變a的權重同時也將改變后續層b、c、d的輸出。
這實際上是因為算力限制,我們無法利用二階以上的優化方法。梯度下降及其變體只能捕捉一階交互(我們在本系列的第二篇文章中深入討論了這一點)。
深度神經網絡具有高階交互,這意味著改變某一層的權重也許會在損失函數之外影響其他層的統計特征。如果不考慮這樣的跨層交互,就會產生內部協方差偏移。每次更新一個網絡層的權重,都有可能對之后的網絡層的統計特征造成不利影響。
在這樣的情形下,可能需要精心的初始化、超參數調整、長時間的訓練才能收斂。然而,當我們在層間添加批歸一化層之后,網絡層的統計特征只受γ、β這兩個參數的影響。
現在,優化算法只需調整兩個參數即可控制任意層的統計特征,而不需要調整之前層的所有權重。這大大加速了收斂,并免去了精心初始化和超參數調整的需要。因此,批歸一化更多地起到設置檢查點的作用。
注意,具備任意設定網絡層的均值和標準差的能力同時意味著我們可以恢復原分布,如果恢復原分布足以使訓練正常的話。
在激活前還是激活后進行批歸一化
盡管原始論文在激活函數之前應用批歸一化,在實踐中發現在激活之后應用批歸一化能得到更好的結果。這看起來很有道理,因為如果我們在批歸一化之后放置激活,那么由于批歸一化層的輸出還需要經過激活,批歸一化就無法完全控制下一層的輸入。
推理階段的批歸一化
在推理階段使用批歸一化有一定技巧性。這是因為在推理階段我們不一定有批次可言。例如,進行實時目標檢測時,每次只處理一幀,并不存在批次。
而沒有批次,我們就無法計算均值和方差,也就無法得到批歸一化層的輸出。在這一情形下,我們維持一個訓練階段的均值、方差的移動平均,然后在推理階段使用這一移動平均。這是大多數自帶批歸一化層的深度學習庫的做法。
這一做法的依據是大數定律。在樣本足夠的的情況下,批統計量趨向于收斂至真實統計量。移動平均也有助于消除mini batch自帶的噪聲。
如果測試階段可以使用批次,那么我們使用和上文提到的幾乎一模一樣的公式,只有一處例外。我們不使用
而使用如下公式:
為何分母使用m-1而不是m是因為均值已經是我們估計的,mini batch中只有m-1個項獨立觀測了。用術語來說,就是自由度只有m-1,具體細節的討論超出了本文的范圍。
起正則作用的批歸一化
批歸一化同時也起到了正則化的作用。相比真實均值和方差,為每個批次估計的均值和方差是一個加噪的版本,這給優化搜索過程引入了隨機性,從而起到了正則化的作用。
結語
盡管批歸一化已經成為當今深度架構的標準元素,直到最近研究方向才轉向理解批歸一化到底為何有效。最近受到很多關注的一篇論文,直接以How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift)為題(批歸一化如何幫助優化?不,它和內部協方差偏移無關)。這篇論文揭示了,和沒有使用批歸一化的網絡相比,批歸一化實際上增加了內部協方差。論文的主要洞見在于,批歸一化平滑了損失曲面,所以批歸一化才這么有效。2017年,有人提出了SELU(擴展指數線性激活單元)激活函數,隱式地歸一化其激活(批歸一化顯式地進行了這一點)。SELU的原論文包含100頁數學精確說明這一切是如何發生的,偏愛數學的讀者應該讀一下。
優化是深度學習中一個激動人心的領域。這些年來,許多深度學習應用得到了加強,已經可以實用,但直到最近我們才開始探索誘人的深度學習理論部分。
最后,讓我們說……流言終結!
進一步閱讀
批歸一化論文:https://arxiv.org/abs/1502.03167
How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift): https://arxiv.org/abs/1805.11604
擴展指數線性激活單元論文:https://arxiv.org/abs/1706.02515
Ian Goodfellow關于批歸一化的講座:https://youtu.be/Xogn6veSyxA
Reddit上關于把批歸一化放在ReLU前面還是后面的討論:https://www.reddit.com/comments/67gonq/
-
神經網絡
+關注
關注
42文章
4814瀏覽量
103832 -
深度學習
+關注
關注
73文章
5562瀏覽量
122856
原文標題:優化算法入門:四、批歸一化揭秘
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
Matlab協方差矩陣的計算原理
Matlab協方差矩陣的計算原理
基于協方差矩陣特征分解的多通道SAR-GMTI方法及性能分析
基于雜波協方差矩陣特征向量分析STAP降維方法
基于稀疏干擾協方差矩陣重構的穩健自適應波束形成算法(CAPON譜改正)
協方差公式_協方差的計算公式例子

協方差矩陣是什么_協方差矩陣計算公式_如何計算協方差矩陣

基于協方差矩陣降維稀疏表示的二維波達方向估計方法



















評論