今天和大家講講,在做算法題時(shí)常用的一些技巧。對(duì)于平時(shí)沒(méi)用過(guò)這些技巧的人,或許你可以考慮試著去看看在實(shí)踐中能否用的上這些技巧來(lái)優(yōu)化問(wèn)題的解。
1. 巧用數(shù)組下標(biāo)
數(shù)組的下標(biāo)是一個(gè)隱含的很有用的數(shù)組,特別是在統(tǒng)計(jì)一些數(shù)字,或者判斷一些整型數(shù)是否出現(xiàn)過(guò)的時(shí)候。例如,給你一串字母,讓你判斷這些字母出現(xiàn)的次數(shù)時(shí),我們就可以把這些字母作為下標(biāo),在遍歷的時(shí)候,如果字母a遍歷到,則arr[a]就可以加1了,即 arr[a]++;
通過(guò)這種巧用下標(biāo)的方法,我們不需要逐個(gè)字母去判斷。
我再舉個(gè)例子:
問(wèn)題:給你n個(gè)無(wú)序的int整型數(shù)組arr,并且這些整數(shù)的取值范圍都在0-20之間,要你在 O(n) 的時(shí)間復(fù)雜度中把這 n 個(gè)數(shù)按照從小到大的順序打印出來(lái)。
對(duì)于這道題,如果你是先把這 n 個(gè)數(shù)先排序,再打印,是不可能O(n)的時(shí)間打印出來(lái)的。但是數(shù)值范圍在 0-20。我們就可以巧用數(shù)組下標(biāo)了。把對(duì)應(yīng)的數(shù)值作為數(shù)組下標(biāo),如果這個(gè)數(shù)出現(xiàn)過(guò),則對(duì)應(yīng)的數(shù)組加1。
代碼如下:
public void f(int arr[]) { int[] temp = new int[21]; for (int i = 0; i < arr.length; i++) { ? ? ? ? ? ?temp[arr[i]]++; ? ? ? ?} ? ? ? ?//順序打印 ? ? ? ?for (int i = 0; i < 21; i++) { ? ? ? ? ? ?for (int j = 0; j < temp[i]; j++) { ? ? ? ? ? ? ? ?System.out.println(i); ? ? ? ? ? ?} ? ? ? ?} ? ?}
提醒:可以左右滑動(dòng)
利用數(shù)組下標(biāo)的應(yīng)用還有很多,大家以后在遇到某些題的時(shí)候可以考慮是否可以巧用數(shù)組下標(biāo)來(lái)優(yōu)化。
2. 巧用取余
有時(shí)候我們?cè)诒闅v數(shù)組的時(shí)候,會(huì)進(jìn)行越界判斷,如果下標(biāo)差不多要越界了,我們就把它置為0重新遍歷。特別是在一些環(huán)形的數(shù)組中,例如用數(shù)組實(shí)現(xiàn)的隊(duì)列。往往會(huì)寫(xiě)出這樣的代碼:
for (int i = 0; i < N; i++) { ? ? ? ?if (pos < N) { ? ? ? ? //沒(méi)有越界 ? ? ? ? // 使用數(shù)組arr[pos]? ? ? ? else {? ? ? ? ? pos = 0;//置為0再使用數(shù)組 ? ? ? ? ? //使用arr[pos]? ? ? ? ?}? ? ? ? pos++;? ?}
實(shí)際上我們可以通過(guò)取余的方法來(lái)簡(jiǎn)化代碼
for (int i = 0; i < N; i++) { ? //使用數(shù)組arr[pos] ? (我們假設(shè)剛開(kāi)始的時(shí)候pos < N) ? pos = (pos + 1) % N;}
3. 巧用雙指針
對(duì)于雙指針,在做關(guān)于單鏈表的題是特別有用,比如“判斷單鏈表是否有環(huán)”、“如何一次遍歷就找到鏈表中間位置節(jié)點(diǎn)”、“單鏈表中倒數(shù)第 k 個(gè)節(jié)點(diǎn)”等問(wèn)題。對(duì)于這種問(wèn)題,我們就可以使用雙指針了,會(huì)方便很多。我順便說(shuō)下這三個(gè)問(wèn)題怎么用雙指針解決吧。
例如對(duì)于第一個(gè)問(wèn)題
我們就可以設(shè)置一個(gè)慢指針和一個(gè)快指針來(lái)遍歷這個(gè)鏈表。慢指針一次移動(dòng)一個(gè)節(jié)點(diǎn),而快指針一次移動(dòng)兩個(gè)節(jié)點(diǎn),如果該鏈表沒(méi)有環(huán),則快指針會(huì)先遍歷完這個(gè)表,如果有環(huán),則快指針會(huì)在第二次遍歷時(shí)和慢指針相遇。
對(duì)于第二個(gè)問(wèn)題
一樣是設(shè)置一個(gè)快指針和慢指針。慢的一次移動(dòng)一個(gè)節(jié)點(diǎn),而快的兩個(gè)。在遍歷鏈表的時(shí)候,當(dāng)快指針遍歷完成時(shí),慢指針剛好達(dá)到中點(diǎn)。
對(duì)于第三個(gè)問(wèn)題
設(shè)置兩個(gè)指針,其中一個(gè)指針先移動(dòng)k個(gè)節(jié)點(diǎn)。之后兩個(gè)指針以相同速度移動(dòng)。當(dāng)那個(gè)先移動(dòng)的指針遍歷完成的時(shí)候,第二個(gè)指針正好處于倒數(shù)第k個(gè)節(jié)點(diǎn)。
你看,采用雙指針?lè)奖愣嗔税伞K砸院笤谔幚砼c鏈表相關(guān)的一些問(wèn)題的時(shí)候,可以考慮雙指針哦。
4. 巧用移位運(yùn)算。
有時(shí)候我們?cè)谶M(jìn)行除數(shù)或乘數(shù)運(yùn)算的時(shí)候,例如n / 2,n / 4, n / 8這些運(yùn)算的時(shí)候,我們就可以用移位的方法來(lái)運(yùn)算了,這樣會(huì)快很多。
例如:
n / 2 等價(jià)于 n >> 1
n / 4 等價(jià)于 n >> 2
n / 8 等價(jià)于 n >> 3。
這樣通過(guò)移位的運(yùn)算在執(zhí)行速度上是會(huì)比較快的,也可以顯的你很厲害的樣子,哈哈。
還有一些 &(與)、|(或)的運(yùn)算,也可以加快運(yùn)算的速度。例如判斷一個(gè)數(shù)是否是奇數(shù),你可能會(huì)這樣做
if(n % 2 == 1){ dosomething();}
不過(guò)我們用與或運(yùn)算的話(huà)會(huì)快很多。例如判斷是否是奇數(shù),我們就可以把n和1相與了,如果結(jié)果為1,則是奇數(shù),否則就不會(huì)。即
if(n & 1 == 1){ dosomething();)
具體的一些運(yùn)算技巧,還得需要你們多在實(shí)踐中嘗試著去使用,這樣用久后就會(huì)比較熟練了。
5. 設(shè)置哨兵位
在鏈表的相關(guān)問(wèn)題中,我們經(jīng)常會(huì)設(shè)置一個(gè)頭指針,而且這個(gè)頭指針是不存任何有效數(shù)據(jù)的,只是為了操作方便,這個(gè)頭指針我們就可以稱(chēng)之為哨兵位了。
例如我們要?jiǎng)h除頭第一個(gè)節(jié)點(diǎn)是時(shí)候,如果沒(méi)有設(shè)置一個(gè)哨兵位,那么在操作上,它會(huì)與刪除第二個(gè)節(jié)點(diǎn)的操作有所不同。但是我們?cè)O(shè)置了哨兵,那么刪除第一個(gè)節(jié)點(diǎn)和刪除第二個(gè)節(jié)點(diǎn)那么在操作上就一樣了,不用做額外的判斷。當(dāng)然,插入節(jié)點(diǎn)的時(shí)候也一樣。
有時(shí)候我們?cè)诓僮鲾?shù)組的時(shí)候,也是可以設(shè)置一個(gè)哨兵的,把a(bǔ)rr[0]作為哨兵。例如,要判斷兩個(gè)相鄰的元素是否相等時(shí),設(shè)置了哨兵就不怕越界等問(wèn)題了,可以直接arr[i] == arr[i-1]?了。不用怕i = 0時(shí)出現(xiàn)越界。
當(dāng)然我這只是舉一個(gè)例子,具體的應(yīng)用還有很多,例如插入排序,環(huán)形鏈表等。
6. 與遞歸有關(guān)的一些優(yōu)化
(1).對(duì)于可以遞歸的問(wèn)題考慮狀態(tài)保存
當(dāng)我們使用遞歸來(lái)解決一個(gè)問(wèn)題的時(shí)候,容易產(chǎn)生重復(fù)去算同一個(gè)子問(wèn)題,這個(gè)時(shí)候我們要考慮狀態(tài)保存以防止重復(fù)計(jì)算。例如我隨便舉一個(gè)之前舉過(guò)的問(wèn)題
問(wèn)題:一只青蛙一次可以跳上1級(jí)臺(tái)階,也可以跳上2級(jí)。求該青蛙跳上一個(gè)n級(jí)的臺(tái)階總共有多少種跳法?
這個(gè)問(wèn)題用遞歸很好解決。假設(shè) f(n) 表示n級(jí)臺(tái)階的總跳數(shù)法,則有
f(n) = f(n-1) + f(n - 2)。
遞歸的結(jié)束條件是當(dāng)0 <= n <= 2時(shí), f(n) = n。因此我們可以很容易寫(xiě)出遞歸的代碼
public int f(int n) { if (n <= 2) { ? ? ? ? ? ?return n; ? ? ? ?} else { ? ? ? ? ? ?return f(n - 1) + f(n - 2); ? ? ? ?} ? ?}
不過(guò)對(duì)于可以使用遞歸解決的問(wèn)題,我們一定要考慮是否有很多重復(fù)計(jì)算。顯然對(duì)于 f(n) = f(n-1) + f(n-2) 的遞歸,是有很多重復(fù)計(jì)算的。如
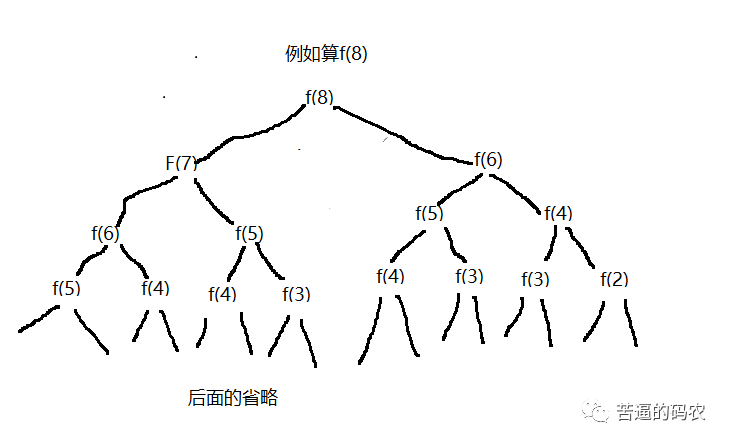
就有很多重復(fù)計(jì)算了。這個(gè)時(shí)候我們要考慮狀態(tài)保存。例如用hashMap來(lái)進(jìn)行保存,當(dāng)然用一個(gè)數(shù)組也是可以的,這個(gè)時(shí)候就像我們上面說(shuō)的巧用數(shù)組下標(biāo)了。可以當(dāng)arr[n] = 0時(shí),表示n還沒(méi)計(jì)算過(guò),當(dāng)arr[n] != 0時(shí),表示f(n)已經(jīng)計(jì)算過(guò),這時(shí)就可以把計(jì)算過(guò)的值直接返回回去了。因此我們考慮用狀態(tài)保存的做法代碼如下:
//數(shù)組的大小根據(jù)具體情況來(lái),由于int數(shù)組元素的的默認(rèn)值是0 //因此我們不用初始化 int[] arr = new int[1000]; public int f(int n) { if (n <= 2) { ? ? ? ? ? ?return n; ? ? ? ?} else { ? ? ? ? ? ?if (arr[n] != 0) { ? ? ? ? ? ? ? ?return arr[n];//已經(jīng)計(jì)算過(guò),直接返回 ? ? ? ? ? ?} else { ? ? ? ? ? ? ? ?arr[n] = f(n-1) + f(n-2); ? ? ? ? ? ? ? ?return arr[n]; ? ? ? ? ? ?} ? ? ? ?} ? ?}
這樣,可以極大著提高算法的效率。也有人把這種狀態(tài)保存稱(chēng)之為備忘錄法。
(2).考慮自底向上
對(duì)于遞歸的問(wèn)題,我們一般都是從上往下遞歸的,直到遞歸到最底,再一層一層著把值返回。
不過(guò),有時(shí)候當(dāng)n比較大的時(shí)候,例如當(dāng) n = 10000時(shí),那么必須要往下遞歸10000層直到 n <=2 才將結(jié)果慢慢返回,如果n太大的話(huà),可能棧空間會(huì)不夠用。
對(duì)于這種情況,其實(shí)我們是可以考慮自底向上的做法的。例如我知道
f(1) = 1;
f(2) = 2;
那么我們就可以推出f(3) = f(2) + f(1) = 3。從而可以推出f(4),f(5)等直到f(n)。因此,我們可以考慮使用自底向上的方法來(lái)做。
代碼如下:
public int f(int n) { if(n <= 2) ? ? ? ? ? ?return n; ? ? ? ?int f1 = 1; ? ? ? ?int f2 = 2; ? ? ? ?int sum = 0; ? ? ? ?for (int i = 3; i <= n; i++) { ? ? ? ? ? ?sum = f1 + f2; ? ? ? ? ? ?f1 = f2; ? ? ? ? ? ?f2 = sum; ? ? ? ?} ? ? ? ?return sum; ? ?}
我們也把這種自底向上的做法稱(chēng)之為遞推。
總結(jié)一下
當(dāng)你在使用遞歸解決問(wèn)題的時(shí)候,要考慮以下兩個(gè)問(wèn)題
(1). 是否有狀態(tài)重復(fù)計(jì)算的,可不可以使用備忘錄法來(lái)優(yōu)化。
(2). 是否可以采取遞推的方法來(lái)自底向上做,減少一味遞歸的開(kāi)銷(xiāo)。
今天就先講到這里,之后有時(shí)間再來(lái)多謝一些其他的。如果覺(jué)得不錯(cuò),不妨點(diǎn)個(gè)贊。
-
算法
+關(guān)注
關(guān)注
23文章
4628瀏覽量
93186 -
代碼
+關(guān)注
關(guān)注
30文章
4821瀏覽量
68890
原文標(biāo)題:一些常用的算法技巧總結(jié)
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
干貨總結(jié):室內(nèi)定位技術(shù)的3大常用算法
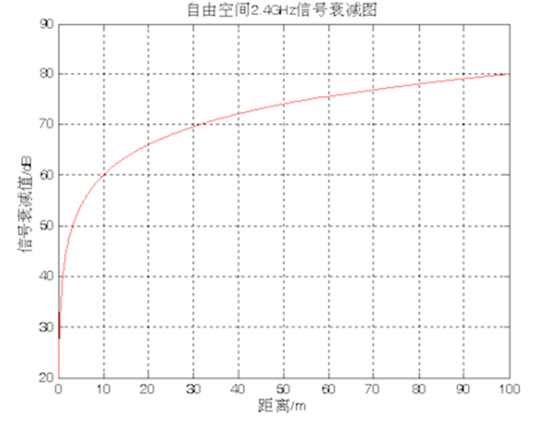
數(shù)字圖像基本處理算法小結(jié)
吳鑒鷹總結(jié)的單片機(jī)常用算法
單片機(jī)C語(yǔ)言常用算法PDF下載
嵌入式單片機(jī)程序架構(gòu)之時(shí)間片輪詢(xún)法
路由器常用基礎(chǔ)知識(shí)總結(jié)
MATLAB常用函數(shù)總結(jié)(表格)
Adaboost算法總結(jié)
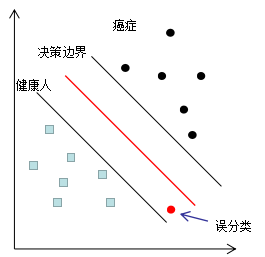
機(jī)器學(xué)習(xí)算法常用指標(biāo)匯總

vc++-CDC常用函數(shù)總結(jié)

圖像處理常用算法總結(jié)




 常用的算法技巧總結(jié)
常用的算法技巧總結(jié)











評(píng)論