編者按：DM Labs創始人、DIGINETICA首席數據官Alexey Natekin講解了梯度提升算法的原理。

大家好！目前為止，我們已經介紹了從探索性分析到時序分析在內的9個主題。今天我們將介紹最流行、最實用的機器學習算法之一：梯度提升。

概覽

導言和梯度提升的歷史

GBM算法

損失函數

相關資源

導言和梯度提升的歷史

在機器學習領域，梯度提升屬于人盡皆知的技術。許多數據科學家的工具箱中收錄了這一技術，因為它在任何給定的（未知）問題上都能得到很好的結果。

此外，XGBoost是ML競賽冠軍的常用配方。它是如此流行，以至于堆疊XGBoost的想法都成了meme。而且，梯度提升也是許多推薦系統的重要組成部分；有時它甚至成為了品牌。讓我們看下梯度提升的歷史和發展。

梯度提升源于這樣一個問題：能從大量相對弱小、簡單的模型得到一個強力模型嗎？這里“弱小模型”指的不是決策樹這樣簡單基本的模型，而是精確度表現糟糕的模型，糟糕到比隨機猜測好一點的程度。

研究發現，在數學上而言，這一問題的答案是肯定的，但開發實際可用的算法（例如，AdaBoost）花了好幾年。這些算法采用了貪婪的做法：首先，通過重新加權輸入數據創建簡單模型（基本算法）的線性組合；接著，基于之前錯誤預測的對象（給予更大權重）創建模型（通常是決策樹）。

很多機器學習課程討論了AdaBoost——GBM的祖先。然而，現在看來，AdaBoost不過是GBM的一個特定變體。

這一算法本身定義權重的直覺很清晰，通過可視化的方法很好解讀。讓我們查看下面的玩具分類問題，我們將在AdaBoost的每次迭代中在深度為1的樹間分割數據。

數據點的大小對應其權重，為不正確的預測分配。在每次迭代中，我們看到因為未能正確分類權重增加了。然而，如果我們進行加權投票，就能得到正確的分類：

下面是一個更詳細的AdaBoost的例子，我們看到，隨著迭代的進行，權重增加了，特別是在分類的邊界處。

AdaBoost效果不錯，但為何這一算法如此成功卻缺乏解釋，這正是一些疑惑產生的源頭。有些人認為AdaBoost是一個超級算法，一枚銀彈，但另一些人顧慮重重，相信AdaBoost只不過是過擬合。

過擬合問題確實存在，特別是當數據具有強離群值時。因此，AdaBoost在這類問題上的表現不穩定。幸運的是，一些斯坦福統計學教授開始研究這一算法（這些教授發明了Lasso、Elastic Net、隨機森林）。1999年，Jerome Friedman推廣了提升算法——梯度提升（機器），簡稱GBM。Friedman的這項工作為采用提升優化這個一般方法的許多算法提供了統計學基礎。

CART，bootstrap在內的許多算法源自斯坦福統計學部門。這些算法的提出，為他們在未來的教科書中留下了位置。這些算法非常實用，而一些最近的工作尚未廣泛普及。例如，glinternet。

網上沒有太多Friedman的視頻，不過，有一個非常有趣的訪談，關于如何提出CART，以及CART如何解決統計學問題（很像今天的數據分析和數據科學）：https://youtu.be/8hupHmBVvb0 另外推薦Hastie的講座：https://youtu.be/zBk3PK3g-Fc，我們今天日常使用的很多方法的創造者對數據分析的回顧。

GBM的歷史

GBM從提出到成為數據科學工具箱的必備組件花了十多年。GBM的擴展用于不同統計學問題：GBM模型加強版GLMboost、GAMboost，用于存活曲線的CoxBoost，用于排序的RankBoost和LambdaMART。

GBM的許多實現以不同的名字出現在不同的平臺上：隨機GBM，GBDT（梯度提升決策樹），GBRT（梯度提升回歸樹），MART（多重累加回歸樹）…… 此外，由于ML社區各自為營，很難追蹤梯度提升變得多么普及。

同時，梯度提升大量用于搜索排序。搜索排序問題可以基于懲罰輸出順序誤差的損失函數重新表述，從而便于直接插入GBM。AltaVista是第一個在搜索排序中引入梯度提升的公司之一。很快，Yahoo、Yandex、Bing等也采用了這一想法。自此之后，梯度提升不再僅僅用于研究之中，同時成為業界的核心技術之一。

ML競賽，特別是Kaggle，在梯度提升的流行中起到了主要作用。Kaggle為研究人員提供了一個可以和世紀各地大量參與者一起競爭數學科學問題的公共平臺。在Kaggle上，可以在真實數據上測試新算法，這就給了算法“閃耀”的機會。Kaggle提供了模型在不同競賽數據集上的表現的完整信息。這正是梯度提升用于Kaggle競賽后所發生的事（自2011年以來，Kaggle冠軍的訪談中大多提到自己使用了梯度提升）。XGBoost庫出現后迅速流行開來。XGBoost并不是一個新穎獨特的算法；它只是經典GBM的一個極其高效的實現（加上了一些啟發式算法）。

GBM的經歷也是今天許多ML算法的經歷：初次出現之后，從數學問題和算法工藝到成功的實踐應用和大規模使用花了許多年。

GBM算法

我們將求解一個一般的監督學習設定下的函數逼近問題。特征集記為X，目標變量記為y，我們需要重建y = f(x)這一依賴。我們通過逼近f(x)重建這一依賴，基于損失函數L(y, f)判斷哪個逼近較好：

在此階段，我們對f(x)的種類、逼近模型、目標變量的分布不做任何假定。我們只期望L(y, f)是可微的。最小化數據損失（基于具體數據集的總體均值）的表達式為：

不幸的是，這樣的函數不僅數目很多，而且函數空間有著無窮維。因此，需要限制搜索空間至某些函數家族。這大大簡化了目標，因為我們現在只需解決參數值的優化問題。

查找最佳參數經常不存在簡單的解析解，我們通常迭代地逼近參數。我們在一開始寫下經驗損失函數，讓我們可以基于數據演算參數，并寫下M次迭代后的參數逼近之和：

接著，我們只需找到一個合適的最小化上式的迭代算法。梯度下降是最簡單、最常用的選項。我們定義損失函數在當前逼近上的梯度，然后在迭代演算中減去梯度。最終我們只需初始化第一次逼近，并選擇迭代次數M。

函數梯度下降

讓我們想象一下，我們可以在函數空間中進行優化，迭代搜索函數逼近本身。我們將逼近表述為增量改進之和，每個改進都是一個函數。

目前為止沒有實際發生什么事；我們只是決定并不以具有大量參數的巨大模型（例如，神經網絡）的方式搜索逼近，而是以函數之和的方式搜索逼近，假想我們在函數空間中移動。

為了完成這一任務，我們需要限制搜索空間至某個函數家族：

在迭代的每一步，我們需要選擇最優參數ρ ∈ ?。第t步需要求解的問題如下：

這是關鍵之處。我們以一般形式定義了所有的目標，假裝我們可以為任意種類的損失函數L(y, f(x, θ))定義任意種類的模型h(x, θ)。在實踐中，這極為困難。幸運的是，有一種簡單方法可以解決這一任務。

一旦我們知道了損失函數的梯度表達式，我們就可以在數據上計算相應的值。這樣，我們可以訓練模型，使其預測和梯度（取反）更相關。換句話說，我們將基于預測和這些殘差的最小平方差糾正預測。因此，第t步最終轉化為以下問題：

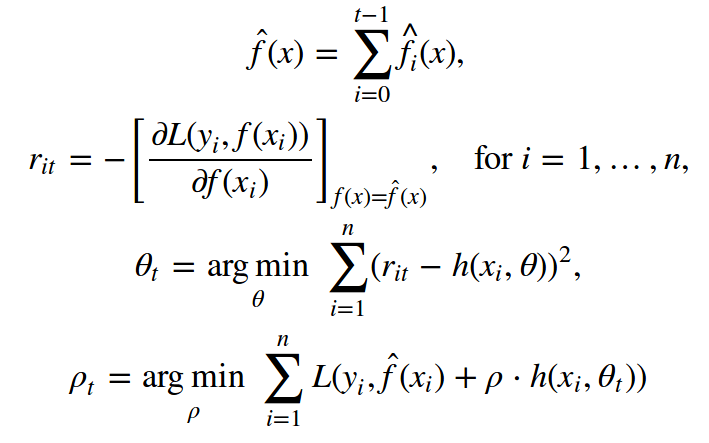
Friedman的經典GBM算法

下面我們講下Jerome Friedman在1999年提出的經典GBM算法。它是一個具備以下要素的監督算法：

數據集{(xi, yi)}i=1,…,n

迭代數M

梯度定義良好的損失函數L(y, f)

基礎算法對應的函數家族h(x, θ)及其訓練過程

h(x, θ)的其他超參數（例如，決策樹的深度）

還剩下初次逼近f0(x)沒講。出于簡單性，初次逼近使用一個常數γ。這個常數值γ和最優參數ρ，均通過二元搜索或其他基于初始損失函數（非梯度）的線搜索算法得出。

GBM算法過程如下：

使用常數值初始化GBM：

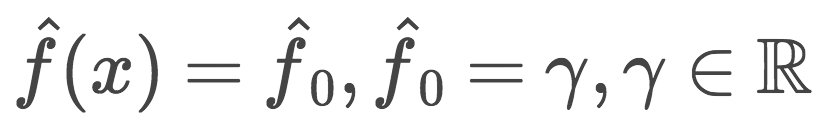
每次迭代t = 1, …, M，重復以上逼近過程；

在i = 1, …, n上計算偽殘差rt：

以偽殘差{(xi, rit)}i=1,…,n上的回歸作為基礎算法ht(x)

據ht(x)的初始損失函數找出最優參數ρt：

保存

更新當前逼近：

組成最終GBM模型：

征服Kaggle和全世界

GBM如何工作

讓我們通過一個例子演示下GBM是如何工作的。在這個玩具示例中，我們需要重建以下函數：

這是一個實數值的回歸問題，所以我們將選擇均方誤差損失函數。我們將生成300對觀測，然后通過深度為2的決策樹逼近它們。羅列下使用GBM所需的要素：

玩具數據 {(xi, yi)}i=1,…,300?

迭代數 M = 3 ?

均方誤差損失函數 L(y,f) = (y-f)2?

L(y,f)（L2損失）的梯度不過是殘差r = (y-f) ?

基礎算法h(x)為決策樹 ?

決策樹的超參數：樹深等于2 ?

就均方誤差而言，γ和ρt的初始化很簡單。我們初始化GBM時將所有參數ρt設為1，γ據下式確定：

我們運行GBM然后繪制兩種圖形：當前逼近（藍色）和在偽殘差上構建的每棵樹（綠色）。

從上圖我們可以看到，我們的決策樹在第二次迭代時恢復了函數的基本形式。然而，第一次迭代時算法只創建了函數的“最左部分”（x ∈ [-5, -4]）。這是因為我們的決策樹不具備足夠的深度一下子創建對稱分支，所以它首先關注誤差較大的最左部分。

剩下的過程不出我們的意料——每一步的偽殘差下降了，隨著迭代的進行，GBM越來越好地逼近原函數。然而，決策樹的構造決定了它無法逼近一個連續函數，這意味著在這個例子中GBM的效果不是很理想。如果你想以可視化的方式試驗GBM函數逼近，可以使用Brilliantly wrong提供的工具：http://arogozhnikov.github.io/2016/06/24/gradient_boosting_explained.html

損失函數

如果我們想要求解一個分類問題，而不是回歸問題，那需要做什么變動？只需選擇一個合適的損失函數L(y,f)。正是這一最重要的高層的契機，決定了我們將如何優化，以及我們期望最終的模型將具有哪些特性。

我們并不需要自行發明這些——研究人員已經替我們做了。現在我們將探索用于最常見的兩種目標的損失函數：回歸和二元分類。

回歸損失函數

最常用的選項為：

L(y,f) = (y-f)2，即L2損失或高斯損失。這一經典的條件平均數是最簡單也是最常見的情形。如果我們不具備額外信息，也不要求模型的魯棒性，那么可以使用高斯損失。

L(y,f) = |y-f|，即L1損失或拉普拉斯損失。事實上它定義了條件中位數。如我們所知，中位數對離群值的魯棒性更好，所以這一損失函數在某些情形下表現更好。對大偏差的懲罰不像L2那么大。

Lq損失或分位數損失：

其中α ∈ (0,1). Lq使用分位數而不是中位數，例如，α = 0.75. 如下圖所示，這一函數是不對稱的，對定義的分位數右側的觀測懲罰力度更大。

讓我們試驗下Lq的效果。目標是恢復余弦的條件75%分位數。列出GBM所需要素：

玩具數據 {(xi, yi)}i=1,…,300 ?

迭代數 M = 3 ?

損失函數 L0.75(y,f) ?

L0.75(y,f)的梯度 ?

基礎算法h(x)為決策樹 ?

決策樹的超參數：樹深等于2 ?

初次逼近將使用所需的y的分位，但我們并不知道最佳參數該取什么值，所以我們將使用標準的線搜索。

結果等價于L2損失加上約0.135的偏置。但是如果我們使用的是90%分位數的話，那我們就不會有足夠的數據了（失衡分類）。當我們處理非標準問題時，需要記住這一點。

人們為回歸任務開發了許多損失函數。例如，Huber損失函數，離群值較少時，和L2類似，但超出定義的閾值后，轉變為L1，從而降低離群值的影響。

下面是一個例子，數據生成自函數y = sin(x) / x，加上噪聲（正態分布和伯努利分布的混合分布）。

在這個例子中，我們使用樣條作為基礎算法。你看，梯度提升并不總是需要使用決策樹的。

上圖很清楚地顯示了L2、L1、Huber損失的區別。如果我們為Huber損失選擇最優的參數，可以得到最佳的逼近。

不幸的是，流行的庫/軟件包中，只有很少支持Huber損失；h2o支持，XGBoost不支持。Huber損失和條件expectiles有關——相對而言更奇異，但仍然值得了解的知識。

分類損失函數

現在讓我們看下二元分類問題。技術上說，我們有可能基于L2回歸解決這一問題，但這不是正規做法。

目標變量的分布（y ∈ {?1,1}）需要我們使用對數似然，所以我們需要不同的損失函數。最常見的選擇為：

L(y,f) = log(1 + exp(?2yf))，即邏輯損失或伯努利損失。這個損失函數有一個有趣的性質，它甚至會懲罰正確預測的分類——不僅優化損失，同時使分類分得更開。

L(y,f) = exp(-yf)，即AdaBoost損失。使用該損失函數的AdaBoost等價于GBM。從概念上講，這個函數和邏輯損失很相似，但對錯誤預測有更重的指數懲罰。

讓我們生成新的分類問題的玩具數據。我們將使用前面提到的加噪余弦作為基礎，并使用符號函數得到目標變量的分類。我們的玩具數據如下圖所示（加入了抖動噪聲）：

我們將使用邏輯損失。讓我們再一次羅列GBM的要素：

玩具數據 {(xi, yi)}i=1,…,300, y ∈ {?1,1} ?

迭代數 M = 3 ?

損失函數為邏輯損失，梯度計算方法見下 ?

基礎算法h(x)為決策樹 ?

決策樹的超參數：樹深等于2 ?

邏輯損失梯度計算

這次，算法的初始化要困難一點。首先，我們的分類并不均衡（63%對37%）。其次，損失函數的初始化沒有已知的解析公式，所以我們需要通過搜索解決：

我們的最優初始逼近在-0.273左右。你可能猜想過它應該是負值，因為預測所有項為最流行的分類是最有利的，但沒有求出精確值的公式。現在我們終于可以開始GBM過程了：

算法成功恢復了分類的分隔。你可以看到“低部”是如何分開的，因為決策樹對負分類（-1）的正確預測更有信心，也可以看到模型如何擬合混合分類。很明顯，我們得到了大量正確分類的觀測，一些誤差較大的觀測則是數據中的噪聲所致。

權重

有時候，我們會碰到想要使用更特定的損失函數的情形。例如，在財經時序數據上，我們可能需要給時序中的大變動更大的權重；在離網率預測問題中，預測高LTV（客戶未來會帶來多少利潤）的客戶的離網率更有用。

統計學戰士可能想要自己發明損失函數，寫下它的梯度（包括海森矩陣），并仔細檢查這一函數是否滿足需要具備的性質。然而，有很大的幾率會在某處犯下錯誤，導致計算困難，花費過量時間排錯。

有鑒于此，人們提出了一種非常簡單的做法（實踐中很少有人記得）：使用權重分配函數加權觀測。最簡單的一個例子是為了平衡分類加上的權重。一般來說，如果我們知道數據的某個子集（輸入變量和目標變量）對我們的模型更重要，那么我們可以直接給它們分配較大的權重w(x, y)。

權重需滿足以下條件：

權重能夠顯著降低花在為當前任務調整損失函數上的時間，并鼓勵你試驗目標模型的性質。權重分配可以充分發揮你的創造性。比如，簡單地加上標量權重：

對任意權重而言，我們未必知道模型的統計學性質。將權重與y值相聯系經常會變得太復雜。例如，使用正比于|y|的權重在L1損失和L2損失中是不等價的（梯度不考慮預測值本身）。

現在，為我們的玩具數據創建一些非常奇異的權重。我們將定義一個強力的非對稱加權函數：

基于這樣的權重，我們期望得到兩個屬性：X的負值細節更少，形成類似初始余弦的函數。我們采用了上一個例子中的GBM，加以調整，最終得到：

我們取得了意料之中的結果。首先，我們可以看到，第一次迭代上的偽殘差有著很大的差距，看起來幾乎是原本的余弦函數。其次，函數左半部分的圖形常常被忽略，函數更偏向具有更大權重的有半部分。第三，第3次迭代得到的函數看起來和原本的余弦函數類似（同時開始稍微有點過擬合了）。

權重是一個高風險的強力工具，可用于控制模型的性質。如果你打算優化損失函數，值得首先嘗試下給觀測加上權重這一更簡單的問題。

結語

今天，我們學習了梯度提升背后的理論。GBM不是一個特定的算法，而是創建模型集成的一種常見方法。這一方法具有足夠的靈活性和擴展性——可以訓練大量模型，使用不同的損失函數和加權函數。

實際項目和ML競賽表明，在標準問題上（圖像、音頻、非常稀疏的數據除外），GBM經常是最有效的算法（更別說在堆疊和高層集成中，GBM幾乎總是其中的一部分）。同時，強化學習中GBM也用得不少（Minecraft, ICML 2016）。順便提下，計算機視覺領域，現在還使用基于AdaBoost的維奧拉-瓊斯算法。

在這篇文章中，我們有意省略了關于GBM的正則化、隨機性、超參數的問題。我們一直使用很小的迭代數M = 3并非出于偶然。如果我們使用30棵樹訓練GBM的話，結果的預測性不會那么好：

良好的擬合

過擬合

圖片來源： arogozhnikov.github.io