在前幾次筆記中，筆者基本上將卷積神經網絡的基本原理給講完了。從本次筆記開始，筆者在深度學習筆記中會不定期的對 CNN 發展過程中的經典論文進行研讀并推送研讀筆記。今天筆者就和大家一起學習卷積神經網絡和深度學習發展歷史上具有奠基性的經典論文之一的關于 LeNet-5 網絡一文。LeNet-5 是由具有卷積神經網絡之父之美譽的 Yann LeCun 在1998年發表在 IEEE 上面的一篇 Gradient-based learning applied to document recognition 上提出來的，所以直接由 LeCun 大佬名字命名了。
論文原文：
http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf

LeNet-5 網絡結構

該篇論文有 42 頁，但關于 LeNet-5 網絡的核心部分并沒有那么多，我們直接定位第二章的B 小節進行閱讀。LeNet-5 的網絡結構如下：

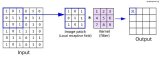
LeNet-5 共有 7 層，輸入層不計入層數，每層都有一定的訓練參數，其中三個卷積層的訓練參數較多，每層都有多個濾波器，也叫特征圖，每個濾波器都對上一層的輸出提取不同的像素特征。所以 LeNet-5 的簡略結構如下：

輸入-卷積-池化-卷積-池化-卷積（全連接）-全連接-全連接（輸出）

各層的結構和參數如下：
C1層是個卷積層，其輸入輸出結構如下：
輸入： 32 x 32 x 1 濾波器大小： 5 x 5 x 1 濾波器個數：6
輸出： 28 x 28 x 6
參數個數： 5 x 5 x 1 x 6 + 6 = 156

P2層是個池化層，其輸入輸出結構如下：
輸入： 28 x 28 x 6 濾波器大小： 2 x 2 濾波器個數：6
輸出： 14 x 14 x 6
參數個數：2 x 6 = 12
在原文中，P1池化層采用的是平均池化，鑒于現在普遍都使用最大池化，所以在后面的代碼實現中我們統一采用最大池化。

C3層是個卷積層，其輸入輸出結構如下：
輸入： 14 x 14 x 6 濾波器大小： 5 x 5 x 6 濾波器個數：16
輸出： 10 x 10 x 16
參數個數： 5 x 5 x 6 x 16 + 16 = 2416

P2 池化之后的特征圖組合計算得到C3的濾波器個數。

P4層是個池化層，其輸入輸出結構如下：
輸入： 10 x 10 x 16 濾波器大小： 2 x 2 濾波器個數：16
輸出： 5 x 5 x 16
參數個數： 2 x 16 = 32

C5層在論文中是個卷積層，但濾波器大小為 5 x 5，所以其本質上也是個全連接層。如果將5 x 5 x 16 拉成一個向量，它就是一個全連接層。其輸入輸出結構如下：
輸入： 5 x 5 x 16 濾波器大小： 5 x 5 x 16 濾波器個數：120
輸出： 1 x 1 x 120
參數個數： 5 x 5 x 16 x 120 + 120 = 48120

F6層是個全連接層，全連接的激活函數采用的是 tanh 函數，其輸入輸出結構如下：
輸入：120
輸出：84
參數個數：120 x 84 + 84 = 10164

F7層即輸出層，也是個全連接層，其輸入輸出結構如下：
輸入：84
輸出：10
參數個數： 84 x 10 + 10 = 850

LeNet-5 的 Tensorflow 實現

我們前面關于如何使用 Tensorflow 搭建卷積神經網絡的過程可以定下實現 LeNet-5 的基本思路。如果在 python 中寫的時候我們需要定義創建輸入輸出的占位符變量模塊、初始化各層參數模塊、創建前向傳播模塊、定義模型優化迭代模型，以及在最后設置輸入數據。

下面筆者用以上思路編寫一個 LeNet-5 的簡單實現代碼。
導入相關庫和創建輸入輸出的占位符變量：

importtensorflowastf
importnumpyasnp
fromtensorflow.examples.tutorials.mnistimportinput_data
defcreate_placeholder():
X=tf.placeholder(tf.float32,shape=(None,28*28))
Y=tf.placeholder(tf.float32,shape=(None,10))
keep_prob=tf.placeholder(tf.float32)
returnX,Y,keep_prob

初始化各層參數：

definitialize_parameters():
W1=tf.get_variable('W1',[5,5,1,6],initializer=tf.contrib.layers.xavier_initializer())
b1=tf.get_variable('b1',[6],initializer=tf.zeros_initializer())

W2=tf.get_variable('W2',[5,5,6,16],initializer=tf.contrib.layers.xavier_initializer())
b2=tf.get_variable('b2',[16],initializer=tf.zeros_initializer())

W3=tf.get_variable('W3',[5,5,16,120],initializer=tf.contrib.layers.xavier_initializer())
b3=tf.get_variable('b3',[120],initializer=tf.zeros_initializer())

W4=tf.get_variable('W4',[120,84],initializer=tf.contrib.layers.xavier_initializer())
b4=tf.get_variable('b4',[84],initializer=tf.zeros_initializer())

W5=tf.get_variable('W5',[84,10],initializer=tf.contrib.layers.xavier_initializer())
b5=tf.get_variable('b5',[10],initializer=tf.zeros_initializer())

para={'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2,
'W3':W3,
'b3':b3,
'W4':W4,
'b4':b4,
'W5':W5,
'b5':b5}
returnpara

創建 LeNet-5 的前向計算：

defforward_propagation(X,para,dropout):

X=tf.reshape(X,[-1,28,28,1])
X=tf.pad(X,[[0,0],[2,2],[2,2],[0,0]])

c1=tf.nn.conv2d(X,para['W1'],strides=[1,1,1,1],padding='VALID')+para['b1']
p2=tf.nn.max_pool(c1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='VALID')
c3=tf.nn.conv2d(p2,para['W2'],strides=[1,1,1,1],padding='VALID')+para['b2']
p4=tf.nn.max_pool(c3,ksize=[1,2,2,1],strides=[1,2,2,1],padding='VALID')
c5=tf.nn.conv2d(p4,para['W3'],strides=[1,1,1,1],padding='VALID')+para['b3']
c5=tf.contrib.layers.flatten(c5)
f6=tf.nn.tanh(tf.add(tf.matmul(c5,para['W4']),para['b4']))
f7=tf.nn.tanh(tf.add(tf.matmul(f6,para['W5']),para['b5']))
f7=tf.nn.dropout(f7,dropout)
returnf7

創建模型優化計算函數：

最后傳入 mnist 數據和相關超參數：

本文來自《自興人工智能》項目部：凱文