今天,來看一看連續時間信號的重建(或者稱為信號的恢復)。首先呢,來嘮一嘮,“重建”或者稱為“恢復”是何意?不知道大家如何想的,反正我在當學生學這部分內容時,我的感覺是,好不容易采樣了,為啥又去恢復?這不吃飽了撐的嗎?
其實呢,我們可以從兩方面來理解信號重建的意義:一方面,從理論分析的層面來說,我們可以通過信號的重建,來證明抽取后的離散樣值,確實能代表原來連續時間信號的全部信息。第二個,在實際應用的層面,如下圖所示,是一般的數字信號處理系統框圖,中間的“通用/專用計算機”來完成對數字信號的處理。它的前面(紅色框框),需要把模擬信號轉換成數字信號,它的后面(黃色框框),又需要把處理后的數字信號,轉換為模擬信號。可以說,我們信號與系統中所學的“時域抽樣”,對應AD轉換的理想模型;而“信號的重建(恢復)”對應DA轉換的理想模型。
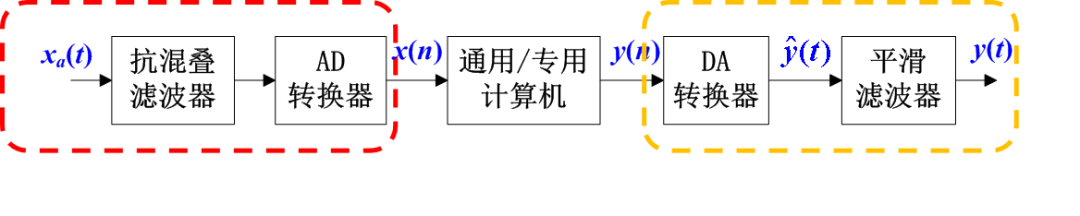
圖0
本文不涉及實際數字信號處理中的ADC和DAC,關于這部分內容,感興趣的同學可以參考本公眾號以前發過的文章,鏈接如下:
數字信號處理中的采樣與信號重建
本文主要討論三種時域采樣模型對應的連續時間信號的重建問題。
總體思路:如前文所述,不管哪種模型,采樣后信號的頻譜,都是原來連續時間信號頻譜的周期延拓,在滿足采樣定理要求的前提下,頻域的周期延拓就不會混疊,這樣,只要通過合適的低通濾波器,把周期延拓后其他的頻譜都濾除,只保留w=0附近的這部分頻譜,并且要使得這部分頻譜與原來的連續時間信號的頻譜完全相同,就可以恢復原始的連續時間信號了。
第一種,理想沖激串采樣
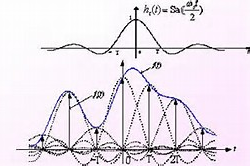
連續時間信號的頻譜和經過理想沖激串采樣后信號的頻譜如下圖所示。因此,只要把抽樣信號通過理想低通濾波器,理想低通濾波器通帶的增益為常數T(正好抵消抽樣信號頻譜周期延拓時的系數1/T),并且理想低通濾波器的截止頻率wc正好位于wm和ws-wm之間,也就是使得w=0附近的這部分頻譜完全通過,而其他的頻譜完全濾除掉,就可以了。
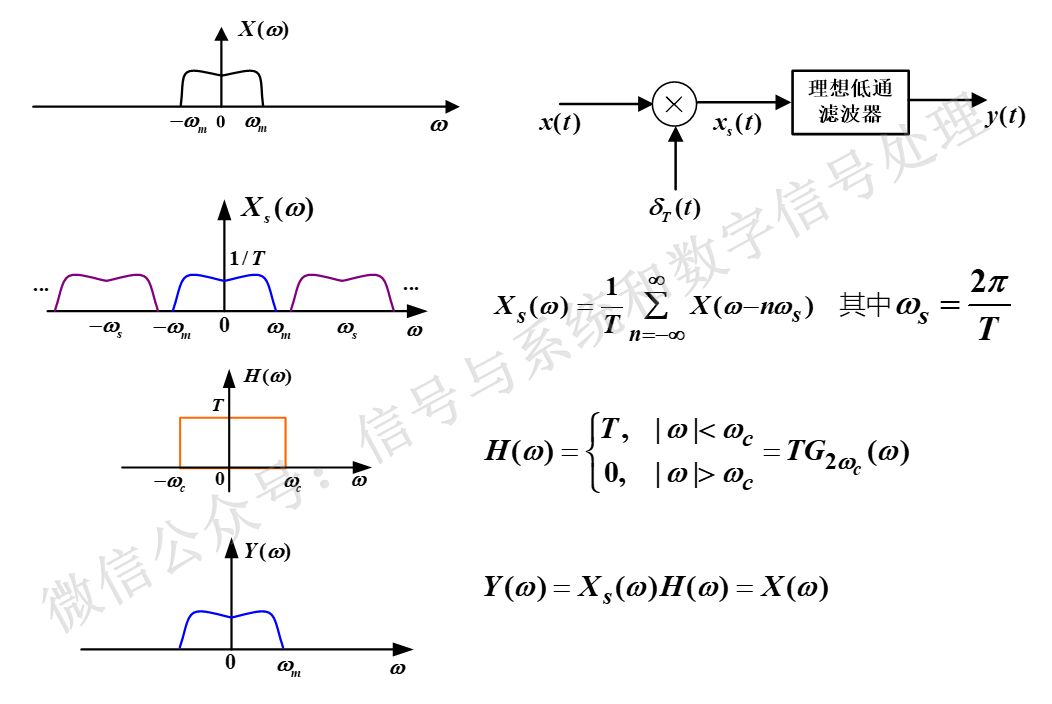
圖1
第二種,脈沖串采樣(曲頂采樣)
如圖2所示,看抽樣信號的頻譜Xs(jw)這個公式,看似復雜,其實不然你,把這個求和形式展開寫,發現每個周期延拓的頻譜前面乘的這個系數,看上去像個sinc函數,但實際上,僅僅是sinc函數在延拓的這個位置處的取值(是個常數)而已。w=0位置處的這個系數,是τ/T,所以理想低通濾波器的通帶增益,只要把這個系數τ/T抵消掉,也就是T/τ,就可以了。這樣就很容易得到用于信號重建的理想低通濾波器的頻率響應H(jw)的表達式。與圖1相比,僅僅是T變成了T/τ而已。
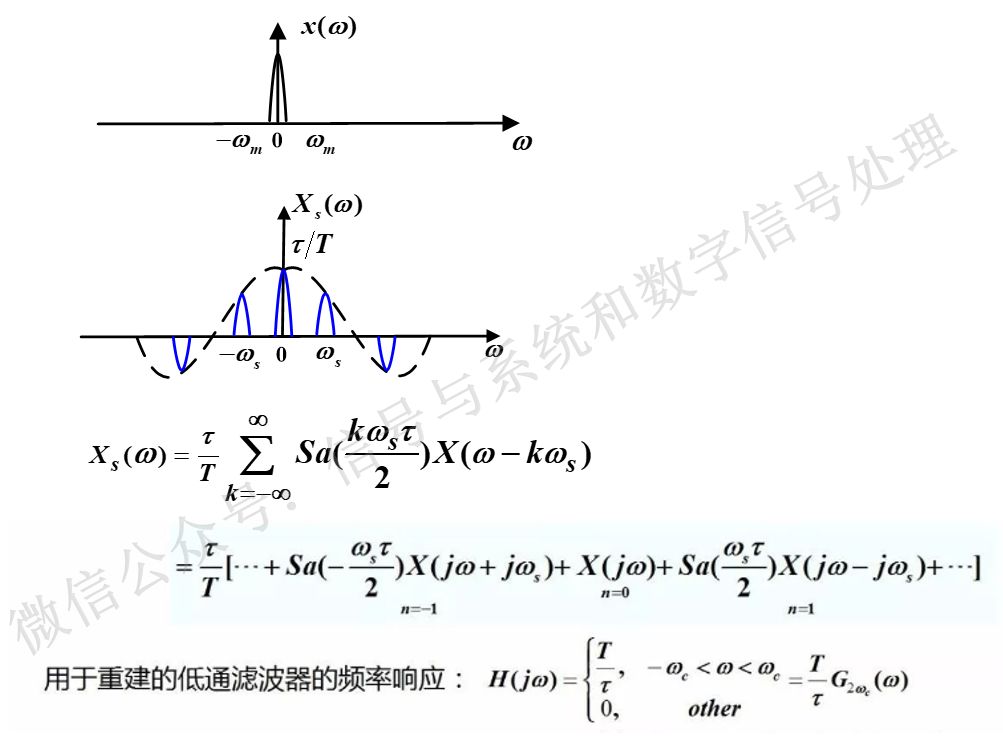
圖2
第三種,脈沖串采樣(平頂采樣)
平頂抽樣的情況稍顯復雜,用于重建的濾波器,依然是低通濾波器,但它的頻率響應函數,就不能再是一個常數,而是要把周期延拓時所乘的sinc函數抵消掉,所以,重建的低通濾波器的通帶增益是把sinc函數放在分母上,如圖3中的公式所示。
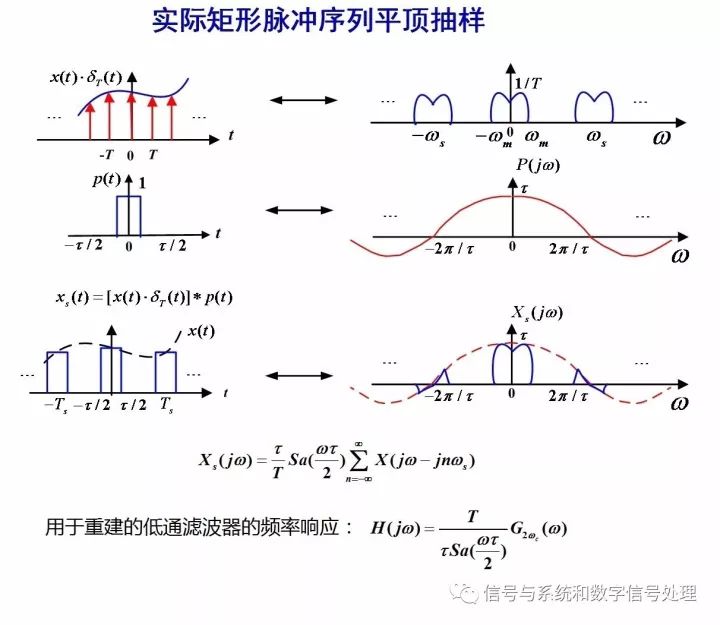
-
信號處理
+關注
關注
48文章
1032瀏覽量
103315 -
模擬信號
+關注
關注
8文章
1134瀏覽量
52499 -
DA轉換
+關注
關注
1文章
30瀏覽量
17728
原文標題:經常出現在考題中的三種時域采樣模型(第二部分)——信號的重建
文章出處:【微信號:SignalAndSystem_DSP,微信公眾號:信號與系統和數字信號處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
信號與系統教程之連續時間系統的時域分析
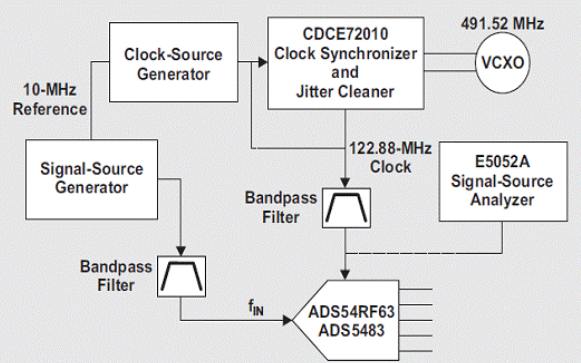
連續時間系統時域分析的MATLAB實現
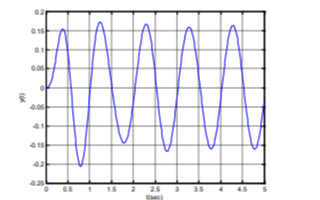




 連續時間信號的重建分析概述
連續時間信號的重建分析概述












評論