編者按：訓練集/測試集劃分和交叉驗證一直是數據科學和數據分析中的兩個相當重要的概念，它們也是防止模型過擬合的常用工具。為了更好地掌握它們，在這篇文章中，我們會以統計模型為例，先從理論角度簡要介紹相關術語，然后給出一個Python實現的案例。

什么是模型過擬合/欠擬合

在統計學和機器學習中，通常我們會把數據分成兩個子集：訓練數據和測試數據（有時也分為訓練、驗證、測試三個），然后用訓練集訓練模型，用測試集檢驗模型的學習效果。但當我們這么做時，模型可能會出現以下兩種情況：一是模型過度擬合數據，二是模型不能很好地擬合數據。常言道過猶不及，這兩種情況都是我們要極力規避的，因為它們會影響模型的預測性能——預測準確率較低，或是泛化性太差，沒法把學到的經驗推廣到其他數據上（也就是沒法預測其他數據）。

過擬合

模型過擬合意味著我們把模型“訓練得太好了”，通過一遍又一遍的訓練，它已經把訓練數據的特征都“死記硬背”了下來。這在模型過于復雜（和觀察樣本數相比，模型設置的特征/變量太多）時往往更容易發生。過擬合的缺點是模型只對訓練數據非常準確，但在未經訓練的數據或全新數據上非常不準確，因為它不是泛化的，沒法推廣結果，對其他數據作出任何推斷。

更確切地說，過擬合的模型學習到的只是訓練數據中的“噪聲”，而不是數據中變量之間的實際關系。顯然，這些“噪聲”是訓練數據獨有的，這也決定了它不能準確預測任何新數據集。

欠擬合

和過擬合相比，欠擬合是另一個極端，它意味著模型連擬合訓練數據都做不到，沒能真正把握數據的趨勢。毫無疑問，一個欠擬合的模型也是不能被推廣到新數據的，它和過擬合恰恰相反，是模型過于簡單（沒有足夠的預測變量/自變量）的結果。例如，當我們用線性模型（比如線性回歸）擬合非線性數據時，模型就很可能會欠擬合。

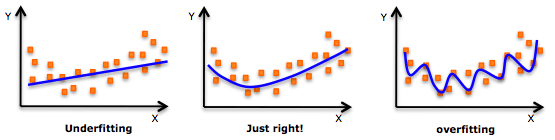
欠擬合、恰到好處和過擬合

值得注意的是，在實踐中，欠擬合遠不像過擬合那么普遍。但我們還是要做到在數據分析中同時警惕這兩個問題，找到它們的中間地帶。而解決問題的首選方案就是劃分訓練/測試數據和交叉驗證。

劃分訓練/測試數據

正如之前提到的，我們使用的數據通常會被劃分為訓練集和測試集。其中訓練集包含輸入的對應已知輸出，通過在上面進行訓練，模型可以把學到的特征關系推廣到其他數據上，而測試集就是模型性能的試金石。

那么在Python中，我們能怎么執行這個操作呢？這里我們介紹一種用Scikit-Learn庫，特別是traintestsplit的方法。讓我們先從導入庫開始：

import pandas as pd

from sklearn import datasets, linear_model

from sklearn.model_selection import train_test_split

from matplotlib import pyplot as plt

在上述代碼中：

第一行作用是把數據導入到pandas數據框架中，然后再進行分析；

第二行表示既然已經導入了數據集模塊，所以我們可以加載一個樣本數據集和linear_model來做線性回歸；

第三行表示已經導入了traintestsplit，所以可以把數據集分成訓練集和測試集；

第四行意味著導入pyplot以繪制數據圖。

下面我們以糖尿病數據集為例，從實踐中看看怎么把它導入數據框架，并定義各列的名稱。

數據集地址：scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html

# Load the Diabetes Housing dataset

columns =“age sex bmi map tc ldl hdl tch ltg glu”.split()# Declare the columns names

diabetes = datasets.load_diabetes()# Call the diabetes dataset from sklearn

df = pd.DataFrame(diabetes.data, columns=columns)# load the dataset as a pandas data frame

y = diabetes.target # define the target variable (dependent variable) as y

現在我們可以用traintestsplit函數劃分數據集。test_size = 0.2表示測試數據在數據集中的占比，一般情況下，訓練集和測試集的比例應該是80/20或70/30。

# create training and testing vars

X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.2)

print X_train.shape, y_train.shape

print X_test.shape, y_test.shape

(353,10)(353,)

(89,10)(89,)

將模型擬合到訓練數據上：

# fit a model

lm = linear_model.LinearRegression()

model = lm.fit(X_train, y_train)

predictions = lm.predict(X_test)

把模型放到測試數據上：

predictions[0:5]

array([205.68012533, 64.58785513,175.12880278,169.95993301,

128.92035866])

注：預測后面那個[0:5]表示只顯示前五個預測值，如果把它刪掉，模型會輸出所有預測值。

然后是繪制模型結果：

## The line / model

plt.scatter(y_test, predictions)

plt.xlabel(“TrueValues”)

plt.ylabel(“Predictions”)

最后輸出模型準確度分數：

print“Score:”, model.score(X_test, y_test)

Score:0.485829586737

到這里，劃分訓練集/測試集就完成了，如果總結整個過程，它可以被概括為先加載數據，將其分成訓練集和測試集，用回歸模型擬合訓練數據，基于訓練數據進行預測并在測試集上預測測試數據的結果。一切都好像很完美吧？其實不然，劃分數據集也有很多講究——如果我們劃分時沒有做到嚴格意義上的隨機呢？如果數據集本身存在明顯偏差，其中大部分數據都來自某省、某個收入水平的員工、某個特定性別的員工或只有特定年齡的人，該怎么辦？

即便我們一再避免，模型最后還是會過擬合，而這就是交叉驗證可以發揮作用的地方。

交叉驗證

為了避免因數據集偏差、劃分數據集不當引起模型過擬合，我們可以使用交叉驗證，它和劃分訓練集/測試集非常相似，但適用于數量上更多的子集。它的工作原理是先把數據分成k個子集，并從中挑選k-1個子集，在每個自己上訓練模型，最后再用剩下的最后一個子集進行測試。

劃分訓練集/測試集和交叉驗證

交叉驗證的方法有很多，這里我們只討論其中兩個：第一個是k-折交叉驗證，第二個是Leave One Out交叉驗證（LOOCV）。

k-折交叉驗證

在k-折交叉驗證中，我們將數據分成k個不同的子集（分成k折），并在k-1個子集上分別訓練單獨模型，最后用第k個子集作為測試數據。

以下是k-折交叉驗證的Sklearn文檔中的一個簡單示例：

from sklearn.model_selection importKFold# import KFold

X = np.array([[1,2],[3,4],[1,2],[3,4]])# create an array

y = np.array([1,2,3,4])# Create another array

kf =KFold(n_splits=2)# Define the split - into 2 folds

kf.get_n_splits(X)# returns the number of splitting iterations in the cross-validator

print(kf)

KFold(n_splits=2, random_state=None, shuffle=False)

它的結果是：

for train_index, test_index in kf.split(X):

print(“TRAIN:”, train_index,“TEST:”, test_index)

X_train, X_test = X[train_index], X[test_index]

y_train, y_test = y[train_index], y[test_index]

('TRAIN:', array([2,3]),'TEST:', array([0,1]))

('TRAIN:', array([0,1]),'TEST:', array([2,3]))

如你所見，這個函數將原始數據拆分為不同的數據子集。

LOOCV

LOOCV（留一驗證）是本文要介紹的第二種交叉驗證方法，它的思路和k-折交叉驗證其實有相似之處，但不同的是，它只從原數據集中抽取一個樣本作為測試數據，剩余的全是訓練數據，整個過程一直持續到每個樣本都被當做一次測試數據，最后再用平均值構建最終的模型。可以想見，這種方法勢必會得到大量的訓練集（等于樣本數），所以它的計算量會很大，更適合被用于小型數據集。

讓讓我們看一下它在Sklearn里的例子：

from sklearn.model_selection importLeaveOneOut

X = np.array([[1,2],[3,4]])

y = np.array([1,2])

loo =LeaveOneOut()

loo.get_n_splits(X)

for train_index, test_index in loo.split(X):

print("TRAIN:", train_index,"TEST:", test_index)

X_train, X_test = X[train_index], X[test_index]

y_train, y_test = y[train_index], y[test_index]

print(X_train, X_test, y_train, y_test)

它的輸出是：

('TRAIN:', array([1]),'TEST:', array([0]))

(array([[3,4]]), array([[1,2]]), array([2]), array([1]))

('TRAIN:', array([0]),'TEST:', array([1]))

(array([[1,2]]), array([[3,4]]), array([1]), array([2]))

那么對于這兩種交叉驗證方法，我們在實踐中該怎么取舍呢？事實上，子集越小、子集數量越多，模型的準確率就越高，但相應的，它的計算量也越多，對內存的要求也越大。因此，如果是非常小的數據集，建議大家還是用LOOCV；如果數據集略大，可以采用k-折，比如k=3是一個比較常用的超參數，當然你也可以視情況選擇5、10等。

split函數劃分 VS 交叉驗證

之前我們演示了用函數劃分糖尿病數據集的結果，這里我們嘗試對它做交叉驗證，看看有什么不同。首先，我們可以用cross_val_predict函數返回測試子集中每個數據點的預測值。

# Necessary imports:

from sklearn.cross_validation import cross_val_score, cross_val_predict

from sklearn import metrics

既然我們已經把數據集分成了測試集和訓練集，這里我們再在原有基礎上進行交叉驗證，看看準確率得分變化：

# Perform 6-fold cross validation

scores = cross_val_score(model, df, y, cv=6)

print“Cross-validated scores:”, scores

Cross-validated scores:[0.4554861 0.461385720.400940840.552207360.439427750.56923406]

得分從0.485提高到了0.569，雖然看起來不是很顯著，但不要心急，我們來繪制交叉驗證后的圖像：

# Make cross validated predictions

predictions = cross_val_predict(model, df, y, cv=6)

plt.scatter(y, predictions)

很明顯，這幅圖里的數據點比之前的圖密集多了，因為我們取cv=6。

從本質上來看，回歸模型就是用模型擬合數據，這之中肯定存在誤差，而衡量這個誤差大小的標尺是擬合優度。在眾多標準中，R2是度量擬合優度的一個常用統計量，這里我們計算一下模型的R2得分：

accuracy = metrics.r2_score(y, predictions)

print“Cross-PredictedAccuracy:”, accuracy

Cross-PredictedAccuracy:0.490806583864

以上就是文本想要介紹的全部內容，希望你能從中找到對自己有所幫助的東西！