“深度學習”雖然深奧，本質卻很簡單。無論是圖像識別還是語義分析，機器的“學習”能力都來源于同一個算法 — 梯度下降法 (Gradient Descent)。要理解這個算法，你所需要的僅僅是高中數學。在讀完這篇文章后，你看待 AI 的眼光會被永遠改變。

Google 研發了十年自動駕駛后，終于在本月上線了自動駕駛出租車服務。感謝“深度學習”技術，人工智能近年來在自動駕駛、疾病診斷、機器翻譯等領域取得史無前例的突破，甚至還搞出了些讓人驚艷的“藝術創作”：

Prisma 把你的照片變成藝術作品

AI 生成的奧巴馬講話視頻，看得出誰是本尊嗎？

開源軟件 style2paints 能自動給漫畫人物上色

如果不了解其中的原理，你可能會覺得這是黑魔法。

但就像愛情，“深度學習”雖然深奧，本質卻很簡單。無論是圖像識別還是語義分析，機器的“學習”能力都來源于同一個算法 — 梯度下降法 (Gradient Descent)。要理解這個算法，你所需要的僅僅是高中數學。在讀完這篇文章后，你看待 AI 的眼光會被永遠改變。

一個例子

我們從一個具體的例子出發：如何訓練機器學會預測書價。在現實中，書的價格由很多因素決定。但為了讓問題簡單點，我們只考慮書的頁數這一個因素。

在機器學習領域，這樣的問題被稱為“監督學習 (Supervised Learning)”。意思是，如果我們想讓機器學會一件事（比如預測書的價格），那就給它看很多例子，讓它學會舉一反三（預測一本從未見過的書多少錢）。其實跟人類的學習方法差不多，對吧？

現在假設我們收集了 100 本書的價格，作為給機器學習的例子。大致情況如下：

頁數

書價

接下來我們要做兩件事：

告訴機器該學習什么；

等機器學習。

告訴機器該學什么

為了讓機器聽懂問題，我們不能說普通話，得用數學語言向它描述問題，這就是所謂的“建模”。為了讓接下來的分析更直觀，我們把收集回來的例子畫在數軸上：

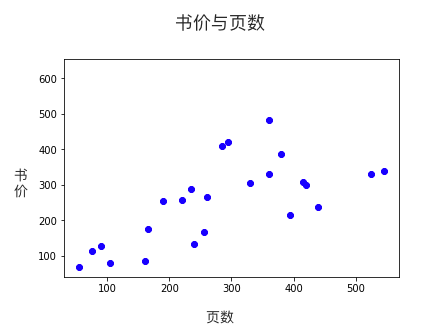
我們希望機器通過這些樣本，學會舉一反三，當看到一本從未見過的書時，也能預測價格。比如說，預測一本480頁的書多少錢：

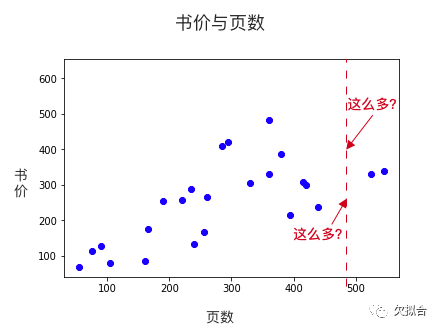
480頁的書多少錢？

觀察圖表，我們能看出頁數和書價大致上是線性關系，也就是說，我們可以畫一根貫穿樣本的直線，作為預測模型。

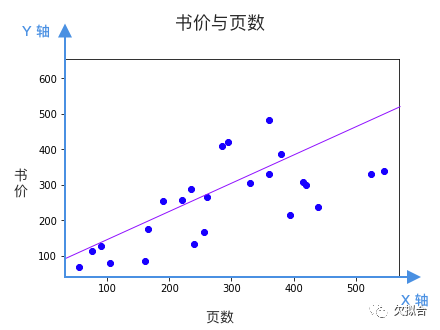
如果我們把頁數看作 X 軸，書價看作 Y 軸，這根直線就可以表示為：

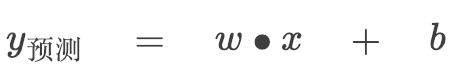
w 決定直線的傾斜程度，b 決定這根直線和 Y 軸相交的位置。問題是，看起來有很多條線都是不錯的選擇，該選哪條？換句話說 w 和 b 該等于多少呢？

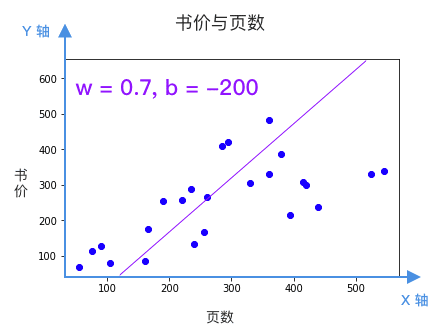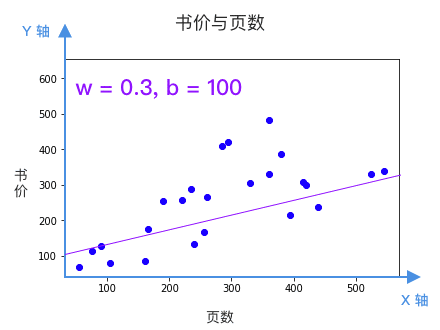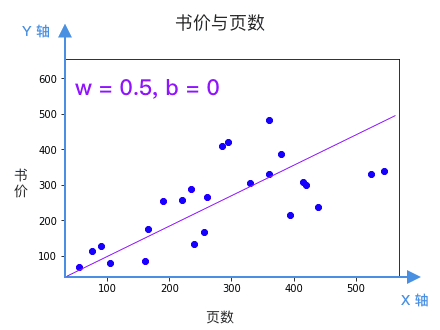
每根直線都是一個候選的模型，該選哪個？

顯然，我們希望找到一根直線，它所預測的書價，跟已知樣本的誤差最小。換句話說，我們希望下圖中的所有紅線，平均來說越短越好。

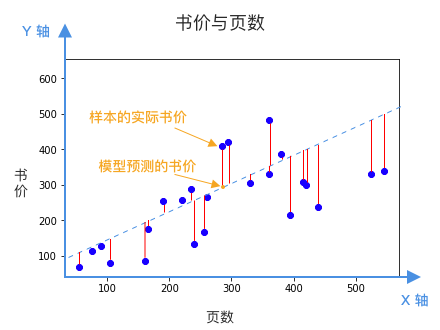
紅線的長度，就是模型（藍色虛線）預測的書價，和樣本書價（藍點）之間的誤差。

紅線的長度等于預測書價和樣本書價的差。以第一個樣本為例，55頁的書，價格69元，所以第一根紅線的長度等于：

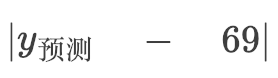
因為絕對值不便于后面的數學推導，我們加個平方，一樣能衡量紅線的長度。

因為我們的預測模型是：

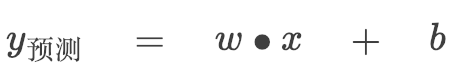
所以

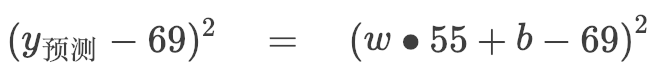
這個樣本是一本 55 頁，69 元的書。

算式開始變得越來越長了，但記住，這都是初中數學而已！前面提到，我們希望所有紅線平均來說越短越好，假設我們有 100 個樣本，用數學來表達就是：

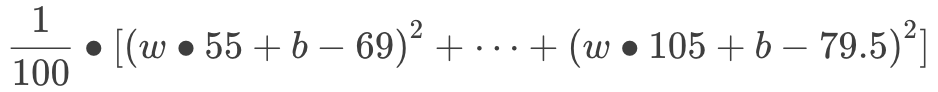
至此，我們把“預測書價”這個問題翻譯成數學語言：“找出 w 和 b 的值，使得以上算式的值最小。”堅持住，第一步馬上結束了！

我們現在有 2 個未知數：w 和 b。為了讓問題簡單一點，我們假設 b 的最佳答案是 0 好了，現在，我們只需要關注 w 這一個未知數：

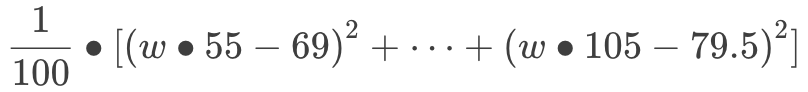
把括號打開：

在機器學習領域，這個方程被稱為“代價 (cost) 函數”，用于衡量模型的預測值和實際情況的誤差。我們把括號全打開：

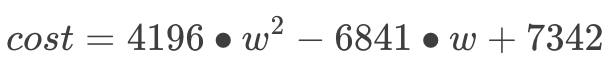
不用在意方程中的數字，都是我瞎掰的。

至此，我們把“預測書價”這個問題翻譯成數學語言：“w 等于多少時，代價函數最小？”第一步完成！到目前為止，我們只用上了初中數學。

—

機器是怎么學習的

代價函數是個一元二次方程，畫成圖表的話，大概會是這樣：

不用在意坐標軸上的具體數字，都是我瞎掰的。

前面講到，機器要找到一個 w 值，把代價降到最低：

機器采取的策略很簡單，先瞎猜一個答案（比如說 w 等于 20 ，下圖紅點），雖然對應的代價很高，但沒關系，機器會用“梯度下降法”不斷改進猜測。

如果你微積分學得很好，此時可能會問：求出導數函數為 0 的解不就完事了嗎？在實際問題中，模型往往包含上百萬個參數，它們之間也并非簡單的線性關系。針對它們求解，在算力上是不現實的。

現在，我們得用上高中數學的求導函數了。針對這個瞎猜的點求導，導數值會告訴機器它猜得怎么樣，小了還是大了。

如果你不記得導數是什么，那就理解為我們要找到一根直線，它和這條曲線只在這一個點上擦肩而過，此前以后，都無交集（就像你和大部分朋友的關系一樣）。所謂的導數就是這根線的斜率。

我們可以看得出，在代價函數的最小值處（即曲線的底部）導數等于 0。如果機器猜測的點，導數大于 0，說明猜太大了，下次得猜小一點，反之亦然。根據導數給出的反饋，機器不斷優化對 w 的猜測。因為機器一開始預測的點導數大于 0 ，所以接下來機器會猜測一個小一點的數：

機器接著對新猜測的點求導，導數不等于 0 ，說明還沒到達曲線底部。

那就接著猜！機器孜孜不倦地循環著“求導 - 改進猜測 - 求導 - 改進猜測”的自我優化邏輯 —— 沒錯，這就是機器的“學習”方式。順便說一句，看看下圖你就明白它為什么叫做“梯度下降法”了。

終于，皇天不負有心機，機器猜到了最佳答案：

就這樣，頭腦簡單一根筋的機器靠著“梯度下降”這一招鮮找到了最佳的 w 值，把代價函數降到最低值，找到了最接近現實的完美擬合點。

總結一下，我們剛剛談論了三件事：

通過觀察數據，我們發現頁數與書價是線性關系——選定模型；

于是我們設計出代價函數，用來衡量模型的預測書價和已知樣本之間的差距——告訴計算機該學習什么；

機器用“梯度下降法”，找到了把代價函數降到最低的參數 w ——機器的學習方法。

機器“深度學習”的基本原理就是這么簡單。現在，我想請你思考一個問題：機器通過這種方法學到的“知識”是什么？

現實問題中的深度學習

為了讓數學推演簡單點，我用了一個極度簡化的例子。現實中的問題可沒那么簡單，主要的差別在于：

現實問題中，數據的維度非常多。

今天在預測書價時，我們只考慮了頁數這一個維度，在機器學習領域，這叫做一個“特征 (feature)”。

但假設我們要訓練機器識別貓狗。一張 200 * 200 的圖片就有 4 萬個像素，每個像素又由 RGB 三個數值來決定顏色，所以一張圖片就有 12 萬個特征。換句話說，這個數據有 12 萬個維度，這可比頁數這一個維度復雜多了。好在，無論有多少個維度，數學邏輯是不變的。

現實問題中，數據之間不是線性關系。

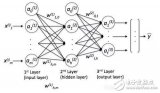
在今天的例子中，頁數和書價之間是線性關系。但你可以想象得到，貓照片的 4 萬個像素和“貓”這個概念之間，可不會是簡單的線性關系。事實上兩者之間的關系是如此復雜，只有用多層神經網絡的上百萬個參數（上百萬個不同的 w：w1, w2, ..., w1000000）才足以表達。所謂“深度”學習指的就是這種多層網絡的結構。

說到這里，我們可以回答前面的問題了：機器所學到的“知識”到底是什么？

就是這些 w。

在今天的例子中，機器找到了正確的 w 值，所以當我們輸入一本書的頁數時，它能預測書價。同樣的，如果機器找到一百萬個正確的 w 值，你給它看一張照片，它就能告訴你這是貓還是狗。

正因為現實問題如此復雜，為了提高機器學習的速度和效果，在實際的開發中，大家用的都是梯度下降的各種強化版本，但原理都是一樣的。