本文作者:格創東智OT團隊(轉載請注明作者及來源)
之前格物匯的文章給大家介紹過,隨著近幾年大數據技術的普及,企業可以獲取海量數據,但是這些海量數據帶給我們更多信息的同時,也帶來了更多的噪音和異常數據,如何降維去噪成為很多企業關注的焦點。而特征抽取和特征選擇都是降維的重要方法,針對于the curse of dimensionality(維數災難),都可以達到降維的目的,但是這兩種方法有所不同。
>>>>
Creatting a subset ofnew features by combinations of the exsiting features.也就是說,特征抽取后的新特征是原來特征的一個映射。
>>>>
特征選擇(Feature Selection)
choosing a subset of allthe features(the ones more informative。也就是說,特征選擇后的特征是原來特征的一個子集。
特征抽取是如何對數據進行變換的呢?其兩個經典的方法:主成分分析(Principle Components Analysis ,PCA)和線性評判分析(LinearDiscriminant Analysis,LDA)給出了解答,今天我們就先來看一下什么是主成分分析。
什么是主成分分析
主成分分析(principal component analysis),PCA是其縮寫。此方法是一種無監督線性轉換技術,其目標是找到數據中最主要的元素和結構,去除噪音和冗余,將原有的復雜數據降維,揭露出隱藏在復雜數據背后的簡單結構。
主成分分析就是試圖在力保數據信息丟失最少的原則下,對這種多變量的數據表進行最佳綜合簡化。這些綜合指標就稱為主成分,也就是說,對高維變量空間進行降維處理,從線性代數角度來看,PCA目標是找到一組新正交基去重新描述得到的數據空間,這些新維度就是主成分。
PCA的原理
我們現在來看一下PCA算法是如何實現的,我們通過一個具體實例來理解,假設我們有這樣一些標準化后的數據:[-1,-2],[-1,0],……,[2,1],[0,1]。我們寫成向量的形式如下:
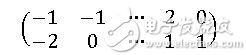
我們還可以在二維坐標系中畫出來:
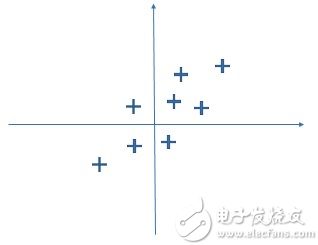
PCA主要的目的是降維簡化數據,這些數據本就是二維,想要再降維則需要重新找一個方向,并把這些點映射到這個方向上(降到1維)。試想,怎么才能找到這個方向,且不損失大部分信息呢?PCA的做法是,找到新映射的方法需要滿足如下兩個原則:
在新映射的方向上每個數據的映射點方差盡可能大。因為方差大的數據所包含的信息量越大。
新映射的方向應彼此正交,這樣映射出的坐標點選取才更有意義。
尋找新映射也可以看作基變換,我們可以不斷旋轉基,尋找滿足上面兩個原則的情況。如下圖所示,中間的映射方向圖里數據在新基上映射點的方差就比右邊圖映射點方差大的多。而方差大則表示該數據在該方向上含有的信息量多,反之另一個新基的方向上含有的信息量就少的多。如果這個方向上的信息量非常少,即使舍去也無傷大雅,我們就可以考慮將其舍去,實現降維的操作。
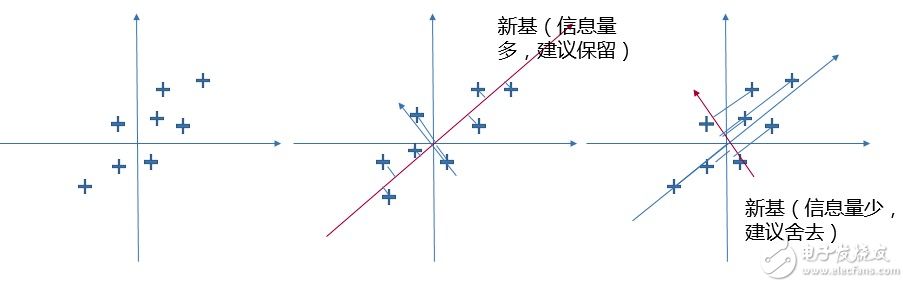
新基可以看成是由以前標準直角坐標系旋轉而成,在線性代數中,這樣的坐標軸旋轉操作可以通過原本直角坐標系坐標乘轉換矩陣得到:
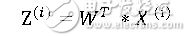
所以我們就將問題轉換成找轉移矩陣W上,如何去求W呢?我們希望降維后的數據要盡可能的與原數據非常接近(不丟失信息)。我們可以計算轉換后的坐標Z與轉換之前的坐標X之間的距離:
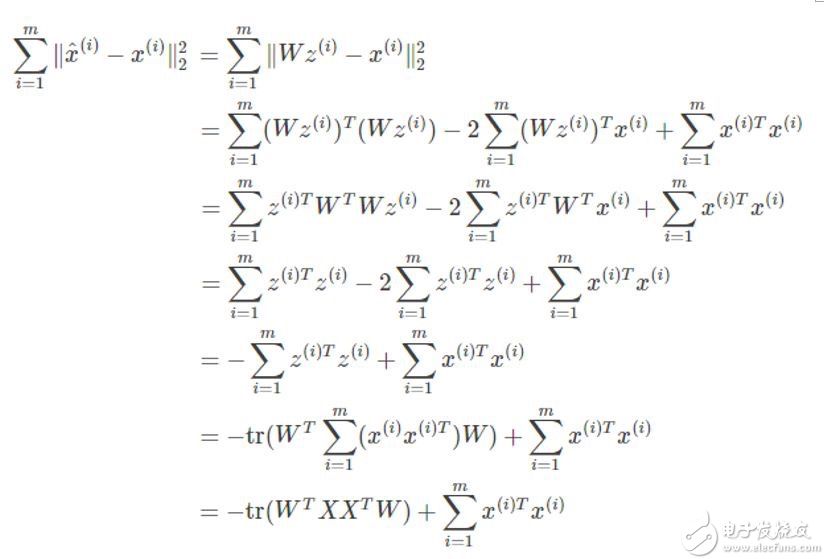
因此為了讓轉換距離最小,我們可以將問題等價轉換成:
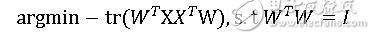
由于中間推導過程較為復雜,故在此省略,最后求解推導的結果為:
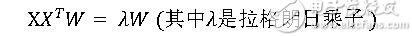
這不正是特征值的定義公式嗎?所以只需要對協方差矩陣進行特征值分解,并將求得的特征值排序,取前N(PCA所要降低的目標維度)個特征值構成的向量W,即為PCA的解。
PCA優缺點
優點
(1)它是無監督學習,只與數據相關,無參數限制。
(2)通過PCA降維,可以達到簡化模型和對數據進行壓縮的效果。同時最大程度的保持了原有數據的信息。
(3)各主成分之間正交,可消除原始數據成分間的相互影響。
(4)計算方法簡單,易于在計算機上實現。
缺點
(1)如果用戶對觀測對象有一定的先驗知識,掌握了數據的一些特征,卻無法通過參數化等方法對處理過程進行干預,可能會得不到預期的效果,效率也不高。
(2)貢獻率小的主成分往往可能含有對樣本差異的重要信息。
好了,今天格物匯的內容就到這里,近期我們還將介紹特征抽取的另一種方法LDA(線性評判分析),敬請期待。
-
智能制造
+關注
關注
48文章
5571瀏覽量
76380 -
工業互聯網
+關注
關注
28文章
4323瀏覽量
94149
發布評論請先 登錄
相關推薦
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+內容簡介
ADS1299用ADS采集數據,ADS可以不抽取看原始得數據嗎?
求助,關于AMC1306M25抽取率OSR的疑問求解
求助,AD7190關于Σ-Δ ADC其中的抽取濾波器的數據轉換問題求解
圖像識別算法的核心技術是什么
使用rtthread settings配置完i2c后,與pca9535pw的第一通訊報錯,為什么?
PCA9655E I / O端口擴展器 I

機器學習的經典算法與應用

簡單認識變頻器和PLC/PCA系統
ICY DOCK Expresscage MB038SP-B硬盤抽取盒評測





 淺析特征抽取的經典算法PCA
淺析特征抽取的經典算法PCA












評論