Trie這個名字取自“retrieval”，檢索，因為Trie可以只用一個前綴便可以在一部字典中找到想要的單詞。

雖然發音與「Tree」一致，但為了將這種 字典樹 與 普通二叉樹 以示區別，程序員小吳一般讀「Trie」尾部會重讀一聲，可以理解為讀「TreeE」。

Trie 樹，也叫“字典樹”。顧名思義，它是一個樹形結構。它是一種專門處理字符串匹配的數據結構，用來解決在一組字符串集合中快速查找某個字符串的問題。

此外 Trie 樹也稱前綴樹（因為某節點的后代存在共同的前綴，比如pan是panda的前綴）。

它的key都為字符串，能做到高效查詢和插入，時間復雜度為O(k)，k為字符串長度，缺點是如果大量字符串沒有共同前綴時很耗內存。

它的核心思想就是通過最大限度地減少無謂的字符串比較，使得查詢高效率，即「用空間換時間」，再利用共同前綴來提高查詢效率。

Trie樹的特點

假設有 5 個字符串，它們分別是：code，cook，five，file，fat。現在需要在里面多次查找某個字符串是否存在。如果每次查找，都是拿要查找的字符串跟這 5 個字符串依次進行字符串匹配，那效率就比較低，有沒有更高效的方法呢？

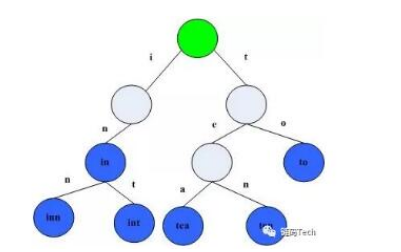
如果將這 5 個字符串組織成下圖的結構，從肉眼上掃描過去感官上是不是比查找起來會更加迅速。

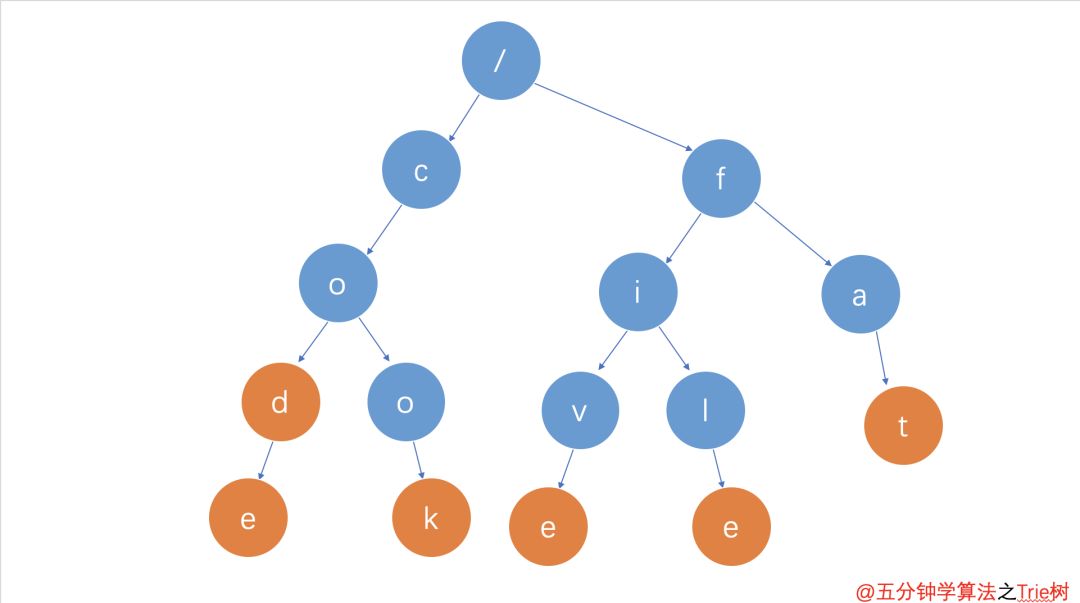
Trie樹樣子

通過上圖，可以發現 Trie樹 的三個特點：

根節點不包含字符，除根節點外每一個節點都只包含一個字符

從根節點到某一節點，路徑上經過的字符連接起來，為該節點對應的字符串

每個節點的所有子節點包含的字符都不相同

通過動畫理解 Trie 樹構造的過程。在構造過程中的每一步，都相當于往 Trie 樹中插入一個字符串。當所有字符串都插入完成之后，Trie 樹就構造好了。

Trie 樹構造

Trie樹的插入操作

Trie樹的插入操作

Trie樹的插入操作很簡單，其實就是將單詞的每個字母逐一插入 Trie樹。插入前先看字母對應的節點是否存在，存在則共享該節點，不存在則創建對應的節點。比如要插入新單詞cook，就有下面幾步：

插入第一個字母c，發現root節點下方存在子節點c，則共享節點c

插入第二個字母o，發現c節點下方存在子節點o，則共享節點o

插入第三個字母o，發現o節點下方不存在子節點o，則創建子節點o

插入第三個字母k，發現o節點下方不存在子節點k，則創建子節點k

至此，單詞cook中所有字母已被插入 Trie樹 中，然后設置節點k中的標志位，標記路徑 root->c->o->o->k 這條路徑上所有節點的字符可以組成一個單詞cook

Trie樹的查詢操作

在 Trie 樹中查找一個字符串的時候，比如查找字符串 code，可以將要查找的字符串分割成單個的字符 c，o，d，e，然后從 Trie 樹的根節點開始匹配。如圖所示，綠色的路徑就是在 Trie 樹中匹配的路徑。

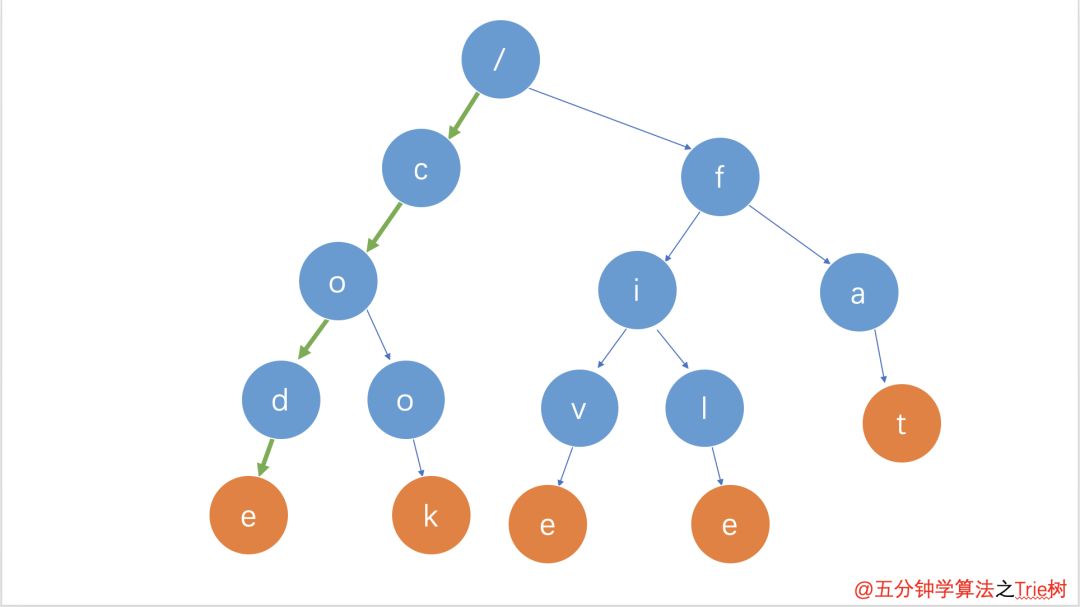
code的匹配路徑

如果要查找的是字符串 cod(鱈魚)呢？還是可以用上面同樣的方法，從根節點開始，沿著某條路徑來匹配，如圖所示，綠色的路徑，是字符串 cod 匹配的路徑。但是，路徑的最后一個節點「d」并不是橙色的，并不是單詞標志位，所以 cod 字符串不存在。也就是說，cod是某個字符串的前綴子串，但并不能完全匹配任何字符串。

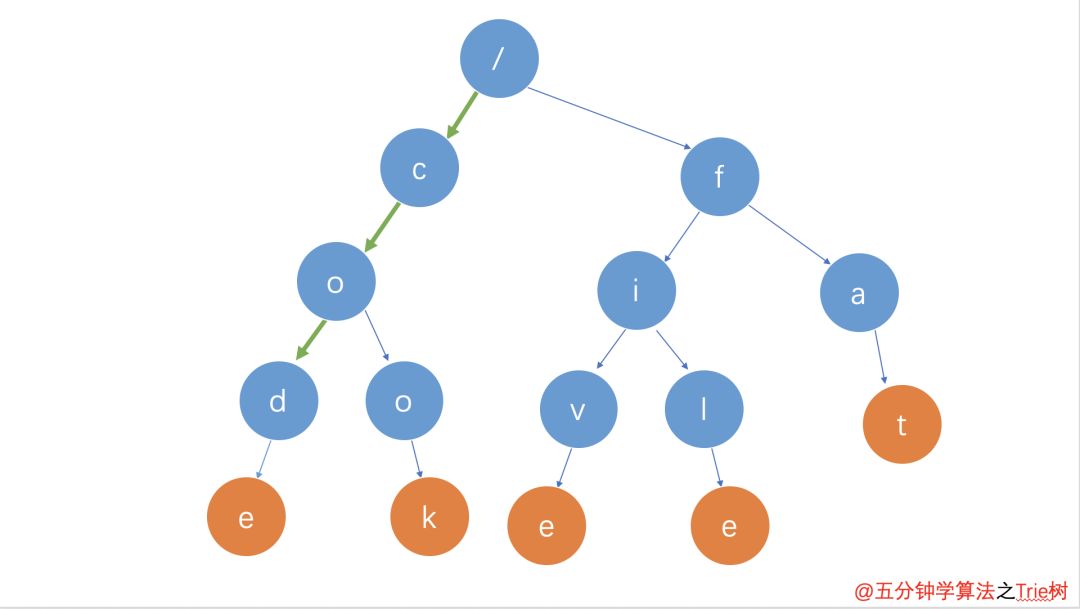
cod的匹配路徑

程序員不要當一條咸魚，要向 cook 靠攏：）

Trie樹的刪除操作

Trie樹的刪除操作與二叉樹的刪除操作有類似的地方，需要考慮刪除的節點所處的位置，這里分三種情況進行分析：

刪除整個單詞（比如hi）

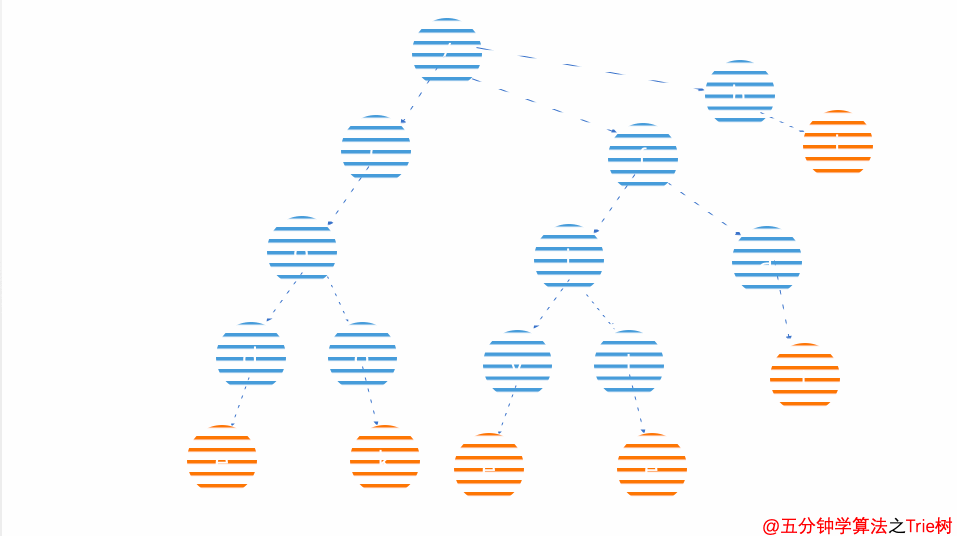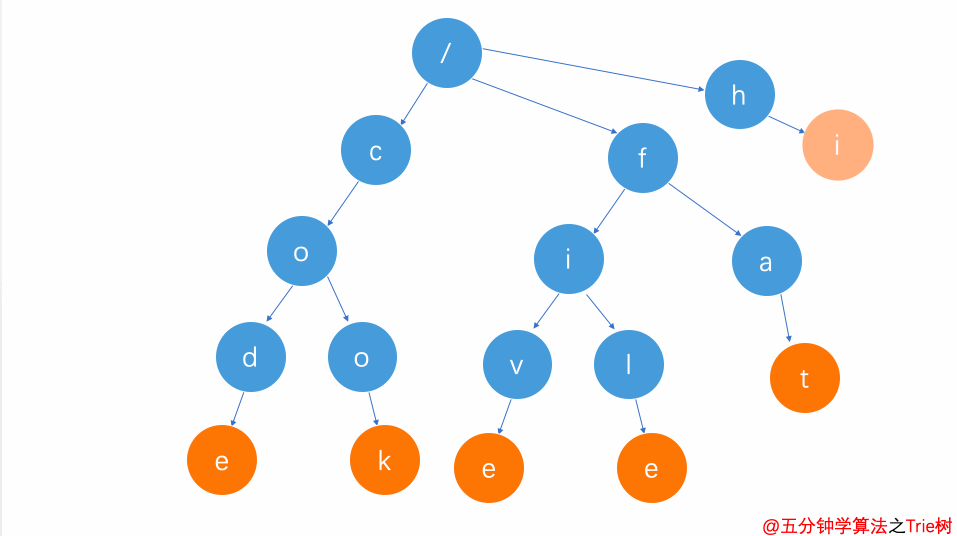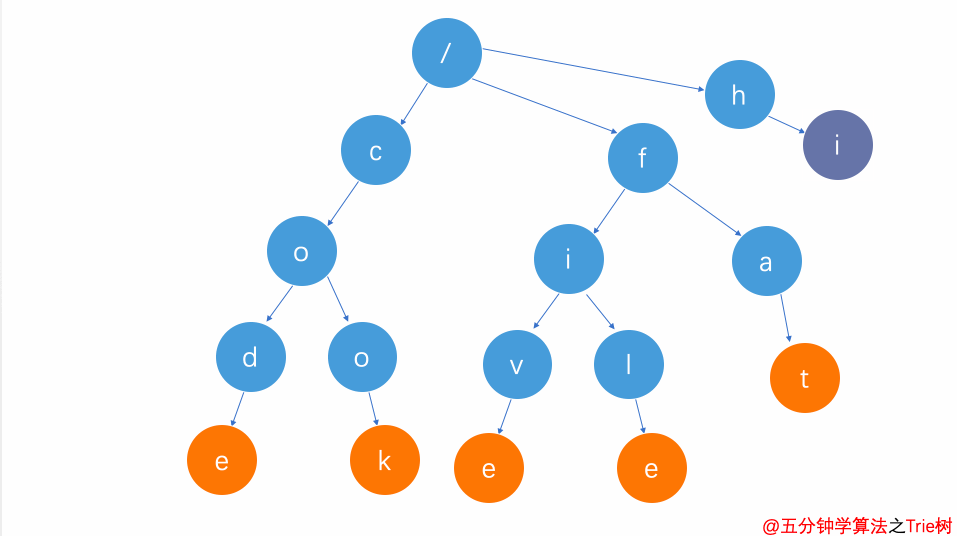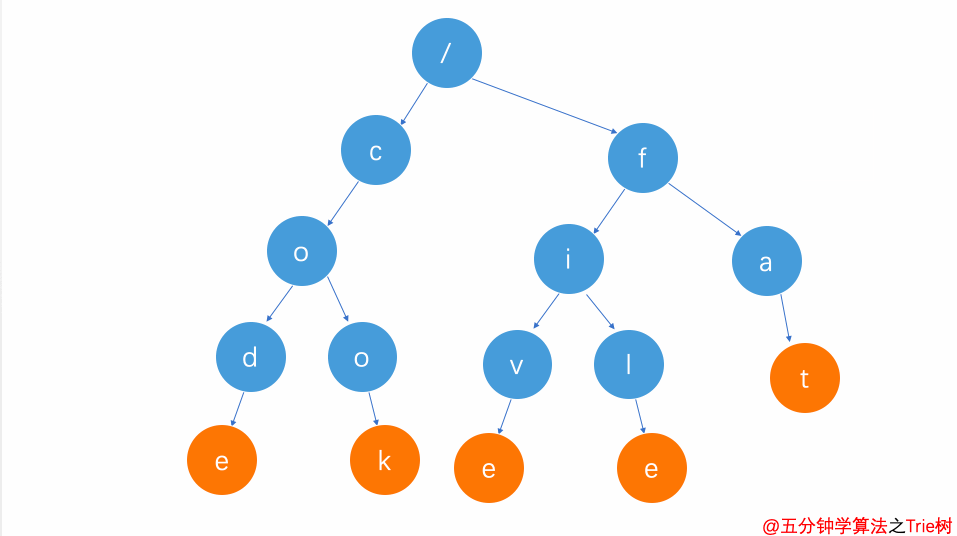
刪除整個單詞

從根節點開始查找第一個字符h

找到h子節點后，繼續查找h的下一個子節點i

i是單詞hi的標志位，將該標志位去掉

i節點是hi的葉子節點，將其刪除

刪除后發現h節點為葉子節點，并且不是單詞標志位，也將其刪除

這樣就完成了hi單詞的刪除操作

刪除前綴單詞（比如cod）

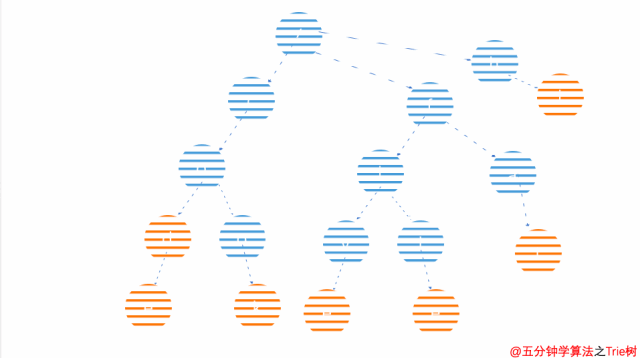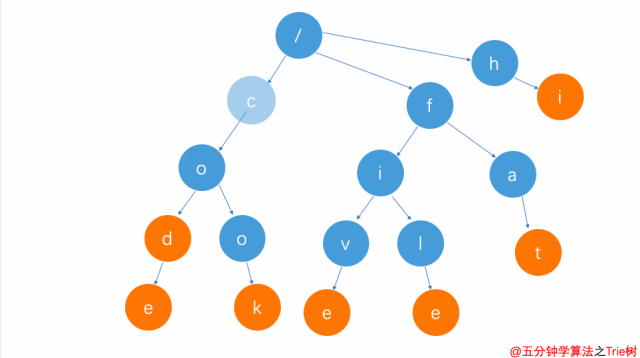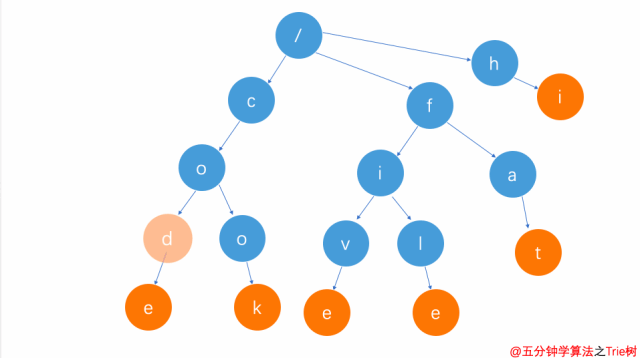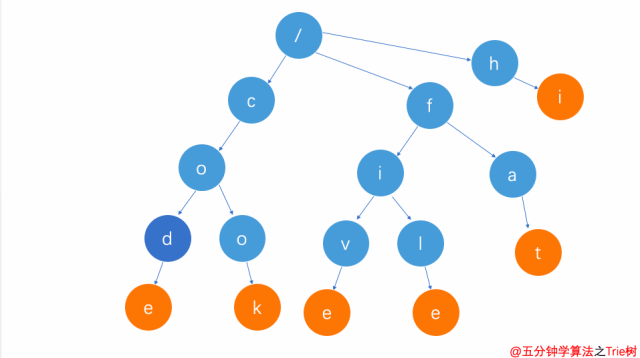
刪除前綴單詞

這種方式刪除比較簡單。

只需要將cod單詞整個字符串查找完后，d節點因為不是葉子節點，只需將其單詞標志去掉即可。

刪除分支單詞（比如cook）

刪除分支單詞

與刪除整個單詞情況類似，區別點在于刪除到cook的第一個o時，該節點為非葉子節點，停止刪除，這樣就完成 cook 字符串的刪除操作。

Trie樹的應用

事實上 Trie樹 在日常生活中的使用隨處可見，比如這個：

具體來說就是經常用于統計和排序大量的字符串（但不僅限于字符串），所以經常被搜索引擎系統用于文本詞頻統計。它的優點是：最大限度地減少無謂的字符串比較，查詢效率比哈希表高。

1. 前綴匹配

例如：找出一個字符串集合中所有以 五分鐘 開頭的字符串。我們只需要用所有字符串構造一個 trie樹，然后輸出以 五?>分?>鐘 開頭的路徑上的關鍵字即可。

trie樹前綴匹配常用于搜索提示。如當輸入一個網址，可以自動搜索出可能的選擇。當沒有完全匹配的搜索結果，可以返回前綴最相似的可能。

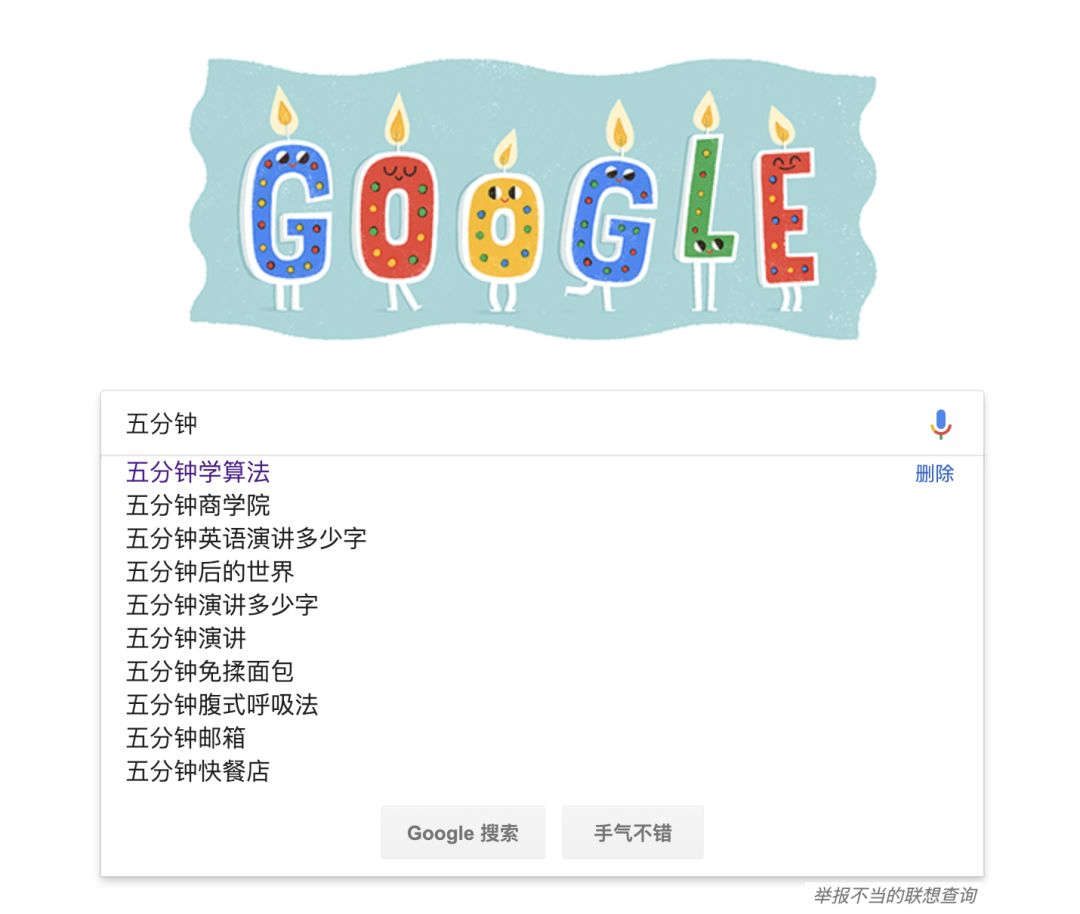
google搜索

2. 字符串檢索

給出 N 個單詞組成的熟詞表，以及一篇全用小寫英文書寫的文章，按最早出現的順序寫出所有不在熟詞表中的生詞。

檢索/查詢功能是Trie樹最原始的功能。給定一組字符串，查找某個字符串是否出現過，思路就是從根節點開始一個一個字符進行比較：

如果沿路比較，發現不同的字符，則表示該字符串在集合中不存在。

如果所有的字符全部比較完并且全部相同，還需判斷最后一個節點的標志位（標記該節點是否代表一個關鍵字）。

Trie樹的局限性

如前文所講，Trie的核心思想是空間換時間，利用字符串的公共前綴來降低查詢時間的開銷以達到提高效率的目的。

假設字符的種數有 m 個，有若干個長度為n的字符串構成了一個 Trie 樹 ，則每個節點的出度為 m（即每個節點的可能子節點數量為 m），Trie 樹的高度為 n。很明顯我們浪費了大量的空間來存儲字符，此時 Trie 樹的最壞空間復雜度為 O(m^n)。也正由于每個節點的出度為 m，所以我們能夠沿著樹的一個個分支高效的向下逐個字符的查詢，而不是遍歷所有的字符串來查詢，此時 Trie 樹的最壞時間復雜度為 O(n)。

這正是空間換時間的體現，也是利用公共前綴降低查詢時間開銷的體現。