拓撲排序是算法課經典內容之一,但是學的時候如果只是被動接收,那就很容易淪為“算法背誦”,很快就記憶模糊了。這一次同樣的,我們從主動發明的出發點去搞清楚這個問題的機理,就很難遺忘了。
跟上回一樣,從發明的角度,我們只要問兩點:
(1) 我們想解決一個什么問題?
(2) 這個問題如何最好地解決?
1
動機:前提關系
本文中我們想解決的各種問題,都有一個明確的共同范式:任務,和任務之間的先后順序,或者說前提關系。有很多任務需要完成,其中有的任務開始之前,會要求某些前提任務首先被完成。
這樣的具體例子很常見,生活中比如
先修課程:一系列課程,基礎課可以隨便修,想上稍微高級一點的課程可能會要求先修完若干門基礎一點的課程。在這樣“先修課程”的關系之下,怎么把一系列課全修完,就需要在順序上有一些計劃
計算機內部這樣的情形更常見,比如:
軟件包批量安裝:安裝很多軟件包的時候,有的包會用到別的包,被用到就要先裝,安裝器就需要根據這些前提關系規劃安裝順序
計算任務:設置復雜的計算任務的時候,有的計算需要用到別的計算的結果,計算框架的scheduler就需要理清這里面隱含的先后關系,才能所有結果全算出來
2
問題
所以,對這個問題合理的抽象就是,有任務,也有任務之間的依賴關系,它們之間自然會形成一個dependency graph:
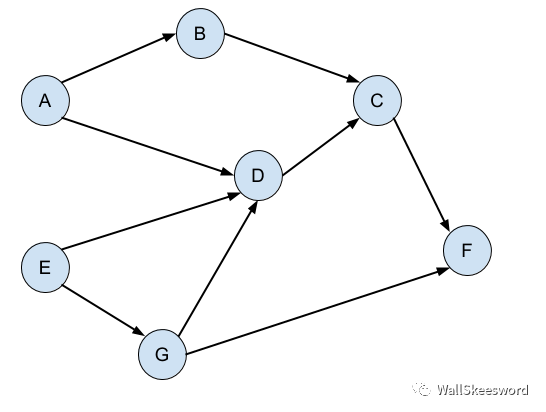
而我們想找出一種合理的任務順序,按這個順序依次完成任務,可以保證做到每件任務的時候,它的前提任務都已經被完成。上圖中,比如 A-B-E-G-D-C-F。
3
徒手體會
先徒手操作一下,對這個問題產生一些最直觀認識。其實對于人來說,這個問題沒什么難度,大可以邊做邊想。比如當你面對一堆課程的時候(例子來源于本人將在程序員末日2038年胡亂編纂的“從入門到放棄”系列精品課程)
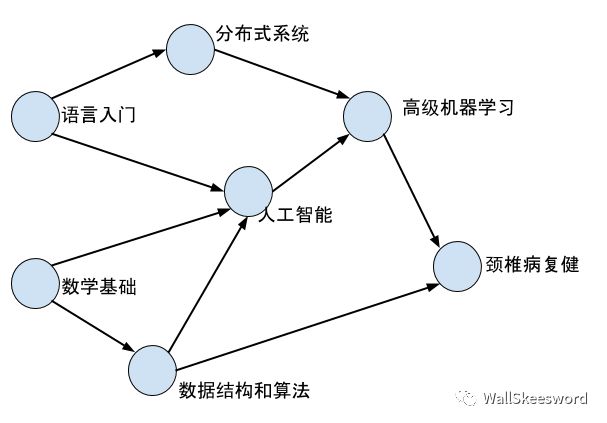
首先總該有一些課是直接可以上的,比如圖中“語言入門”和“數學基礎”。你完全可以選一門上就好了,比如你選“數學基礎”,上完之后這門就可以拋到腦后
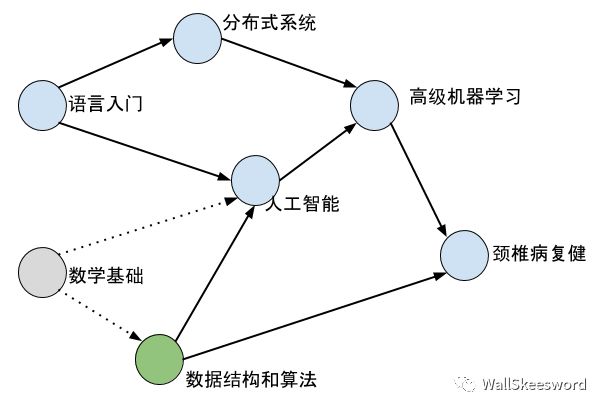
順便這也有可能為新的課打開了大門,比如現在就新可以上“數據結構和算法”了。所以直覺來看拓撲排序并沒有什么難度,只要有耐心,誰都可以一步步順著當前可以上的課上,成功地從入門到放棄(誤)。
4
初步解法
那么其實我們就已經可以有一個最原始的解法了,非常簡單粗暴,但是至少可以給出正確的答案:每次重新審視這個圖,一個一個檢查還沒完成的任務,如果哪一個任務的所有前提都已完成,下一個就做它,也就是,加入輸出序列,并把這個新任務標記為完成。舉例說明,比如說當你做到某一步時,來到了下圖所示的這個情境中(灰色為已完成任務, 丑藍為待完成任務)
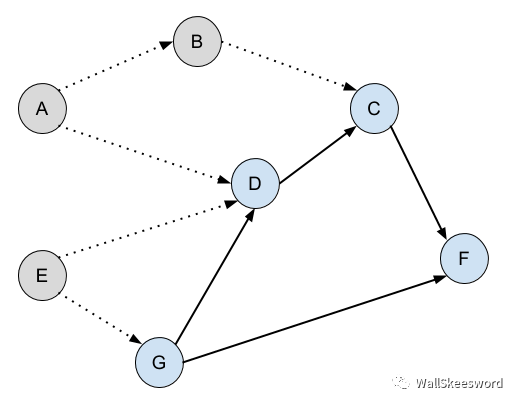
你可以一個個檢查有待完成的藍色任務們。C,它還有前提任務D沒有完成;D在等G;F也不行;G,誒,它的前提任務都已完成,好,那就它了。下一個輸出G,并且把它標為已完成。
如此往復,最終總能把所有任務都有條不紊地完成。
作為最原始的解法,它的效率不高。但是這并沒有關系,找到其中的浪費,一個個解決,自然就可以迭代出一個好的解法。
5
優化:去掉浪費
浪費1
首先,“檢查前提任務有沒有都完成”這個步驟,可以簡潔一點。每個結點可以一直記著自己還有幾個前提任務沒有完成(結點的入度)。比如下圖,藍色數字標注還剩幾個前提任務
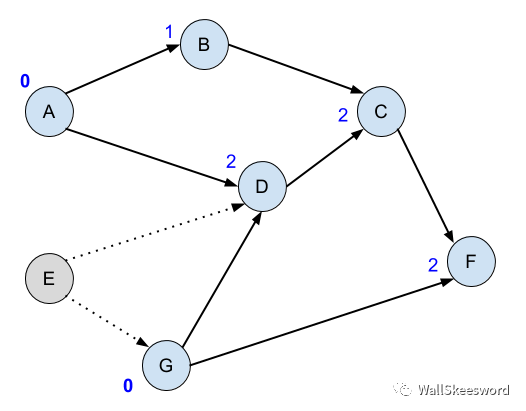
接下來,如果我們完成了A,可以去通知它的后繼結點們 B 和 D,告訴它們入度可以減1了。這樣,你只要看一個任務的未完成前提數有沒有降到0,就知道這個任務是不是可做。
浪費2
我們的流程還有一個巨大的浪費:我們在重復尋找已ready(入度為0)的結點。接著 ↑上圖↑ 的情形,我們發現A和G已經入度為0,處于ready狀態;假設我們接下來選擇做A,于是 B 和 D 入度減1:
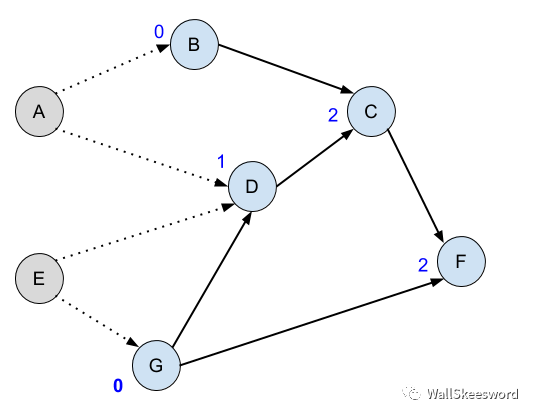
然后下一輪的時候,我們還需要遍歷所有藍色結點,去尋找那些ready的嗎?不需要:
我們上一輪就知道G的入度為0的,現在肯定沒變過
只有 A 的后繼 B 和 D 的入度發生了下降,其他的 C 和 F 這些結點完全沒受影響,那它們的入度既然之前不是0,現在沒變,肯定依然不是0
所以說,我們記著之前發現過的所有ready的結點,然后每次只需要在那些入度被更新的結點中尋找新的ready結點就夠了。如此一來,我們去掉了大量的浪費,也得出了一個算法了——
維護一個所有ready結點組成的集合,每次從里面選一個結點完成,把它的后繼的入度都減一,并在被更新的結點中找出新的ready結點,加入我們的集合。
6
標準解法 BFS
這樣子迭代優化出來的做法,其實就是拓撲排序所謂的BFS解法。我們用具體的例子直觀地描述一遍。
初始化的時候,計算每個結點的入度,所有初始入度就為0的結點,都是處于ready狀態的任務,加入我們的集合(圖中標為丑綠)
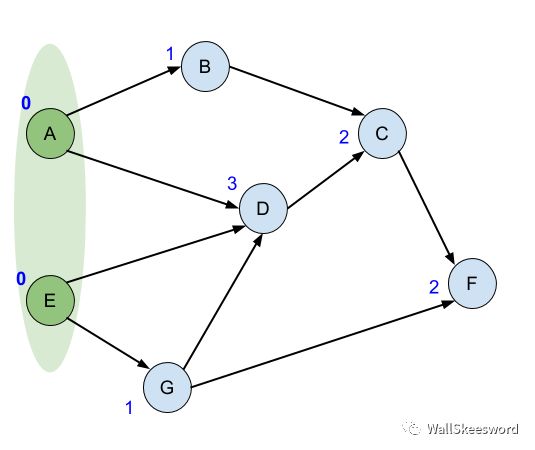
接下來每一次,從綠色ready集里面隨便拿一個結點出來,比如 A,這個任務已經處于ready狀態,所以完成它(輸出);A任務完成以后,它的后繼結點 B 和 D 的入度都可以去掉 1,如果有哪個后繼結點在這個過程中入度降成了0 (比如B),那它也進入了ready狀態,我們就順手把它加入我們的ready集合。
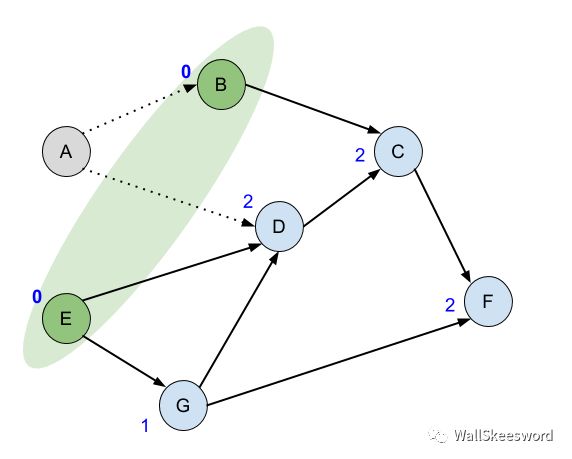
如此這般,循環下去,每次找到下一個可以做的任務,可以一路把拓撲排序輸出出來。
圖看完了,再用迷幻的偽代碼描述一下:
初始化1:每個結點把自己的入度數好[乖巧]初始化2:建立一個ready集合,記錄下哪些結點已經ready.把一開始入度就為0的源點都加入集合接下來只要集合里還有結點: 1. 從集合里隨便拿一個結點v出來 2. 把v輸出,并且通知它的所有后繼:你們的前提任務又少了一個,快把入度-1 3. 在順序通知的同時,如果哪個后繼發現自己的前提任務因此全部達成(入度降到0),就把自己加入ready大家庭如此往復,就獲得了這個圖的一個拓撲排序。
這樣一來,這個循環中,每條邊都正好被用到一次(為什么?),浪費已經降到最小,我們知道已經達到效率最優解了。
7
標準解法 DFS:目標導向
我很久以前首次接觸這個問題的時候,發明的就是上面BFS的解法,因為它符合事物自然推進的順序,“撿當前能做的東西做”。一直到大學的時候我才知道,原來有簡便得多的方法,雖然理論復雜度相同,但想起來、寫起來都要簡潔很多,這就是拓撲排序的所謂DFS解法。非常有意思的是,這個解法來自于“從目標出發,一步步倒推”的結果導向型思路。
怎么說呢,就是面對一個dependency graph,我不是循序漸進撿ready的任務做,而是隨手指一個結點,比如下圖中的 “一個億”

然后先將其確立一個小目標,別的什么都不想,只求完成我指定的這個任務。確立“一個億”小目標之后,就要開始倒推了,為了能完成任務“一個億”,我得先完成它的所有前提,就是“悔創阿里”和“不知妻美”,于是乎對于每一個前提任務,你也可以同樣倒推(比如為了達成成就“不知妻美”,首先要做任務“普通人家”),依次去滿足他們的前提條件,一直到倒推到沒有前提的任務,或者之前已經完成的任務為止。
這個自我重復的流程非常適合遞歸。直接上迷幻的偽代碼,大家感受一下它簡潔的魅力
(所有結點上都應該有個標記,標該結點是否已完成/輸出過)function完成小目標(v):先看看v之前有沒有被完成過1.已完成→打擾了,return2.未完成→好的,干它a)對于v的所有前提任務ui:遞歸調用完成小目標(ui)b)都完成之后,現在所有前提應該都已滿足,就輸出v,并標記為已完成
當然,為了獲得全圖的拓撲排序,我們還需要一個粗暴的循環——
對于圖中所有結點v:調用完成小目標(v)
建議初次接觸的朋友自己試幾個結點感受一下,遞歸函數所倚靠的系統棧,如何就幫你把這個順序問題全部解決了。
8
思考:環
以上我們就介紹完了兩種常見的拓撲排序算法。
但是接觸過這個問題的人都知道,對于一個有向圖,首先拓撲排序是否存在都得打個問號。之前的討論中我刻意忽略了這個問題,因為對于初學者來說,同時操心太多頭緒可能會干擾思考。現在,是時候把這個問題重新加入考慮,正好也作為對之前內容的進一步思維練習。
問題:拓撲排序什么時候根本就不存在呢?
當然,舉出一個沒有拓撲排序的例子不難——當兩個任務直接或間接互為前提條件的時候,就沒法完成了,比如:
這些時候,圖中都有一個“環”的存在,循環調用,互為前提。
有環就沒法拓撲排序,這個比較好理解。反過來的方向,有向圖如果沒有環就一定有拓撲排序,需要稍微數學一點的證明,為了保持本文的flow,就跳過留給有興趣的人自己想了。
于是乎,我們有結論,拓撲排序一定建立在“有向無環圖”之上。那么怎么在算法中檢查環的存在呢?也就是說,我們面對的問題變得更一般了一些,現在任務不是給定有向無環圖,找出一個拓撲排序,而是:
給定一個有向圖,輸出拓撲排序,或者判定圖中有環。
BFS解法中加入判斷
回顧一下剛才的BFS解法,我們是用一個集合/容器記著所有目前已經ready的結點,每次取出一個,輸出,然后在它的后繼中尋找新的ready結點加入集合。那么想象在一個有環的圖中會出現什么呢?
沒想明白的盆友可以先自己演繹一下。
。
。
。
。
。
。
。
如果在我們之前的圖中,將DE之間的邊反向,則會出現圖中紅色標注的環。
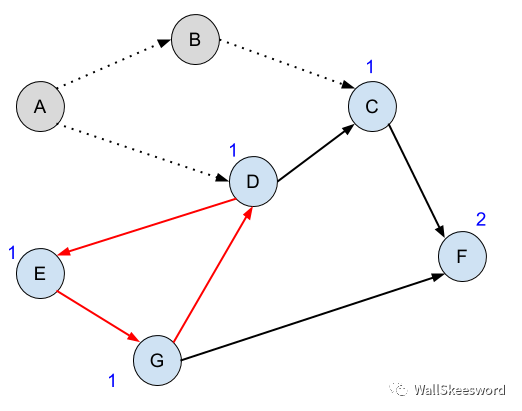
按照之前的方法運行我們的BFS算法,可以成功完成A,然后B,之后會卡在圖中所示的尷尬境地:沒有入度為0的結點了,所有未完成任務都要求別的任務先完成,誰也不讓誰,于是我們卡在這里再也進行不下去。
所以這就是BFS中我們判斷環的標準:如果算法進行到某一步,還有未完成任務,但ready集合為空,即沒有任務是ready的,則一定是有環把我們卡住了。
DFS解法中加入判斷
如果DFS解法遇到了有環的情況,會發生什么?如果還是用上圖的紅色環為例,為了完成D,你會調用如下序列
完成小目標(D)
→ 完成小目標(A),
完成小目標(G)
→ 完成小目標(E)
→ 完成小目標(D)
→ ...
你會發現這個遞歸進入一個死循環。所以判斷圖中有沒有環的方法,就是想辦法去發現自己的遞歸流程有沒有重復訪問同一個結點。但這其中有一些細節需要思考,比如其實訪問一個已訪問過的結點很多時候也是正常的——結點被訪問過可能是因為被之前某個任務完成了。所以可能需要我們想辦法區分這兩種情形。這是一個很有意思的問題,自己想明白會很有趣,所以我們照例在最后留一點想象空間,由有興趣朋友自己思考品玩 :)
-
拓撲
+關注
關注
4文章
341瀏覽量
29616 -
計算機
+關注
關注
19文章
7508瀏覽量
88070 -
DFS
+關注
關注
0文章
26瀏覽量
9172
原文標題:拓撲排序
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
TimSort:一個在標準函數庫中廣泛使用的排序算法
CAN總線十萬個為什么 | 聊聊幾種常見的CAN網絡拓撲

時間復雜度為 O(n^2) 的排序算法

設計一個電源,如何考慮選擇拓撲?
儲能變流器的拓撲結構介紹
FPGA實現雙調排序算法的探索與實踐





 拓撲排序的介紹和如何使用拓撲排序解決一個問題
拓撲排序的介紹和如何使用拓撲排序解決一個問題














評論