在格物匯之前的文章中，我們系統性的介紹了特征抽取的經典算法——主成分分析PCA與線性判別分析LDA的原理、應用場景，以及這兩種算法的局限性和改進方法。今天的格物匯要給大家介紹一種新的機器學習算法——流形學習。

流形學習

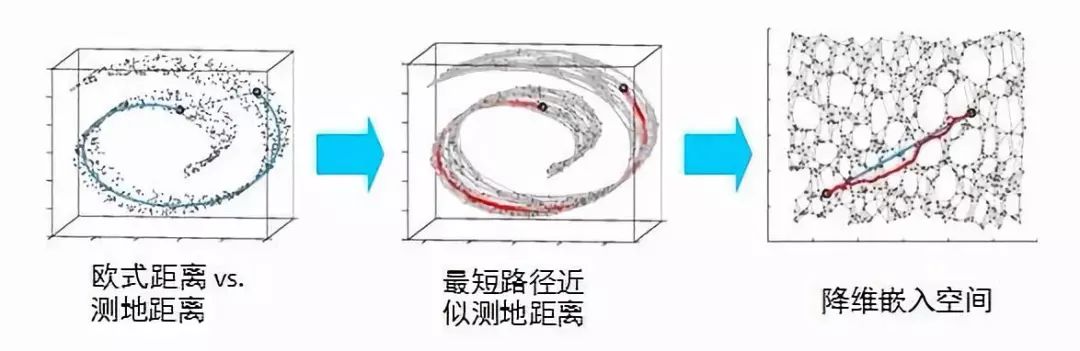
流形學習是一類借鑒了拓撲流形概念的降維方法，與核PCA的目的一樣，它想要在低維空間中盡量保持在高維空間中的結構。一個形象的流形降維過程如下圖，我們有一塊卷起來的布，我們希望將其展開到一個二維平面，我們希望展開后的布能夠在局部保持布結構的特征，其實也就是將其展開的過程，就像兩個人將其拉開一樣。

流形學習方法有很多種，但是他們具有一些共同的特征：首先構造流形上樣本點的局部鄰域結構，然后用這些局部鄰域結構來將樣本點全局的映射到一個低維空間。它們之間的不同之處主要是在于構造的局部鄰域結構不同，以及利用這些局部鄰域結構來構造全局的低維嵌入方法的不同。下面我們簡要介紹兩種最常見的流形學習方法：Isomap和LLE。

Isomap

高維數據結構可能太過于抽象，很難去理解。我們先來看一個具體的實例：在上一篇文章中，我們所看到的三維空間上的數據是呈現”S”型，假設我們想尋找圖中兩點的測地距離（延曲面距離），就不能用這兩點坐標所計算的歐式距離，如下圖（a）黑色線所示，因為黑色線所構成的路徑延曲面不可達。而應該使用其沿著“S”形曲面所生成的距離，想象一下一只螞蟻在數據曲面上爬行，它不能脫離曲面行走，行走的路徑如下圖（a）紅色線所示。下圖（b）則顯示的是兩條線本真二維結構上所顯示的路徑，很明顯紅色的線更加真實的反映了兩個數據點在三維數據上的距離。

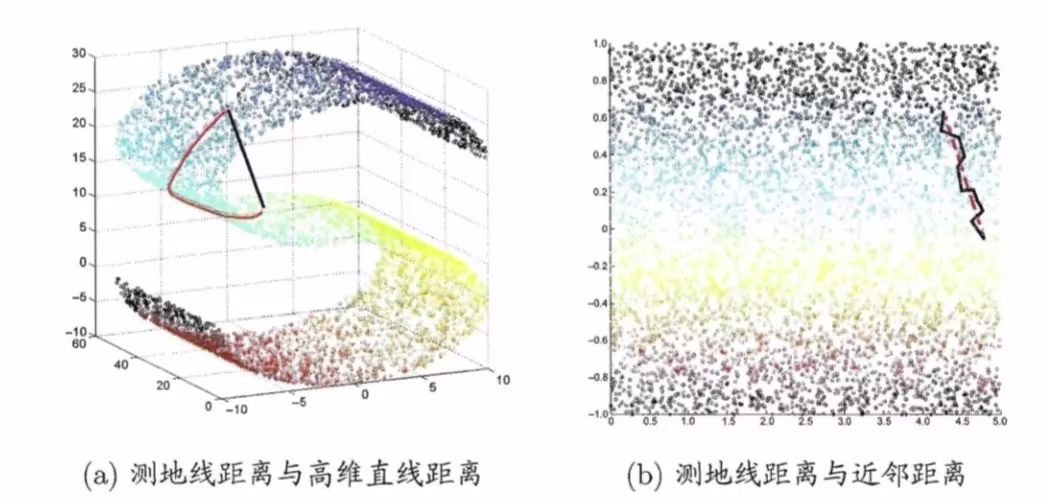
上述這種尋找數據曲面測算距離的方法稱為Isomap（等度量映射），它是流形學習中的一種方法。它是如何實現的呢？它假設數據點與K個最近鄰的點可以構成一個子集，這個子集可以用普通的歐式距離來衡量，而這個子集中的點又與其他子集中的點相連，這樣兩個目標點的距離就可以分解成若干子集的歐式距離疊加來近似得到，最后這些相連的點可以降維到低維空間中展現出來。

局部線性嵌入（LLE）

流形學習另外一個典型案例是局部線性嵌入（LLE）。Isomap假設近鄰的測地距離可以用歐式距離來表示。而LLE則假設在近鄰內可以用線性加權互相表達。比如對于任意一個樣本x0，我們都可以用他附近的幾個點x1 x2 x3 x4的線性組合表示出來，即

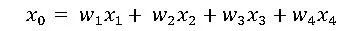
經過LLE降維投影后，原來的點x0 x1 x2 x3 x4，投影變成了

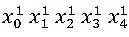
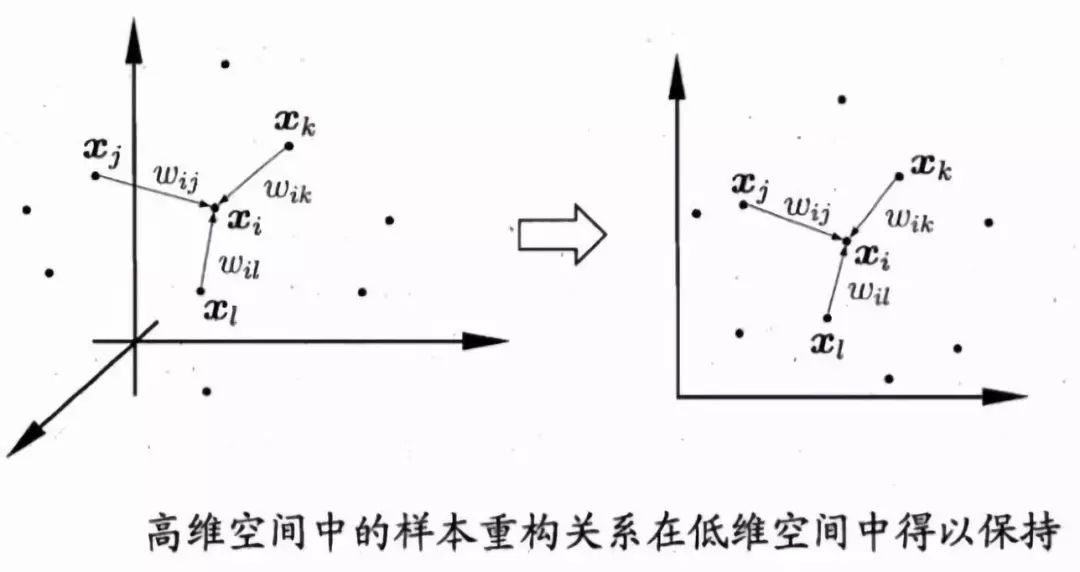
LLE降維的想法是，降維后盡量去保留高維時的線性組合關系：

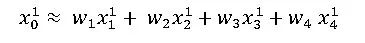
如何求解呢？我們需要先求出線性組合的權重w，對于樣本x0我們需要找到其最近的k個其他樣本點，假設為x1 x2 x3 x4，我們根據線性表示誤差最小來求出w：

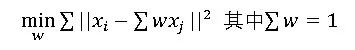
根據上式確定出線性組合的w以后，我們還需要讓其在低維空間也能盡可能滿足線性組合的表達關系式，也就是說對于x0 x1 x2 x3 x4……的低維投影點z0 z1 z2 z3 z4……滿足：

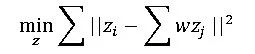
兩個優化目標函數類型很像，但需要明確的是第一個目標函數優化的是權重w，而第二個目標函數優化的是降維后的坐標z。經過優化即可得出樣本集在低維空間上的投影坐標。

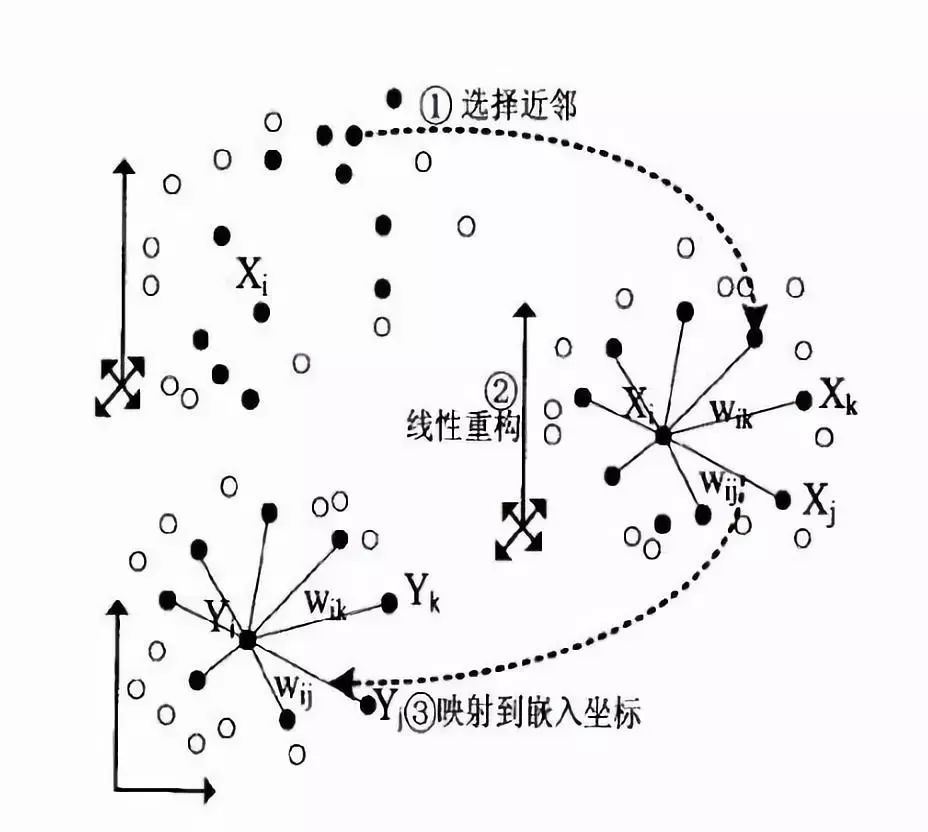
總的來說，對于不在某一個點x0鄰域內的其他點A，不管A怎么變動，都不會影響到點x0，這種變動局部限制的思想在很多地方都有用，此外LLE盡可能的保存了局部線性信息，使得其在局部能反映出數據原本的結構。它的流程大致如下圖所示：

小結

LLE是廣泛使用的圖形圖像降維方法，它實現簡單，但是對數據的流形分布特征有嚴格的要求。比如不能是閉合流形，不能是稀疏的數據集，不能是分布不均勻的數據集等等，這限制了它的應用。

優點

1、可以學習任意維的局部線性的低維流形

2、算法歸結為稀疏矩陣特征分解，計算復雜度相對較小，實現容易

缺點

1、算法所學習的流行只能是不閉合的，且樣本集是稠密均勻的

2、算法對最近鄰樣本數的選擇敏感，不同的最近鄰數對最后的降維結果有很大影響