無(wú)論是提供商品還是服務(wù)，用戶畫像都是數(shù)據(jù)挖掘工作的重要一環(huán)。一個(gè)準(zhǔn)確和完整的用戶畫像甚至可以說是許多互聯(lián)網(wǎng)公司賴以生存的寶貴財(cái)富。

我們也已經(jīng)聽過了無(wú)數(shù)用戶畫像的神奇功能和成功案例，比如亞馬遜、淘寶的機(jī)器學(xué)習(xí)團(tuán)隊(duì)使用用戶的瀏覽行為、購(gòu)物車狀態(tài)和購(gòu)買記錄開發(fā)關(guān)聯(lián)推薦系統(tǒng)，使點(diǎn)擊率和銷量大幅提升；比如應(yīng)用市場(chǎng)根據(jù)過往APP安裝記錄記對(duì)每個(gè)使用者進(jìn)行精準(zhǔn)推薦；再比如音樂，圖書和新聞網(wǎng)站通過協(xié)同過濾的方式為用戶呈現(xiàn)個(gè)性化的定制內(nèi)容。要做到這些，就必須對(duì)用戶的數(shù)據(jù)進(jìn)行關(guān)聯(lián)分析，得到精準(zhǔn)的推薦算法。

今天的格物匯，就帶大家來了解關(guān)聯(lián)分析理論和經(jīng)典的Apriori算法。

關(guān)聯(lián)分析是數(shù)據(jù)挖掘中一項(xiàng)基礎(chǔ)又重要的技術(shù)，是一種在大型數(shù)據(jù)庫(kù)中發(fā)現(xiàn)變量之間有趣關(guān)系的方法,能從數(shù)據(jù)中挖掘出潛在的關(guān)聯(lián)關(guān)系。或者說，關(guān)聯(lián)分析是發(fā)現(xiàn)交易數(shù)據(jù)庫(kù)中不同商品（項(xiàng)）之間的聯(lián)系。比如，在著名的購(gòu)物籃事務(wù)（market basket transactions）問題中，用戶在超市里購(gòu)物數(shù)據(jù)如下：

關(guān)聯(lián)分析則被用來找出此類規(guī)則：顧客在買了某種商品時(shí)也會(huì)買另一種商品。在上述例子中，有的關(guān)聯(lián)規(guī)則是很容易理解的比如：{牛奶}→{面包}，此外我們還會(huì)挖掘出另外的某些規(guī)則： {尿布} → {啤酒}；即顧客在買完尿布之后通常會(huì)買啤酒。后來通過調(diào)查分析，原來妻子囑咐丈夫給孩子買尿布時(shí)，丈夫在買完尿布后通常會(huì)買自己喜歡的啤酒。

但是，如何衡量這種關(guān)聯(lián)規(guī)則是否靠譜呢？我們需要如下指標(biāo)來衡量。

我們想找出這樣的規(guī)律需要從兩個(gè)方面考慮：這個(gè)規(guī)律中的兩個(gè)商品頻繁出現(xiàn)，兩個(gè)商品關(guān)聯(lián)出現(xiàn)的概率較大。如果兩個(gè)商品不是頻繁出現(xiàn)的，那么有可能是小眾群體的個(gè)別需求。我們把兩個(gè)商品一起出現(xiàn)的概率稱為支持度。

如果有一個(gè)商品A出現(xiàn)的非常頻繁比如90%，而另一個(gè)商品B雖然跟A一起出現(xiàn)的概率很大，但是概率大的原因是A出現(xiàn)的太頻繁了，這也不能反映出其關(guān)聯(lián)關(guān)系，我們把A出現(xiàn)B則出現(xiàn)的條件概率稱為置信度：

Apriori算法就是為了快速的找到數(shù)據(jù)中關(guān)聯(lián)的頻繁集，我們用一個(gè)具體的案例來看看吧：假設(shè)我們有4種商品：商品0，商品1，商品2和商品3。那么所有可能被一起購(gòu)買的商品組合都有哪些？這些商品組合可能只有一種商品，比如商品0，也可能包括兩種、三種或者所有四種商品。我們并不關(guān)心某人買了兩件商品0以及四件商品2的情況，我們只關(guān)心他購(gòu)買了一種或多種商品。我們可以窮舉出該顧客購(gòu)買商品所有可能的組合：

一個(gè)簡(jiǎn)單粗暴的求解方法是：我們?cè)O(shè)定支持度和置信度的閾值——min_sup,min_cof,并算出每一個(gè)可能組合的支持度和置信度，把滿足要求的組合篩選出來。如果我們的商品很多，這個(gè)方法的計(jì)算量將呈指數(shù)的增長(zhǎng)，是很難實(shí)現(xiàn)的。

定理：如果一個(gè)項(xiàng)集是頻繁的，那么其所有的子集（subsets）也一定是頻繁的。

這個(gè)定理顯而易見，假如{A,B,C}出現(xiàn)的概率大，那么{A,B}，{C},出現(xiàn)的概率肯定也很大。這看上去沒什么用，其實(shí)它的逆反定理更有用。

逆反定理：如果一個(gè)項(xiàng)集是非頻繁的，那么其所有的超集（supersets）也一定是非頻繁的。

假如{A}出現(xiàn)的概率很小，那么{A,C}，{A,B,C}出現(xiàn)的概率肯定也很小。根據(jù)這個(gè)逆反定理，我們可以排除很多不必要的計(jì)算。

比如我們發(fā)現(xiàn){2，3}是非頻繁的，那么{0，2，3}，{1，2，3}，{0，1，2，3}肯定都是非頻繁的。就可以大大減少我們計(jì)算的復(fù)雜度。

Apriori算法的目標(biāo)是找到最大的K項(xiàng)頻繁集，這里有兩層意思，首先，我們要找到符合支持度標(biāo)準(zhǔn)的頻繁集。但是這樣的頻繁集可能有很多。當(dāng)然我們可以根據(jù)上面的逆反定理減少頻繁集的計(jì)算范圍，第二層意思就是我們要找到最大個(gè)數(shù)的頻繁集。比如我們找到符合支持度的頻繁集AB和ABE，那么我們會(huì)拋棄AB，只保留ABE，因?yàn)锳B是2項(xiàng)頻繁集，而ABE是3項(xiàng)頻繁集。那么具體的，Apriori算法是如何做到挖掘K項(xiàng)頻繁集的呢？我們可以看下面這個(gè)圖：

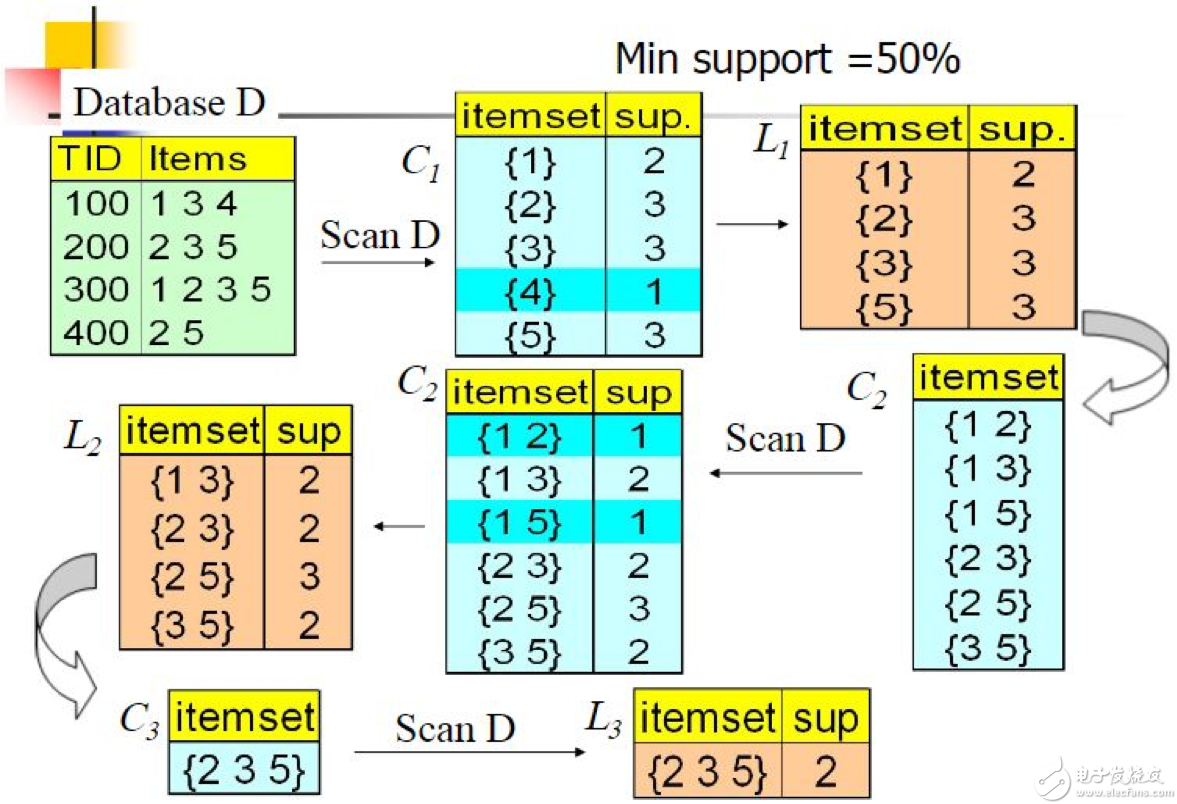
Apriori算法采用了迭代的方法，線設(shè)定支持度的閾值0.5，先搜索出候選1項(xiàng)集及對(duì)應(yīng)的支持度C1，剪枝去掉低于支持度的1項(xiàng)集，也就是圖C1中的{4}，得到頻繁1項(xiàng)集L1。然后對(duì)剩下的頻繁1項(xiàng)集進(jìn)行連接，得到候選的頻繁2項(xiàng)集，篩選去掉低于支持度的候選頻繁2項(xiàng)集C2，也就是圖中C2的{1，2}和{1，5}，得到真正的頻繁二項(xiàng)集L2，以此類推，迭代下去，直到無(wú)法找到頻繁k+1項(xiàng)集為止，對(duì)應(yīng)的頻繁k項(xiàng)集的集合即為算法的輸出結(jié)果。也就是用戶的購(gòu)物籃中，商品2，商品3，商品5常常一起購(gòu)買。

總而言之，Apriori算法是一個(gè)非常經(jīng)典的頻繁項(xiàng)集的挖掘算法，很多算法都借用了其算法的思想，并做出了改進(jìn)，我們也將在格物匯之后的文章中進(jìn)行分享。

本文作者：格創(chuàng)東智OT團(tuán)隊(duì)（轉(zhuǎn)載請(qǐng)注明作者及來源）