對于那些聽說過卻又對它們沒有特別清晰的認識的小伙伴們，這篇文章非常值得一讀。Kunlun Bai 是一位人工智能、機器學習、物體學以及工程學領域的研究型科學家，在本文中，他詳細地介紹了 2D、3D、1x1 、轉置 、空洞（擴張）、空間可分離、深度可分離、扁平化、 分組等十多種卷積網絡類型。

如果你曾聽過深度學習的各種卷積網絡（例如 2D/3D/ 1x1 / 轉置 /空洞（擴張）/ 空間可分離 / 深度可分離 /扁平化 / 分組 / 混洗分組卷積）并疑惑它們到底都是什么的話，你可以通過這篇文章了解它們實際的工作原理。

在文中，我概括性地介紹了在深度學習中常見的幾種卷積，并采用了大家都能夠明白的方式來解釋它們。針對這一主題，這篇文章以外也有其他的一些文章可供大家參考，我將這些文章的鏈接附在了文末參考部分，大家可前往閱讀。

希望這篇文章能夠幫助大家建立起對這幾種卷積的認知，并為大家的學習/研究帶來有用的參考價值。

1. 卷積 VS 互關聯

卷積是一項廣泛應用于信號處理、圖像處理以及其他工程/科學領域的技術。在深度學習中，卷積神經網絡（CNN）這一模型架構就由這項技術命名的。然而，深度學習中的卷積本質上就是信號/圖像處理中的互關聯（cross-correlation）。二者間只有細微的差別。

不深入考慮細節的話，二者的區別在于：在信號/圖像處理中，卷積被定義為：

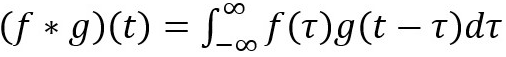
它的定義是：一個函數經過翻轉和移動后與另一個函數的乘積的積分。下面的圖像形象化地展示了這個思想：

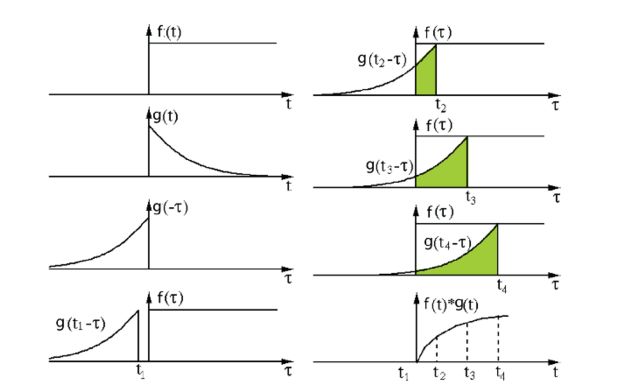
信號處理中的卷積。過濾函數 g 經過翻轉然后沿著橫軸滑動。對于該函數在橫軸上滑過的每個點的位置，都計算出函數 f 與翻轉后的函數 g 的重合區域。這個重合的區域就是函數 g 在橫軸上滑過的某個特定位置的卷積值。圖像來源：http://fourier.eng.hmc.edu/e161/lectures/convolution/index.html

在這里，函數 g 是一個過濾函數。這個函數經過翻轉然后沿著橫軸滑動。對于該函數在橫軸上滑過的每個點的位置，都計算出函數 f 與翻轉后的函數 g 的重合區域。這個重合的區域就是函數 g 在橫軸上滑過的某個特定位置的卷積值。

而另一方面，互關聯是這兩個函數的滑動的點積（dot product）或滑動的內積（inner-product）。互關聯的過濾函數不經過翻轉，它直接滑動通過函數 f。函數 f 和函數 g 的重合區域就是互關聯。下圖展示了卷積和互關聯的區別：

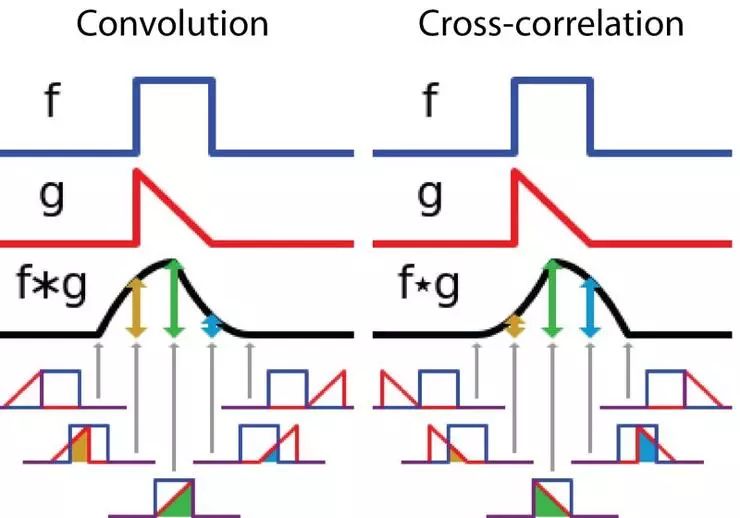
在信號處理中，卷積和互關聯的區別。圖像來源：https://en.wikipedia.org/wiki/Convolution

在深度學習中，卷積中的過濾函數是不經過翻轉的。嚴格來說，它就是互關聯。我們本質上就是在執行 element-wise 乘法和加法。但是，這個「卷積」僅在深度學習中被稱為卷積，可以這樣做的原因是因為卷積在訓練期間就學到了過濾函數的權重，如果上面示例中的經翻轉的函數 g 是正確的函數，那么經過訓練后，卷積所學到的過濾函數就會找到翻轉后的函數 g。因此，在正確的卷積中，就不需要在訓練前早早地翻轉過濾函數。

2. 深度學習中的卷積

執行卷積的目的就是從輸入中提取有用的特征。在圖像處理中，執行卷積操作有諸多不同的過濾函數可供選擇，每一種都有助于從輸入圖像中提取不同的方面或特征，如水平/垂直/對角邊等。類似地，卷積神經網絡通過卷積在訓練期間使用自動學習權重的函數來提取特征。所有這些提取出來的特征，之后會被「組合」在一起做出決策。

進行卷積操作有許多優勢，例如權重共享（weights sharing）和平移不變性（translation invariant）。此外，卷積也可以考慮到像素的空間關系。這些優勢都非常有幫助，尤其是在許多的計算機視覺任務中，因為這些任務往往涉及到對某些組成部分與其他組成部分有某些空間關系的目標進行識別（例如一只狗的身體通常是跟它的腦袋、四條腿以及尾巴相連的）。

2.1 卷積：單通道版

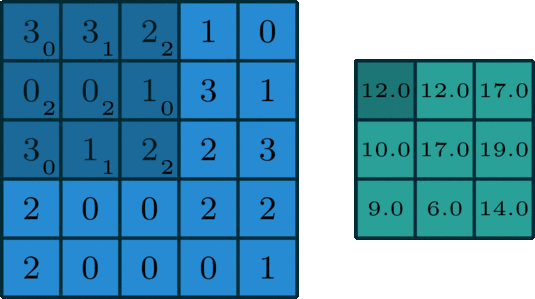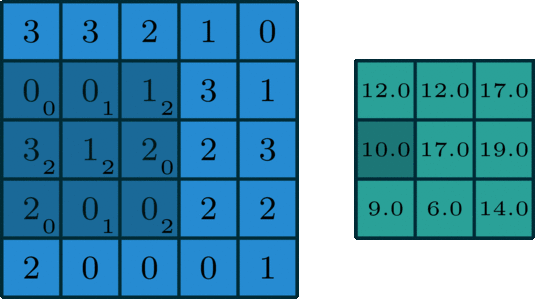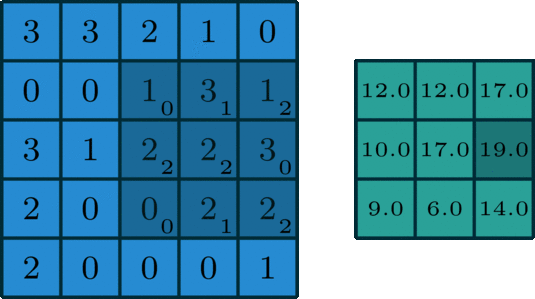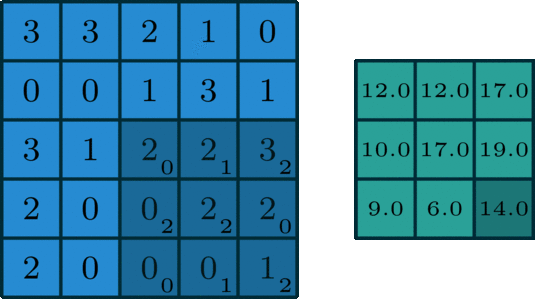
面向單通道的卷積，圖像源自：https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

在深度學習中，卷積就是元素級別（element-wise） 的乘法和加法。對于一張僅有 1 個通道的圖像，卷積過程如上圖所示，過濾函數是一個組成部分為 [[0, 1, 2], [2, 2, 0], [0, 1, 2]] 的 3 x 3 矩陣，它滑動穿過整個輸入。在每一個位置，它都執行了元素級別的乘法和加法，而每個滑過的位置都得出一個數字，最終的輸出就是一個 3 x 3 矩陣。（注意：在這個示例中，卷積步長=1；填充=0。我會在下面的算法部分介紹這些概念。）

2.2 卷積：多通道版

在許多應用中，我們處理的是多通道的圖像。一個典型的案例就是 RGB 圖像，如下圖所示，每一個 RGB 通道都分別著重于原始圖像的不同方面。

每一個 RGB 通道都分別著重于原始圖像的不同方面，圖片拍攝于：中國云南元陽

另一個多通道數據的案例就是卷積神經網絡中的層。一個卷積網絡層往往都由多個通道（一般為數百個通道）組成，每一個通道描述出前一個層的不同方面。那我們如何實現不同深度的層之間的過渡呢？又如何將深度為 n 的層轉化為后面的深度為 m 的層呢？

在介紹這個過程之前，我們先搞清楚幾個名詞：層（layer）、通道（channel）、特征映射（feature map）、過濾器（filter）以及卷積核（kernel）。從層級角度來說，「層」和「過濾器」的概念屬于一個層級，而「通道」和「卷積核」都在下一個層級。「通道」和「特征映射」是指同一個東西。一層可以有多個通道（或特征映射）；如果輸入的是 RGB 圖像，那這個輸入層有 3 個通道。「通道」一般用來形容「層」的架構。類似地，「卷積核」則用來形容「過濾器」的架構。

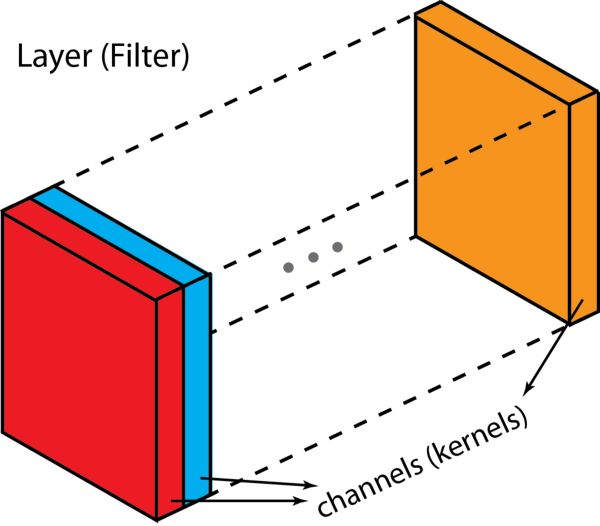
「層」（「過濾器」）和「通道」（「卷積核」）之間的區別

過濾器和卷積核之間的區別非常微妙，有時候，二者可以交替使用，這無疑就制造了些困惑。但根本上來講，二者還是有些細微區別的：「卷積核」指的是指權重組成的 2D 數組 ；「過濾器」則是由多個卷積核堆疊在一起的 3D 架構概念。對于一個 2D 過濾器來說，過濾器就相當于卷積核，但是對于一個 3D 過濾器以及深度學習中的大多數卷積而言，一個過濾器由一組卷積核組成。每個卷積核都是獨一無二的，強調了輸入通道的不同方面。

帶著對這些概念的了解，下面讓我們一起來看看多通道卷積。生成一個輸出通道，就需要將每一個卷積核應用到前一層的輸出通道上，這是一個卷積核級別的操作過程。我們對所有的卷積核都重復這個過程以生成多通道，之后，這些通道組合在一起共同形成一個單輸出通道。下圖可以讓大家更清晰地看到這個過程。

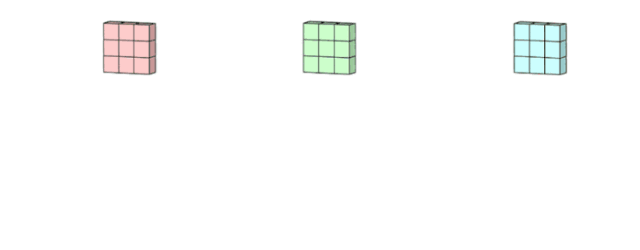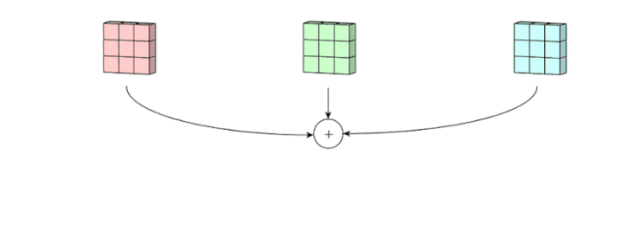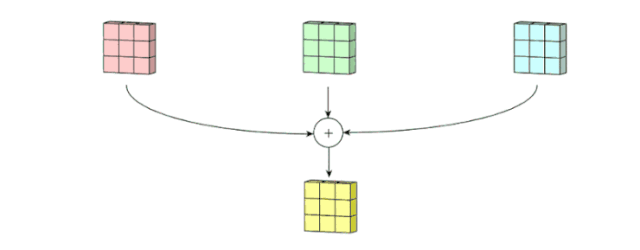
這里假設輸入層是一個 5 x 5 x 3 矩陣，它有 3 個通道。過濾器則是一個 3 x 3 x 3 矩陣。首先，過濾器中的每個卷積核都應用到輸入層的 3 個通道，執行 3 次卷積后得到了尺寸為 3 x 3 的 3 個通道。

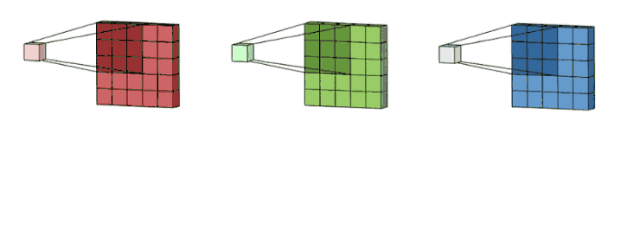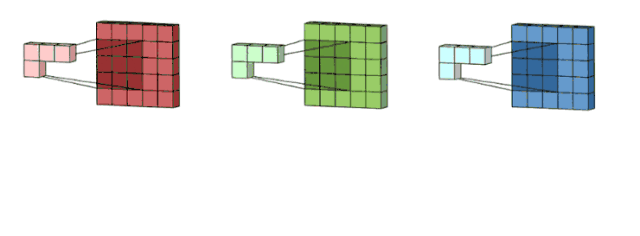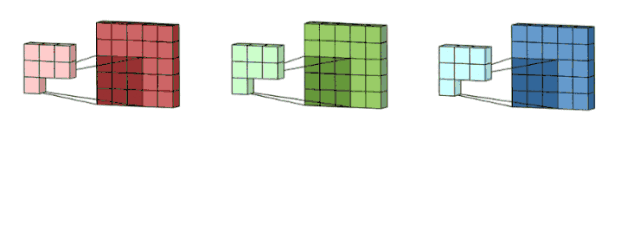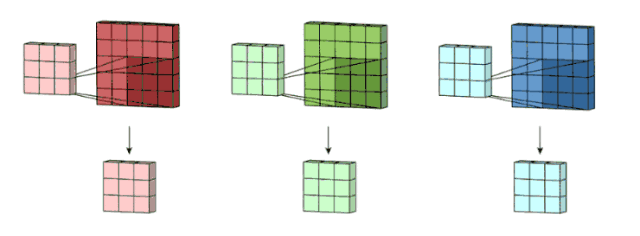
面向多通道的 2D 卷積的第一步：過濾器每個卷積核分別應用到輸入層的 3 個通道上。圖片源自：https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

之后，這 3 個通道都合并到一起（元素級別的加法）組成了一個大小為3 x 3 x 1 的單通道。這個通道是輸入層（5 x 5 x 3 矩陣）使用了過濾器（3 x 3 x 3 矩陣）后得到的結果。

面向多通道的 2D 卷積的第二步：3 個通道都合并到一起（元素級別的加法）組成了一個大小為3 x 3 x 1 的單通道。圖片源自：https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1

同樣地，我們可以將這個過程視作將一個 3D 過濾器矩陣滑動通過輸入層。注意，這個輸入層和過濾器的深度都是相同的（即通道數=卷積核數）。這個 3D 過濾器僅沿著 2 個方向（圖像的高&寬）移動（這也是為什么3D 過濾器即使通常用于處理 3D 體積數據，但這樣的操作還是被稱為 2D 卷積）。在每一個滑過的位置，我們都執行元素級別的乘法和加法，最終得出一個數值。下面這個例子中，過濾器橫向滑過 5 個位置、縱向滑過 5 個位置。全部完成后，我們得到了一個單輸出通道。

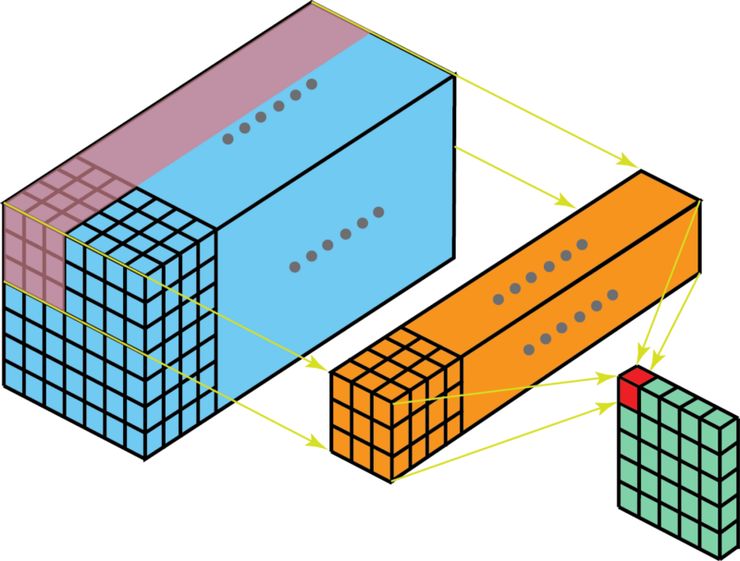
看待 2D 卷積的另一個角度：將這個過程視作將一個 3D 過濾器矩陣滑動通過輸入層。注意，這個輸入層和過濾器的深度都是相同的（即通道數=卷積核數）。這個 3D 過濾器僅沿著 2 個方向（圖像的高&寬）移動（這也是為什么3D 過濾器即使通常用于處理 3D 體積數據，但這樣的操作還是被稱為 2D 卷積）。輸出是一個 1 層的矩陣。

現在我們可以看到如何在不同深度的層之間實現過渡。假設輸入層有 Din 個通道，而想讓輸出層的通道數量變成Dout，我們需要做的僅僅是將 Dout 個過濾器應用到輸入層中。每一個過濾器都有 Din 個卷積核，都提供一個輸出通道。在應用 Dout 個過濾器后，Dout 個通道可以共同組成一個輸出層。

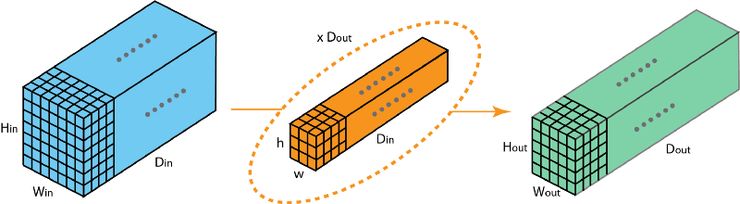
標準 2D 卷積。通過使用 Dout 個過濾器，將深度為 Din 的層映射為另一個深度為 Dout 的層。

3.3D 卷積

在上部分的最后一張圖中，我們看到了將卷積在 3D 體積上的執行情況。但是一般而言，我們依舊將這一操作視為深度學習中的 2D 卷積——3D 體積數據上的 2D 卷積：其過濾器和輸入層的深度是一樣的；3D 過濾器僅沿著 2 個方向（圖像的高&寬）移動。這樣操作得出的結果就是一個 2D 圖像（僅有 1 個通道）。

有 2D 卷積，自然就有 3D 卷積。3D 卷積是 2D 卷積的一般化。在 3D 卷積中，過濾器的深度要比輸入層的深度更小（卷積核大小<通道大小），結果是，3D 過濾器可以沿著所有 3 個方向移動（高、寬以及圖像的通道）。每個位置經過元素級別的乘法和算法都得出一個數值。由于過濾器滑動通過 3D 空間，輸出的數值同樣也以 3D 空間的形式呈現，最終輸出一個 3D 數據。

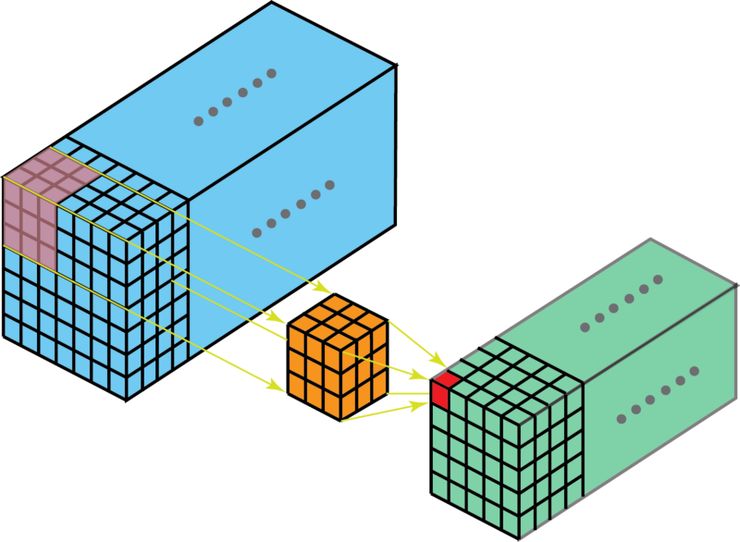
在 3D 卷積中，過濾器的深度要比輸入層的深度更小（卷積核大小<通道大小），結果是，3D 過濾器可以沿著所有 3 個方向移動（高、寬以及圖像的通道）。每個位置經過元素級別的乘法和算法都得出一個數值。由于過濾器滑動通過 3D 空間，輸出的數值同樣也以 3D 空間的形式呈現，最終輸出一個 3D 數據。

和對 2D 區域中目標的空間關系進行解碼的 2D 卷積相似，3D 卷積也可以描述 3D 空間中目標的空間關系。對于一些應用來說，這種 3D 關系很重要，例如在 CT 和 MRI 等生物醫學圖像的 3D 分割/重建中，這些圖像的目標如血管都是蜿蜒分布在 3D 空間中的。

4. 1x1 卷積

由于我們在前一個部分——3D 卷積中探討了深度級別的操作，接下來讓我們了解另一個有趣的操作，1 x 1 卷積。

你或許想知道為什么這個卷積是有幫助作用的。我們剛剛是否讓輸入層中的每個數值都乘以了一個數值？是，也不是。對于僅有 1 個通道的層來說，這項操作不重要。在上面的示例中，我們讓每一個組成部分都乘以了一個數值。

如果輸入層有多個通道，那事情就變得非常有趣了。下圖闡述了 1 x 1 卷積在一個維度為 H x W x D 的輸入層上的操作方式。經過大小為 1 x 1 x D 的過濾器的 1 x 1 卷積，輸出通道的維度為 H x W x 1。如果我們執行 N 次這樣的 1 x 1 卷積，然后將這些結果結合起來，我們能得到一個維度為 H x W x N 的輸出層。

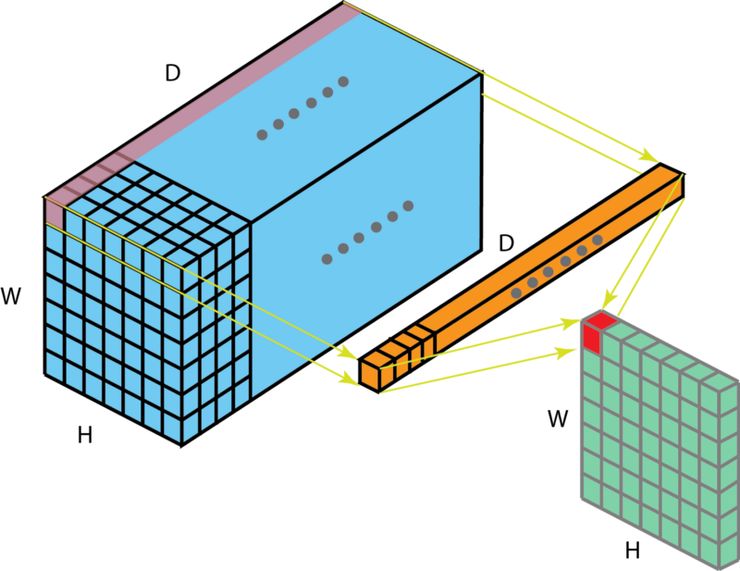
過濾器大小為 1 x 1 x D 的1 x 1 卷積

1 x 1 卷積最初是在 Network-in-network 的論文（論文閱讀地址：https://arxiv.org/abs/1312.4400）中被提出的，之后在谷歌的 Inception 論文（論文閱讀地址：https://arxiv.org/abs/1409.4842）中被大量使用。

1 x 1 卷積具有如下幾個優勢：

減少維度以實現更有效率的計算；

進行更有效率的低維度嵌入，或者對特征進行池化；

卷積以后反復應用非線性特征。

前兩個優勢我們可以從上面的圖像中觀察到。執行 1 x 1 卷積后，我們明顯減少了維度的深度級別。假設原始輸入有 200 個通道，1 x 1 卷積會將這些通道（特征）嵌入到一個單通道中。第三個優勢在 1 x 1 卷積執行后才顯現出來，它會將線性整流函數（ReLU）等非線性激活函數添加進模型中。非線性特征讓網絡學習更復雜的函數。

谷歌的 Inception 論文中也對這些優勢進行了描述：

上面這個模塊（至少在這個樸素的形式中）的一個大問題是，即便是數量適度的 5 x 5 卷積，在有大量過濾器的卷積層之上的計算也會過于昂貴。

這就給提出的框架帶來了第二個思路：明智地減少維度并進行投影，不然就會過度增加對于計算的要求。這是基于成功實現嵌入上的：即便是低維度的嵌入也可以容納大量關于相對較大的圖像塊的信息... 也就是說，在執行計算昂貴的 3 x 3 卷積和 5 x 5 卷積前，往往會使用 1 x 1 卷積來減少計算量。此外，它們也可以利用調整后的線性激活函數來實現雙重用途。

針對 1 x 1 卷積，Yann LeCun 提出了一個非常有趣的角度：「在卷積網絡中，不存在像「全連接層」這樣的東西，而只有含有一些 1x1 卷積核和 1 個全連接表的卷積層」

5. 卷積算法

我們現在知道了如何處理卷積的深度。接下來討論一下怎樣處理在其他兩個方向（高&寬）中的卷積，以及重要的卷積算法（convolution arithmetic）。

這里有一些需要了解的名詞：

卷積核大小（Kernel size）：卷積核在前一部分已經討論過了。卷積核大小確定卷積的視野。

卷積步長（Stride）：它確定的是卷積核滑動通過圖像的步長。步長為 1 表示卷積核一個像素一個像素地滑動通過圖像；步長為 2 則表示卷積核在圖像上每滑動一次就移動了 2 個像素（即跳過 1 個像素）。對于下面這個案例中的圖像，我們采用大于或等于 2 的步長。

填充（Padding）：填充定義如何處理圖像的邊界。如果有必要的話，可以通過將輸入邊界周圍的填充設置為 0，這樣的話，經過填充后的卷積（Tensorflow 中的「相同」填充）就可以保持空間輸出維度與輸入圖像的維度一樣。另一方面，如果不在輸入邊界周圍添加 0 填充，未填充的卷積（Tensorflow 中的「有效」填充）僅對輸入圖像的像素執行卷積，輸出大小也會小于輸入大小。

下圖表示使用卷積核大小為 3、步長為 1；填充為 1 的 2D 卷積：

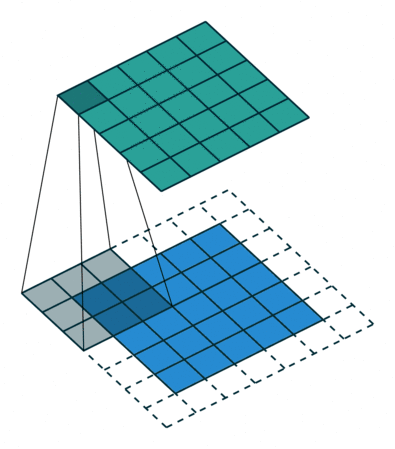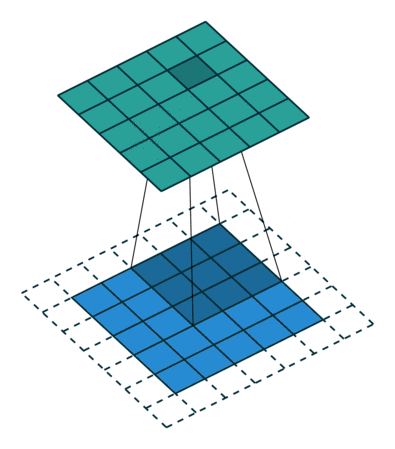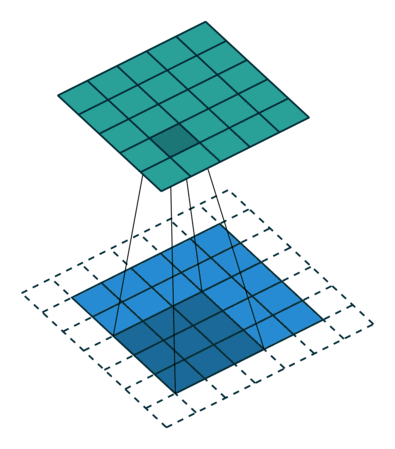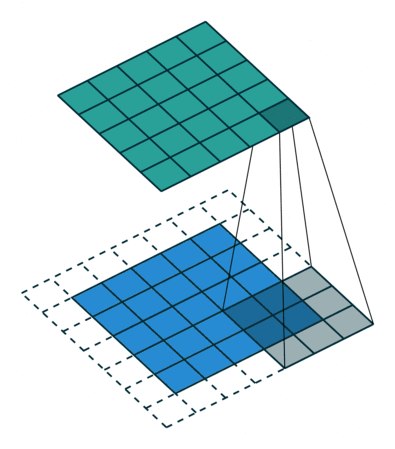
這里有一篇不錯的文章（A guide to convolution arithmetic for deep learning，https://arxiv.org/abs/1603.07285）詳細地描述了算法，大家可前往閱讀。這篇文章對其進行了詳細介紹，并針對不同的卷積核大小、卷積步長以及填充分別進行了案例分析。這里我僅僅概括出了最常用的結果：

對于一個大小為 i、卷積核大小為 k、填充為 p 以及卷積步長為 s 的輸入圖像，經過卷積的輸出圖像的大小為 o：

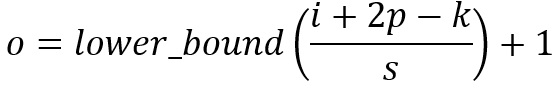
6. 轉置卷積（反卷積）

對于許多應用以及在許多網絡架構中，我們通常需要朝與標準卷積相反的方向做轉換，例如，當我們想要執行上采樣（up-sampling）時。這些案例其中就包括生成高分辨率圖像以及在自動編碼器或語義分割中將低維度特征映射映射到高維度空間中。（在隨后的案例中，語義分割首先在編碼器中提取特征映射，然后在解碼器中還原原始圖像的大小從而能夠在原始圖像中對每一個像素進行分類。）

傳統上，研究者可以通過應用插值（interpolation）方案或者手動創建規則來實現上采樣。神經網絡等現代架構則反過來趨向于讓網絡自己自動學習合適的轉換，而不需要人類的干預。我們可以使用轉置卷積（Transposed Convolution）來實現這一點。

在書面表達上，轉置卷積也稱作反卷積（deconvolution），或小數步長的卷積（fractionally strided convolution）。不過值得一提的是，將其稱作「反卷積」并不是那么合適，因為轉置卷積并不完全是信號/圖像處理中所定義的反卷積。從技術上來說，信號處理中的反卷積是卷積的逆向操作，跟這里所說的轉置卷積不一樣。正因為此，一些論文作者強烈反對將轉置卷積稱作反卷積，而大眾要這樣稱呼主要是為了簡單起見。隨后，我們會探討為什么將這種操作稱作轉置卷積才是自然且更合適的。

我們可以直接使用卷積來實現轉置卷積。例如在下圖的案例中，我們 2 x 2 的輸入上做轉置卷積：其卷積核為 3 x 3，卷積步長為 1，填充為 2 x 2 的空格。上采樣的輸出大小為 4 x 4。

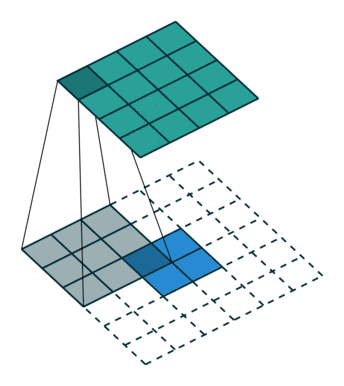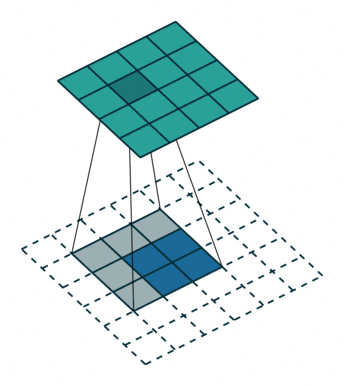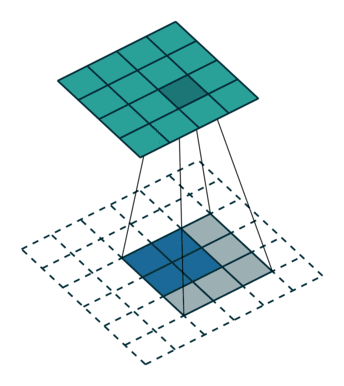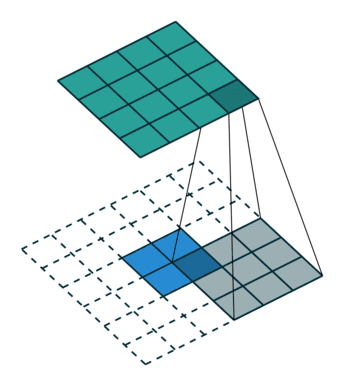
將2x 2 輸入上采樣為4x 4 輸出，圖片源自：https://github.com/vdumoulin/conv_arithmetic

非常有趣的是，研究者可以通過應用花式填充和步長，將相同的 2 x 2 輸入圖像映射出不同的圖像大小。下圖中，在同一個卷積核為 3 x 3，卷積步長為 1，填充為 2 x 2 空格的 2 x 2 的輸入（輸入之間插入了一個空格）上做轉置卷積，得出的輸出大小為 5 x 5。

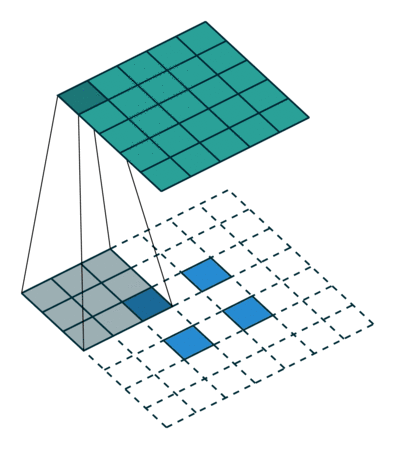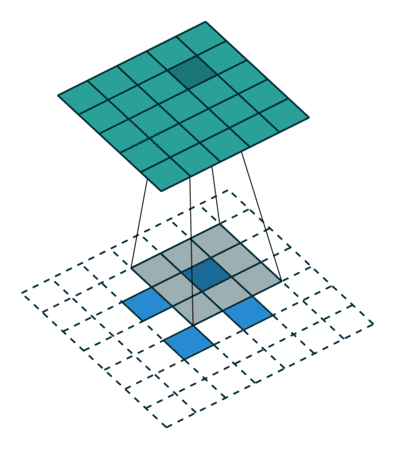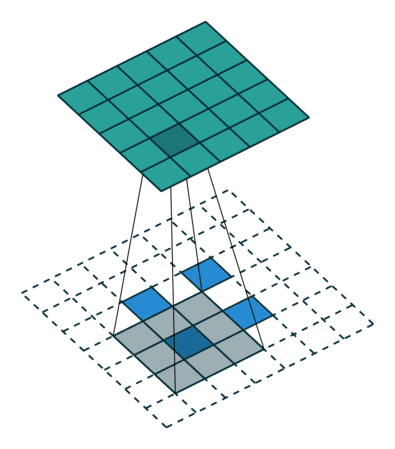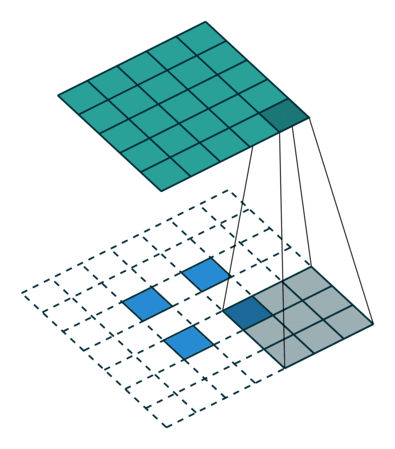
將2x 2 輸入上采樣為5x 5 輸出，圖片源自：https://github.com/vdumoulin/conv_arithmetic

通過觀察上述案例中的轉置卷積，我們可以初步建立一些認知。但是要想較好地掌握它的應用，在電腦上看看它怎樣通過矩陣乘法來實現會比較有用。從中，我們還可以了解到為什么「轉置卷積」這個名字更合適。

在卷積中，我們設定卷積核為 C，輸入圖像為 Large，卷積輸出的圖像為 Small。在做卷積（矩陣乘法）后，我們將大圖像下采樣（down-sample）為小的輸出圖像。矩陣乘法中的卷積實現遵循 C x Large = Small。

下面案例顯示了這項操作如何實現。它將輸入也壓平為 16 x 1 矩陣，之后將卷積核轉換為一個稀疏矩陣 (4 x 16)，接著在稀疏矩陣和壓平的輸入間執行矩陣乘法運算，最終得出的矩陣（4 x 1）轉換回 2 x 2 的輸出。

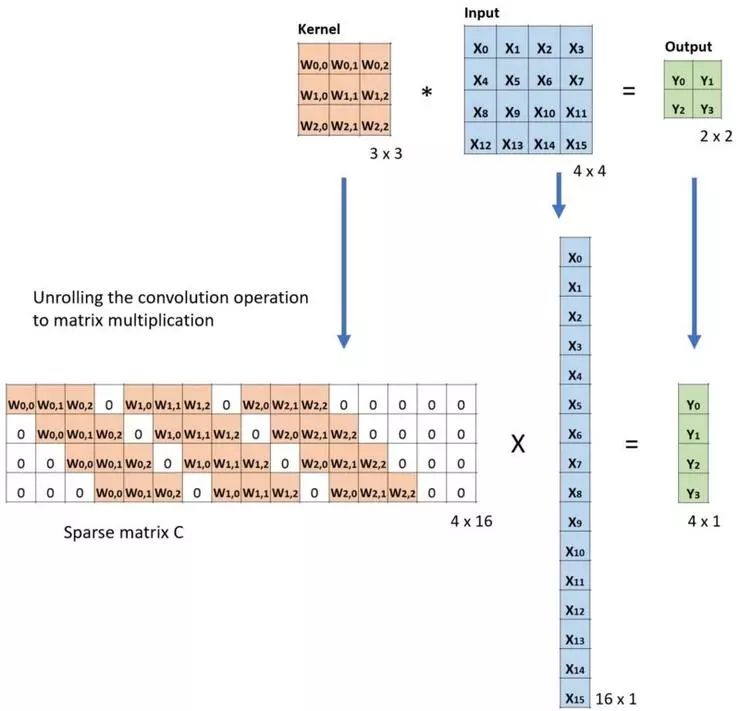
卷積的矩陣乘法：從大小4 x 4為Large 輸入圖像到大小為2 x 2 的 Small 輸出圖像

現在，如下圖所示，如果我們對等式兩邊的矩陣 CT 進行多次轉置，并利用一個矩陣和其轉置矩陣相乘得出一個單元矩陣的屬性，我們可以得出下面的運算公式：CT x Small = Large。

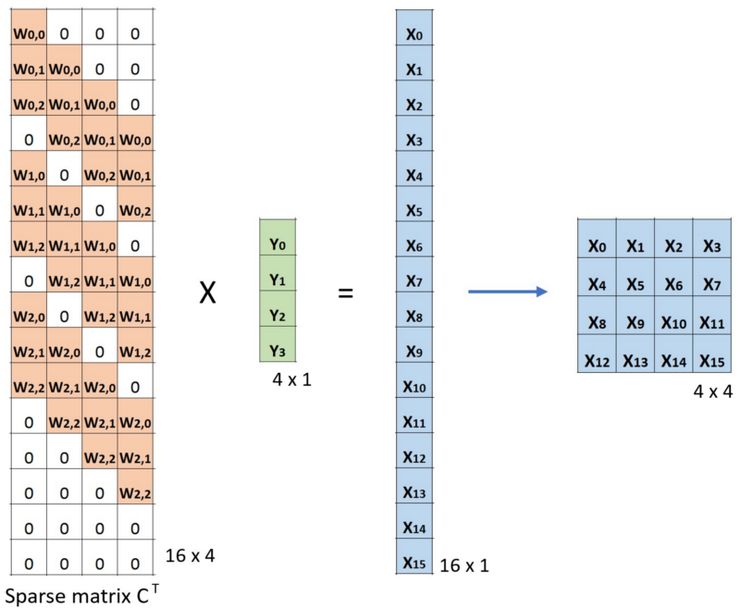
卷積的矩陣乘法：從大小2x 2為Large 輸入圖像到大小為4 x 4 的 Small 輸出圖像

正如你在這里看到的，轉置卷積執行的是從小圖像到大圖像的上采樣。這也是我們所要實現的。而現在，你也可以了解到「轉置卷積」這個名字的由來。

轉置卷積的通用算法可以在《深度學習的卷積算法指南》「A guide to convolution arithmetic for deep learning」這篇文章的「Relationship 13」和「Relationship 14」章節中找到。

6.1 棋盤效應

所謂的「棋盤效應」（Checkerboard artifacts），是研究人員在使用轉置卷積時可以觀察到的一種令人不快的現象（奇怪的棋盤格狀偽影）。

「棋盤效應」的一些案例。圖片源自論文「Deconvolution and Checkerboard Artifacts」，https://distill.pub/2016/deconv-checkerboard/

《反卷積和棋盤效應》（Deconvolution and Checkerboard Artifacts，https://distill.pub/2016/deconv-checkerboard）對于這一現象有一個非常好的闡述。大家可以前往閱讀這篇文章了解詳細內容。這里我僅僅概括出關鍵點。

造成棋盤效應的原因是轉置卷積的「不均勻重疊」（uneven overlap）。這種重疊會造成圖像中某個部位的顏色比其他部位更深。

在下圖中，頂部這層是輸入層，底部這層則是操作轉置卷積后的輸出層。在轉置卷積過程中，小的這層映射到大的那層。

在案例（a）中，其卷積步長為 1，過濾器大小為 2。正紅線所標出的，輸入圖像上的第一個像素映射為輸出圖像上的第一個和第二個像素。綠線標出的則是輸入圖像上的第二個像素映射為輸出圖像上的第二個和第三個像素。這樣的話，輸出圖像上的第二個像素就收到了輸入圖像上的第一個和第二個像素的雙重信息，而整個卷積過程中，輸出圖像中間部分的像素都從輸入圖像中接收到了同樣多的信息，這樣就導致了卷積核重疊的區域。而在案例（b）中，當過濾器的大小增加到 3 時，這個接收到最多信息的中間部分縮小了。但是這樣的話問題不大，因為重疊部分依舊是均勻的。在輸出圖像中間部分的像素從輸入圖像中接收到同樣多的信息。

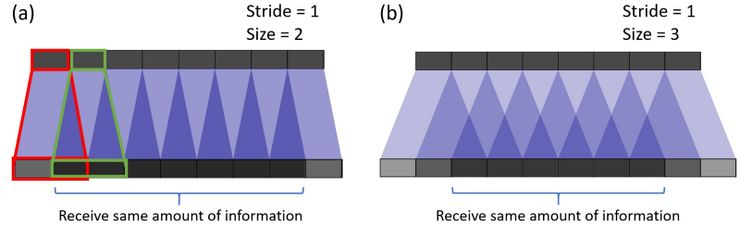
圖片源自論文「Deconvolution and Checkerboard Artifacts」，https://distill.pub/2016/deconv-checkerboard/

現在針對下面的案例，我們將卷積步長改為 2。在案例（a）中，過濾器的大小為 2，輸出圖像上的所有像素從輸入圖像中接收到同樣多的信息，它們都從輸入圖像中接收到一個像素的信息，這里就不存在轉置卷帶來的重疊區域。

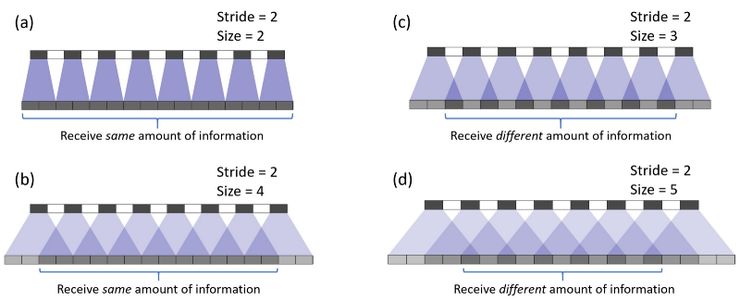
圖片源自論文「Deconvolution and Checkerboard Artifacts」，https://distill.pub/2016/deconv-checkerboard/

而在案例（b）中，當我們將過濾器大小增至 4 時，均勻的重疊區域縮小了，但是研究者依舊可以將輸出圖像的中間部分用作有效的輸出，其中每個像素從輸入圖像中接收到的信息是同樣多的。

然而，在案例（c）和（d）中，當過濾器大小變成 3 或 5 時，情況就變得非常有趣了。在這兩個案例中，輸出圖像上的每個像素與其毗鄰的像素所接收到的信息量都不相同。研究者在輸出圖像上無法找到一個連續并均勻的重疊區域。

當過濾器大小無法被卷積步長整除時，轉置卷積就會出現「不均勻重疊」。這種「不均勻重疊」會造成圖像中某個部位的顏色比其他部位更深，因而會帶來「棋盤效應」。實際上，不均勻重疊區域會在二維上更加極端。因為二維上的兩個模式會相乘，因而最終的不均勻性是原來的平方。

在應用轉置卷積時，可以做兩件事情來減輕這種效應。第一，確認使用的過濾器的大小是能夠被卷積步長整除的，從而來避免重疊問題。第二，可以采用卷積步長為 1 的轉置卷積，來減輕「棋盤效應」。然而，正如在最近許多模型中所看到的，這種效益依舊可能會顯露出來。

這篇論文進一步提出了一個更好的上采樣方法：首先調整圖像大小（使用最近鄰域內插法（Nearest Neighbor interpolation）和雙向性內插法（bilinear interpolation）），然后制作一個卷積層。通過這樣做，論文作者成功避免了這一

「棋盤效應」。大家或許也想要在自己的應用中嘗試一下這個方法吧。

7. 空洞卷積（擴張卷積）

下面這兩篇論文對空洞卷積（Dilated Convolution）進行了介紹：

《使用深度卷積網絡和全連接 CRF 做語義圖像分割》（Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs，https://arxiv.org/abs/1412.7062）

《通過空洞卷積做多規模的上下文聚合》（Multi-scale context aggregation by dilated convolutions，https://arxiv.org/abs/1511.07122）

空洞卷積也稱作擴張卷積（Atrous Convolution）。

這是一個標準的離散卷積：

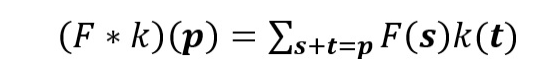
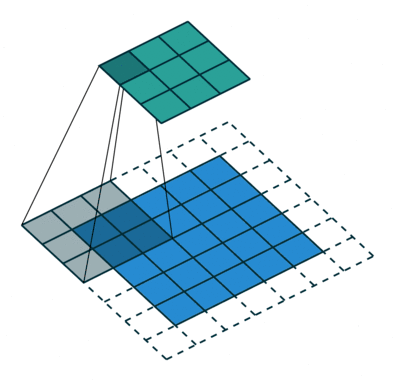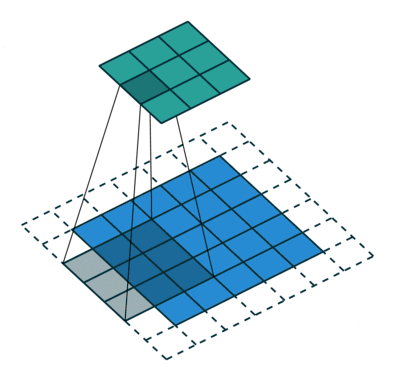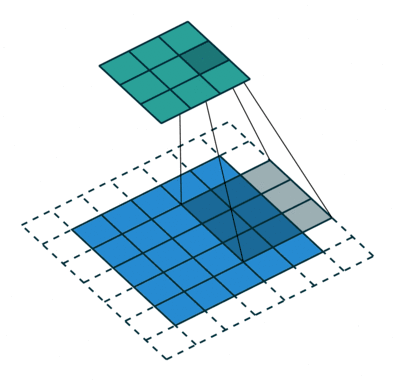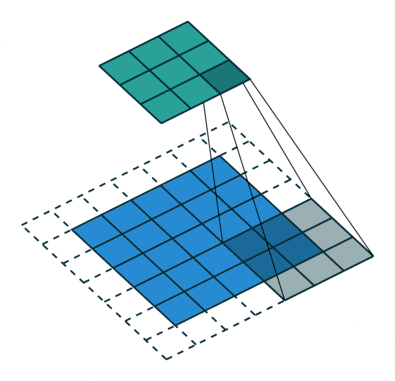
標準卷積

空洞卷積如下：

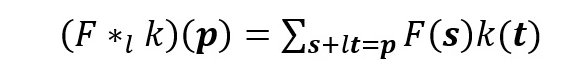
當 l=1 時，空洞卷積就變成了一個標準卷積。

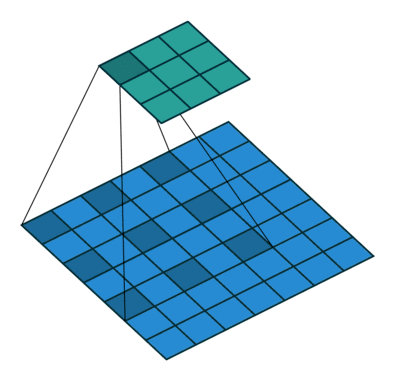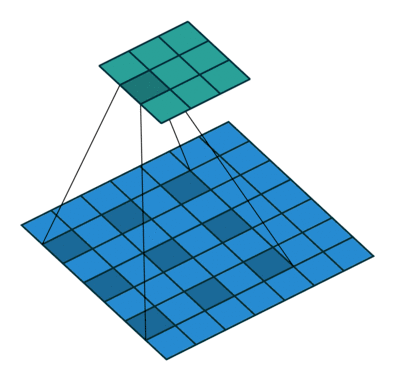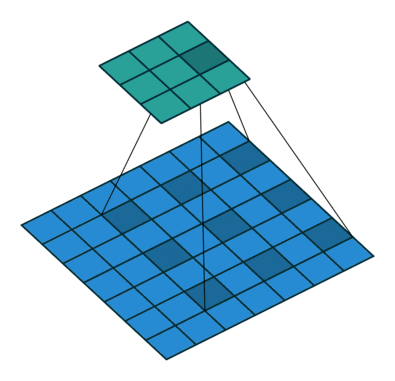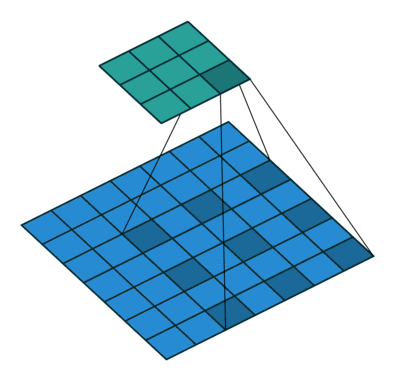
直觀上，空洞卷積通過在卷積核部分之間插入空間讓卷積核「膨脹」。這個增加的參數 l（空洞率）表明了我們想要將卷積核放寬到多大。雖然各實現是不同的，但是在卷積核部分通常插入 l-1 空間。下圖顯示了當 l-1,2,4 時的卷積核大小。

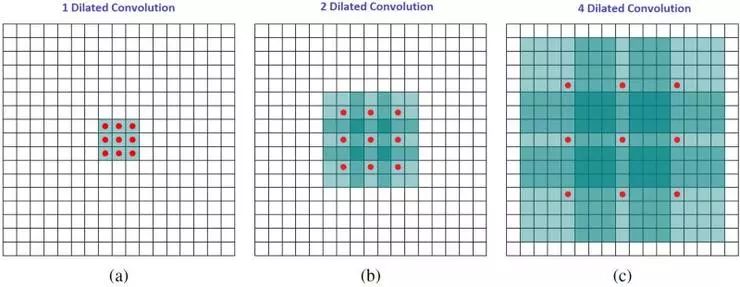
空洞卷積的感受野。本質上是在不增加額外的計算成本的情況下觀察感受野。

在圖像中，3 x 3 的紅點表明經過卷積后的輸出圖像的像素是 3 x 3。雖然三次空洞卷積都得出了相同維度的輸出圖像，但是模型觀察到的感受野（receptive field）是大不相同的。l=1 時，感受野為 3 x 3；l=2 時，感受野是 7 x 7；l=3 時，感受野增至 15x15。有趣的是，伴隨這些操作的參數數量本質上是相同的，不需要增加參數運算成本就能「觀察」大的感受野。正因為此，空洞卷積常被用以低成本地增加輸出單元上的感受野，同時還不需要增加卷積核大小，當多個空洞卷積一個接一個堆疊在一起時，這種方式是非常有效的。

《通過空洞卷積做多規模的上下文聚合》的論文作者在多層空洞卷積以外創建了一個網絡，其中的空洞率 l 每層都以指數級的方式增長。結果，當參數數量每層僅有直線式的增長時，有效的感受野實現了指數型的增長。

該論文中，空洞卷積被用于系統地聚合多規模的上下文信息，而不需要損失分辨率。該論文表明，其提出的模塊提高了當時（2016 年）最先進的語義分割系統的準確率。大家可以閱讀這篇論文獲得更多信息。

8. 可分離卷積

可分離卷積用于一些神經網絡架構，例如 MobileNet（該架構論文地址：https://arxiv.org/abs/1704.04861）。可分離卷積分為空間可分離卷積（spatially separable convolution）和深度可分離卷積（depthwise separable convolution）。

8.1 空間可分離卷積

空間可分離卷積在圖像的 2D 空間維度上執行，例如高和寬兩個維度。從概念上來看，顧名思義，空間可分離卷積將卷積分解為兩項單獨的操作。下面所展示的案例中，一個卷積核為 3x3 的 Sobel 卷積核拆分成了一個 3x1 卷積核和一個 1x3 卷積核。

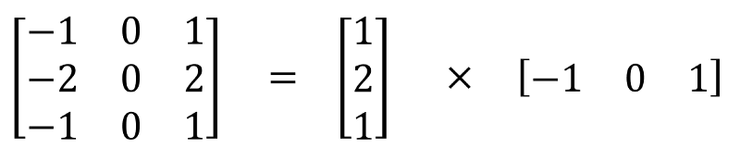
一個卷積核為 3x3 的 Sobel 卷積核拆分成了一個 3x1 卷積核和一個 1x3 卷積核

在卷積中，3x3 卷積核可以直接對圖像進行卷積操作。在空間可分離卷積中，首先由 3x1 卷積核對圖像進行卷積，之后再應用 1x3 卷積核。在執行相同的操作中，這就要求 6 個而不是 9 個參數了。

此外，比起卷積，空間可分離卷積要執行的矩陣乘法運算也更少。舉一個具體的案例，在卷積核為 3x3 的 5x5 圖像上做卷積，要求橫向掃描 3 個位置（以及縱向掃描3 個位置）上的卷積核，共有 9 個位置，如下圖標出的 9 個點所示。在每個位置都進行 9 次元素級別的乘法運算，共執行 9 x 9 = 81 次運算。

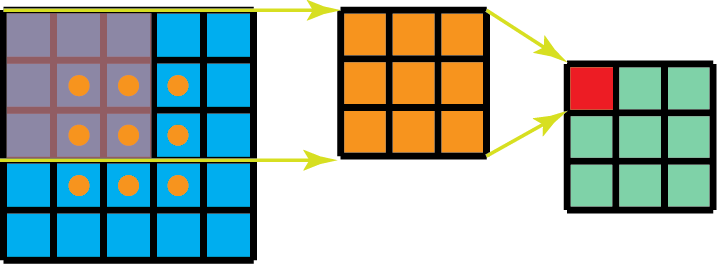
針對空間可分離卷積，另一方面，我們先在 5x5 圖像上應用一個 3x1 的過濾器，這樣的話就能橫向掃描 5 個位置的卷積核以及縱向掃描 3 個位置的卷積核，總共 5 x 3=15 個位置，如下圖所標的點所示。這樣的話就共要進行 15 x 3 = 45 次乘法運算。現在得到的是一個 3 x 5 的矩陣，這個矩陣經過 1 x 3 卷積核的卷積操作——從橫向上的 3 個位置以及縱向上的 5 個位置來掃描該矩陣。對于這 9 個位置中的每一個，都進行了 3 次元素級別的乘法運算，這個步驟總共要求 9 x 3=27 次乘法運算。因此，總體上，該空間可分離卷積共進行了 45 + 27 = 72 次乘法運算，也比標準的卷積所要進行的乘法運算次數要少。

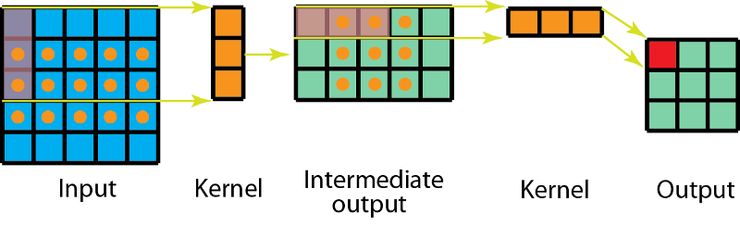
有 1 個通道的空間可分離卷積

讓我們稍微概括一下上面的案例。假設我們現在在 m x m 卷積核、卷積步長=1 、填充=0 的 N x N 圖像上做卷積。傳統的卷積需要進行 (N-2) x (N-2) x m x m 次乘法運算，而空間可分離卷積只需要進行 N x (N-2) x m + (N-2) x (N-2) x m = (2N-2) x (N-2) x m 次乘法運算。空間可分離卷積與標準的卷積的計算成本之比為：

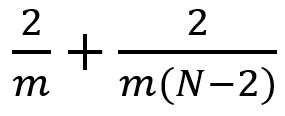
對于圖像大小 N 大于過濾器大小（N >> m），這個比率就變成了 2 / m，這就意味著在這種漸進情況（N >> m）下，對于一個 3x3 的過濾器，空間可分離卷積與標準的卷積之間的計算成本比率為 2/3；對于一個 5x5 的過濾器，比率為 2/5；對于一個 7x7 的過濾器，比如為 2/7，以此類推。

雖然空間可分離卷積節省了計算成本，但是它很少應用于深度學習中。一個主要的原因是，并不是所有的卷積核都能被拆分為 2 個更小的卷積核。如果我們用這種空間可分離卷積來取代所有傳統的卷積，就會束縛我們去搜尋訓練期間所有可能存在的卷積核，因為這個訓練結果可能是還只是次優的。

8.2 深度可分離卷積

現在，讓我們移步到深度可分離卷積，它在深度學習中的應用要更普遍得多（例如在 MobileNet 和 Xception 中）。深度可分離卷積由兩步組成：深度卷積以及 1x1 卷積。

在介紹這些步驟前，值得回顧一下前面部分所提到的 2D 卷積核 1x1 卷積。讓我們先快速過一下標準的 2D 卷積。舉一個具體的案例，假設輸入層的大小為 7 x 7 x 3（高 x 寬 x 通道），過濾器大小為 3 x 3 x 3，經過一個過濾器的 2D 卷積后，輸出層的大小為 5 x 5 x 1（僅有 1 個通道）。

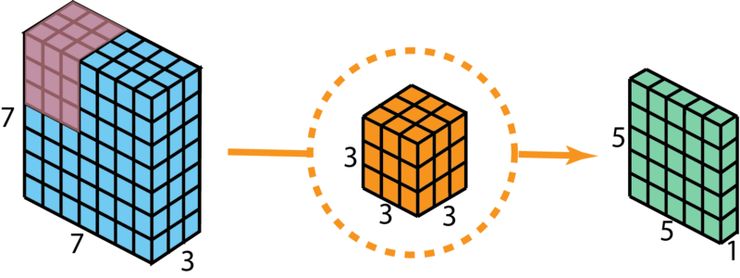
使用 1 個過濾器做標準的 2D 卷積來創建一個 1 層的輸出

一般來說，兩個神經網絡層間應用了多個過濾器，現在假設過濾器個數為 128。128 次 2D 卷積得到了 128 個 5 x 5 x 1 的輸出映射。然后將這些映射堆疊為一個大小為 5 x 5 x 128 的單個層。空間維度如高和寬縮小了，而深度則擴大了。

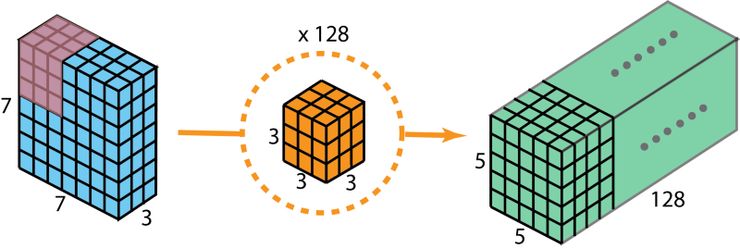
使用 128 個過濾器做標準的 2D 卷積來創建一個 128 層的輸出

接下來看看使用深度可分離卷積如何實現同樣的轉換。

首先，我們在輸入層上應用深度卷積。我們在 2D 卷積中分別使用 3 個卷積核（每個過濾器的大小為 3 x 3 x 1），而不使用大小為 3 x 3 x 3 的單個過濾器。每個卷積核僅對輸入層的 1 個通道做卷積，這樣的卷積每次都得出大小為 5 x 5 x 1 的映射，之后再將這些映射堆疊在一起創建一個 5 x 5 x 3 的圖像，最終得出一個大小為 5 x 5 x 3 的輸出圖像。這樣的話，圖像的空間維度縮小了嗎，但是深度保持與原來的一樣。

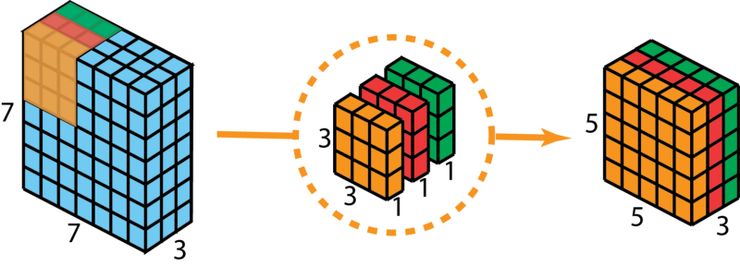
深度可分離卷積—第一步：在 2D 卷積中分別使用 3 個卷積核（每個過濾器的大小為 3 x 3 x 1），而不使用大小為 3 x 3 x 3 的單個過濾器。每個卷積核僅對輸入層的 1 個通道做卷積，這樣的卷積每次都得出大小為 5 x 5 x 1 的映射，之后再將這些映射堆疊在一起創建一個 5 x 5 x 3 的圖像，最終得出一個大小為 5 x 5 x 3 的輸出圖像。

深度可分離卷積的第二步是擴大深度，我們用大小為 1x1x3 的卷積核做 1x1 卷積。每個 1x1x3 卷積核對 5 x 5 x 3 輸入圖像做卷積后都得出一個大小為 5 x 5 x1 的映射。

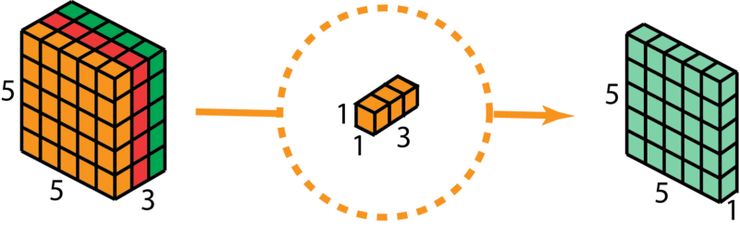
這樣的話，做 128 次 1x1 卷積后，就可以得出一個大小為 5 x 5 x 128 的層。

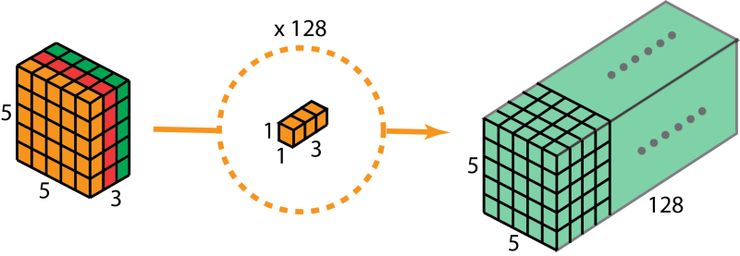
深度可分離卷積完成這兩步后，同樣可以將一個 7 x 7 x 3 的輸入層轉換為 5 x 5 x 128 的輸出層。

深度可分離卷積的完整過程如下圖所示：

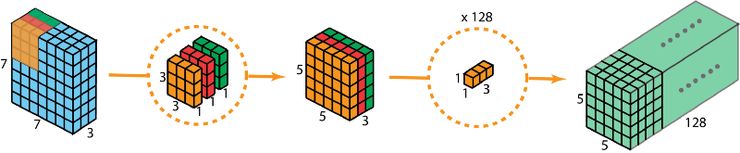
深度可分離卷積的完整過程

因此，做深度可分離卷積的優勢是什么？高效！相比于 2D 卷積，深度可分離卷積的執行次數要少得多。

讓我們回憶一下 2D 卷積案例中的計算成本：128 個 3x3x3 的卷積核移動 5x5 次，總共需要進行的乘法運算總數為 128 x 3 x 3 x 3 x 5 x 5 = 86,400 次。

那可分離卷積呢？在深度卷積這一步，有 3 個 3x3x3 的卷積核移動 5x5 次，總共需要進行的乘法運算次數為 3x3x3x1x5x5 = 675 次；在第二步的 1x1 卷積中，有 128 個 3x3x3 的卷積核移動 5x5 次，總共需要進行的乘法運算次數為 128 x 1 x 1 x 3 x 5 x 5 = 9,600 次。因此，深度可分離卷積共需要進行的乘法運算總數為 675 + 9600 = 10,275 次，花費的計算成本僅為 2D 卷積的 12%。

因此對于任意大小的圖像來說，應用深度可分離卷積能節省多少次計算呢？我們稍微概括一下上面的案例。假設輸入圖像大小為 H x W x D，2D 卷積的卷積步長為 1，填充為 0，卷積核大小為 h x h x D（兩個 h 相等）、個數為 Nc。2D 卷積后，大小為 H x W x D 的輸入層最終轉換為大小為（H-h+1）x（W-h+1）x Nc 的輸出層，總共需要進行的乘法運算次數為：Nc x h x h x D x (H-h+1) x (W-h+1)。

針對同樣的轉換，深度可分離卷積總共需要進行的乘法運算次數為：D x h x h x 1 x (H-h+1) x (W-h+1) + Nc x 1 x 1 x D x (H-h+1) x (W-h+1) = (h x h + Nc) x D x (H-h+1) x (W-h+1)。

深度可分離卷積與 2D 卷積之間的乘法運算次數之比為：

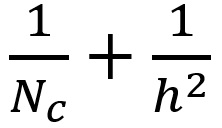
對于大部分現代框架而言，輸出層往往都有許多個通道，例如幾百甚至幾千個通道。對于 Nc >> h 的層，上面的表達式會縮短為 1/h/h，這就意味著對于這個漸進的表達式而言，如果使用的過濾器大小為 3 x 3，2D 卷積需要進行的乘法運算次數比深度可分離卷積多出 9 次；使用大小為 5 x5 的過濾器，則要多出 25 次。

使用深度可分離卷積有什么缺點嗎？當然有。深度可分離卷積會減少卷積中的參數個數，這樣的話，對于一個小的模型，如果采用深度可分離模型來踢打 2D 模型，該模型的能力就會被大為削弱。結果，該模型也會變成次優的模型。然而，如果恰當使用，深度可分離卷積可以提高效率而不會明顯損害模型的性能。

9. 扁平化卷積

《將扁平化卷積神經網絡應用于前饋加速》（Flattened convolutional neural networks for feedforward acceleration，https://arxiv.org/abs/1412.5474）這篇論文對扁平化卷積（Flattened convolutions）進行了介紹。直觀上，這種卷積的思路就是應用過濾器分離，即將標準的分離器拆分為 3 個 1D 分離器，而不是直接應用一個標準的卷積過濾器來將輸入層映射為輸出層。這個思路類似于前部分所提到的空間可分離卷積，其中的一個空間過濾器近似于兩個 rank-1 過濾器。

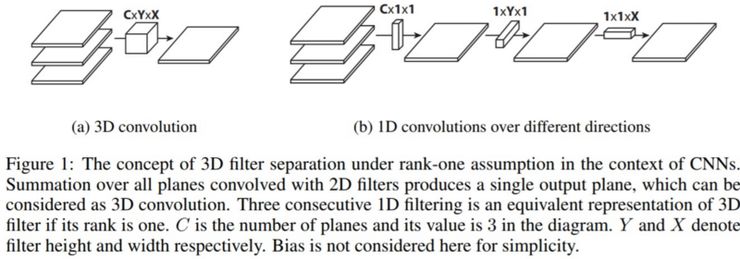
圖片源自：https://arxiv.org/abs/1412.5474

需要注意的一點事，如果標準卷積的過濾器是 rank-1 過濾器，這樣的過濾器可以被拆分為 3 個 1D 過濾器的交叉乘積，但是這是一個前提條件并且標準過濾器的固有 rank 往往比現實應用中的更高。正如論文中所指出的：「隨著分類問題的難度增加，解決該問題還需要更多的關鍵部分... 深度網絡中學習過濾器具有分布的特征值，并且將分離直接用于過濾器會導致明顯的信息丟失。」

為了減輕這類問題，論文限制了感受野的關系從而讓模型可以根據訓練學習 1D 分離的過濾器。這篇論文聲稱，通過使用由連續的 1D 過濾器組成的扁平化網絡在 3D 空間的所有方向上訓練模型，能夠提供的性能與標準卷積網絡相當，不過由于學習參數的顯著減少，其計算成本要更低得多。

10. 分組卷積

2012 年的一篇 AlexNet 論文（ImageNet Classification with Deep Convolutional Neural Networks，https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf）對分組卷積（Grouped convolution）進行了介紹。采用這種卷積的主要原因是為了讓網絡用有限的記憶（1.5GB 記憶/GPU）在兩個 GPU 上進行訓練。下圖的 AlexNet 現實了大部分層的兩條分離的卷積路線，正在進行兩個 GPU 的模型并行化計算。

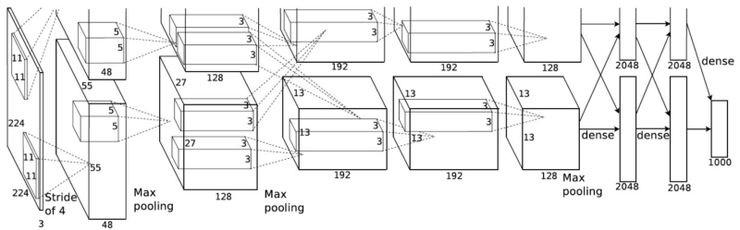
圖片源自：https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf

這里我描述的是分組卷積是如何實現的。首先，傳統的 2D 卷積步驟如下圖所示。在這個案例中，通過應用 128 個過濾器（每個過濾器的大小為 3 x 3 x 3），大小為 7 x 7 x 3 的輸入層被轉換為大小為 5 x 5 x 128 的輸出層。針對通用情況，可概括為：通過應用 Dout 個卷積核（每個卷積核的大小為 h x w x Din），可將大小為 Hin x Win x Din 的輸入層轉換為大小為 Hout x Wout x Dout 的輸出層。

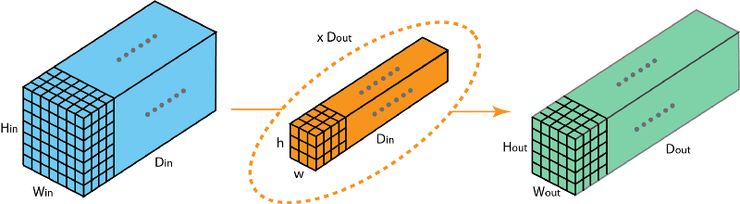
標準 2D 卷積

在分組卷積中，過濾器被拆分為不同的組，每一個組都負責具有一定深度的傳統 2D 卷積的工作。下圖的案例表示得更清晰一些。

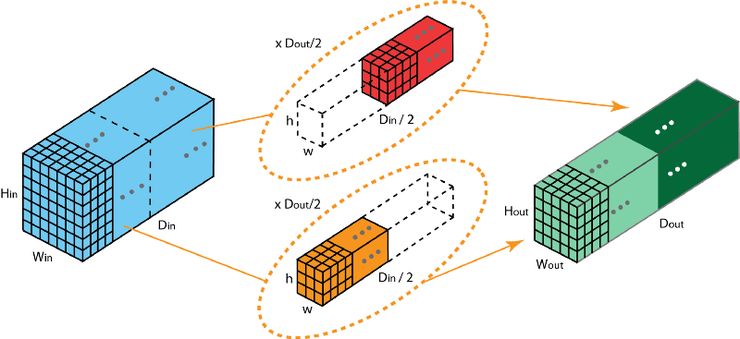
拆分為 2 個過濾組的分組卷積

上圖表示的是被拆分為 2 個過濾器組的分組卷積。在每個過濾器組中，其深度僅為名義上的 2D 卷積的一半（Din / 2），而每個過濾器組都包含 Dout /2 個過濾器。第一個過濾器組（紅色）對輸入層的前半部分做卷積（[:, :, 0:Din/2]），第二個過濾器組（藍色）對輸入層的后半部分做卷積（[:, :, Din/2:Din]）。最終，每個過濾器組都輸出了 Dout/2 個通道。整體上，兩個組輸出的通道數為 2 x Dout/2 = Dout。之后，我們再將這些通道堆疊到輸出層中，輸出層就有了 Dout 個通道。

10.1 分組卷積 VS 深度卷積

你可能已經觀察到了分組卷積和深度可分離卷積中用到的深度卷積之間的某些聯系和區別。如果過濾器組的數量與輸入層的通道數相同，每個過濾器的深度就是 Din / Din = 1，其與深度卷積中的過濾器深度相同。

從另一個角度來說，每個過濾器組現在包含 Dout / Din 個過濾器。總體而言，其輸出層的深度就是 Dout，這就與深度卷積的輸出層深度不同，深度卷積不改變層的深度，但隨后深度可分離卷積中的 1 x 1 卷積會加大層的深度。

執行分組卷積有如下幾個優勢：

第一個優勢是訓練的高效性。由于卷積被拆分到幾條路線中，每條路線都由不同的 GPU 分別進行處理。這一過程就允許模型以平行的方式在多個 GPU 上進行訓練。比起在一個 GPU 上一個一個地訓練模型，這種在多個 GPU 上的模型并行化訓練方式每一步都可以給網絡喂養更多的圖像。模型并行化被認為比數據并行化更佳，后者將數據集進行拆分，然后對每一批數據進行訓練。不過，當每批數據的大小過小時，我們執行的工作基本上是隨機的，而不是批量梯度下降。這就會造成訓練速度變慢或聚合效果變差的結果。

對于訓練非常深度的神經網絡，分組卷積變得很重要，如下圖中 ResNeXt 所示。

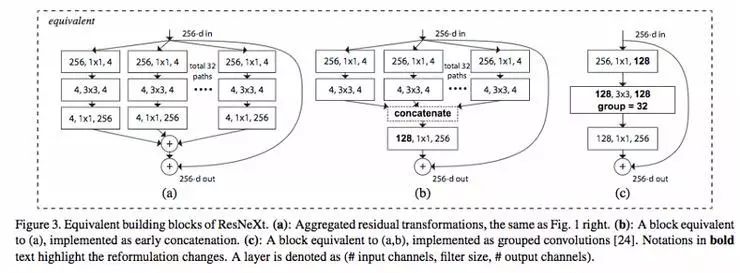
圖片源自：https://arxiv.org/abs/1611.05431

第二個優勢是模型更加高效，例如，當過濾器組數增加時，模型參數就會減少。在前一個案例中，在標準的 2D 卷積中，過濾器有 h x w x Din x Dout 個參數，而在拆分為 2 個過濾器組的分組卷積中，過濾器僅有 (h x w x Din/2 x Dout/2) x 2 個參數：參數數量減少了一半。

第三個優勢是給人帶來了些驚喜的。分組卷積能提供比標準 2D 卷積更好的模型。另一篇很棒的博客「A Tutorial on Filter Groups (Grouped Convolution)」也闡述了這一點。這里僅提取了文章的部分內容，大家可前往https://blog.yani.io/filter-group-tutorial/閱讀全文。

其原因與稀疏的過濾器有關。下面的圖像就是相鄰層的過濾器之間的相互關系，這個關系是稀疏的。

在CIFAR10 訓練的Network-in-Network 模型中相鄰層的過濾器之間的相關性矩陣。高相關的過濾器對更亮，而低相關過濾器對更暗。圖片源自：https://blog.yani.io/filter-group-tutorial/

那面向分組卷積的相關性映射是怎么樣的呢？

當采用 1、2、4、8 和 16 個過濾器組訓練時，在CIFAR10 訓練的Network-in-Network 模型中相鄰層的過濾器之間的相關性。圖片源自：https://blog.yani.io/filter-group-tutorial/

上圖表示的就是模型采用 1、2、4、8 和 16 個過濾器組訓練時，相鄰層的過濾器的相互關系。這篇文章提出了一個推論：「過濾器組的作用就是學習通道維度上的塊對角結構的稀疏性... 在對過濾器進行了分組的網絡中，高相關性的過濾器以更結構化的方式學習。結果，不要求學習的過濾器關系也不再需要用參數進行表示，這就顯著減少了網絡中的參數數量，并且在減少參數的過程中不容易過度擬合，因此這種類似正則化的效果可以讓優化器學習更準確、更有效的深度網絡。」

過濾器分離：正如論文作者所指出的，過濾器組似乎將學習的過濾器拆分成了兩個不同的組：黑白過濾器和彩色過濾器。圖片源自：https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf

此外，每個過濾器組都學習數據獨一無二的表示。正如 AlexaNet 這篇論文的作者所提到的，過濾器組似乎將學習的過濾器拆分成了兩個不同的組：黑白濾鏡和彩色濾鏡。

11. 混洗分組卷積

曠視研究院的 ShuffleNet 論文（ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices，https://arxiv.org/abs/1707.01083）對混洗分組卷積（Shuffled grouped convolution）進行了介紹。ShuffleNet 是一種計算高效的卷積架構，專為計算能力十分有限的移動設備（如 10–150 MFLOPs）設計。

混洗分組卷積背后的思路與分組卷積（應用于 MobileNet 、ResNeXt 等網絡）以及深度可分離卷積（應用于 Xception）背后的思路相關。

總的來說，混洗分組卷積包括分組卷積和通道混洗（channel shuffling）。

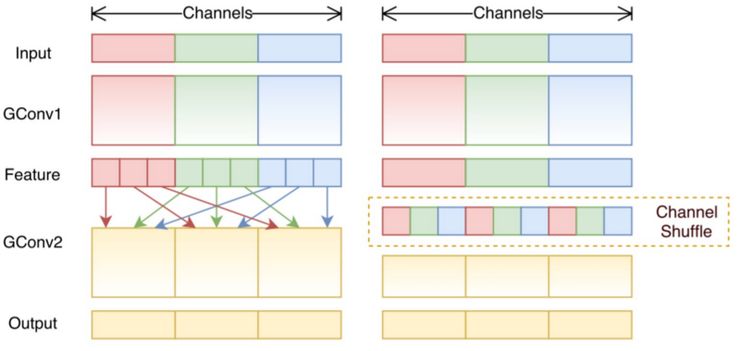
在分組卷積部分，我們了解到了過濾器被拆分為不同的組，每個組都負責擁有一定深度的傳統 2D 卷積的工作，顯著減少了整個操作步驟。在下圖這個案例中，假設過濾器分成了 3 組。第一個過濾器組對輸入層的紅色部分做卷積；第二個和第三個過濾器組分別對輸入層的綠色和藍色部分做卷積。每個過濾器組中的卷積核深度僅為輸入層整個通道的 1/3。在這個案例中，進行第一個分組卷積 GConv1 后，輸入層被映射到中間的特征映射上，之后特征映射又通過第一個分組卷積 GConv2 被映射到輸出層上。

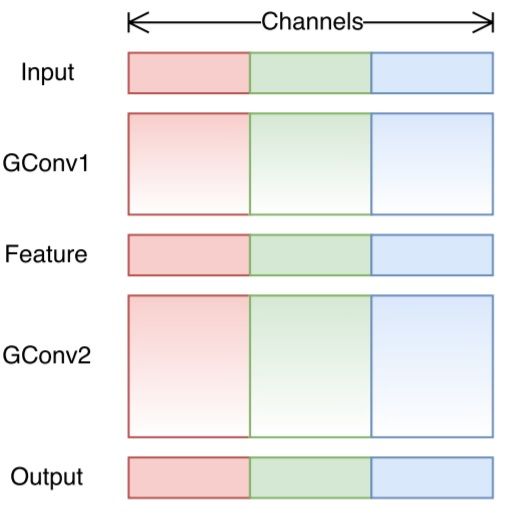
分組卷積雖然計算高效，但它也存在問題，即每個過濾器分組僅對從前面層的固定部分向后傳遞的信息進行處理。在上面這個圖像的案例中，第一個過濾器組（紅色）僅處理從輸入通道的前 1/3 部分向后傳遞的信息；藍色過濾器組僅處理從輸入通道的后 1/3 部分向后傳遞的信息。這樣的話，每個過濾器組就僅限于學習一些特定的特征，這種屬性就阻礙了訓練期間信息在通道組之間流動，并且還削弱了特征表示。為了克服這一問題，我們可以應用通道混洗。

通道混洗的思路就是混合來自不同過濾器組的信息。下圖中，顯示了應用有 3 個過濾器組的第一個分組卷積 GConv1 后所得到的特征映射。在將這些特征映射喂養到第二個分組卷積之前，先將每個組中的通道拆分為幾個小組，然后再混合這些小組。

通道混洗

經過這種混洗，我們再接著如常執行第二個分組卷積 GConv2。但是現在，由于經過混洗的層中的信息已經被混合了，我們本質上是將特征映射層的不同小組喂養給了 GConv2 中的每個組。結果，不僅信息可以在通道組間進行流動，特征表示也得到增強。

12. 逐點分組卷積

ShuffleNet 論文（ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices，https://arxiv.org/abs/1707.01083）同樣也對逐點分組卷積（Pointwise grouped convolution）進行了介紹。一般針對 MobileNet 或 ResNeXt 中的分組卷積，分組在 3x3 的空間卷積而不是 1x1 卷積上執行。

ShuffleNet 這篇論文認為 1x1 卷積的計算成本也很高，提議也對 1x1 卷積進行分組。逐點分組卷積，顧名思義，就是針對 1x1 卷積進行分組操作，這項操作與分組卷積的相同，僅有一項更改——就是在 1x1 過濾器而非 NxN 過濾器 (N>1) 執行。