在學習「數據結構和算法」的過程中，因為人習慣了平鋪直敘的思維方式，所以「遞歸」與「動態規劃」這種帶循環概念（繞來繞去）的往往是相對比較難以理解的兩個抽象知識點。

程序員小吳打算使用動畫的形式來幫助理解「遞歸」，然后通過「遞歸」的概念延伸至理解「動態規劃」算法思想。

什么是遞歸

先下定義：遞歸算法是一種直接或者間接調用自身函數或者方法的算法。

通俗來說，遞歸算法的實質是把問題分解成規模縮小的同類問題的子問題，然后遞歸調用方法來表示問題的解。它有如下特點：

1. 一個問題的解可以分解為幾個子問題的解

2. 這個問題與分解之后的子問題，除了數據規模不同，求解思路完全一樣

3. 存在遞歸終止條件，即必須有一個明確的遞歸結束條件，稱之為遞歸出口

遞歸動畫

通過動畫一個一個特點來進行分析。

1.一個問題的解可以分解為幾個子問題的解

子問題就是相對與其前面的問題數據規模更小的問題。

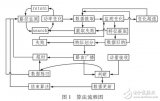
在動圖中①號問題（一塊大區域）劃分為②號問題，②號問題由兩個子問題（兩塊中區域）組成。

2. 這個問題與分解之后的子問題，除了數據規模不同，求解思路完全一樣

「①號劃分為②號」與「②號劃分為③號」的邏輯是一致的，求解思路是一樣的。

3. 存在遞歸終止條件，即存在遞歸出口

把問題分解為子問題，把子問題再分解為子子問題，一層一層分解下去，不能存在無限循環，這就需要有終止條件。

①號劃分為②號，②號劃分為③號，③號劃分為④號，劃分到④號的時候每個區域只有一個不能劃分的問題，這就表明存在遞歸終止條件。

從遞歸的經典示例開始

一.數組求和

數組求和

1Sum(arr[0...n-1])=arr[0]+Sum(arr[1...n-1])

后面的 Sum 函數要解決的就是比前一個 Sum 更小的同一問題。

1Sum(arr[1...n-1])=arr[1]+Sum(arr[2...n-1])

以此類推，直到對一個空數組求和，空數組和為 0 ，此時變成了最基本的問題。

1Sum(arr[n-1...n-1])=arr[n-1]+Sum([])

二.漢諾塔問題

漢諾塔（Hanoi Tower）問題也是一個經典的遞歸問題，該問題描述如下：

漢諾塔問題：古代有一個梵塔，塔內有三個座A、B、C，A座上有64個盤子，盤子大小不等，大的在下，小的在上。有一個和尚想把這個盤子從A座移到B座，但每次只能允許移動一個盤子，并且在移動過程中，3個座上的盤子始終保持大盤在下，小盤在上。

兩個盤子

三個盤子

① 如果只有 1 個盤子，則不需要利用 B 塔，直接將盤子從 A 移動到 C 。

② 如果有 2 個盤子，可以先將盤子 2 上的盤子 1 移動到 B ；將盤子 2 移動到 C ；將盤子 1 移動到 C 。這說明了：可以借助 B 將 2 個盤子從 A 移動到 C ，當然，也可以借助 C 將 2 個盤子從 A 移動到 B 。

③ 如果有 3 個盤子，那么根據 2 個盤子的結論，可以借助 C 將盤子 3 上的兩個盤子從 A 移動到 B ；將盤子 3 從 A 移動到 C ，A 變成空座；借助 A 座，將 B 上的兩個盤子移動到 C 。

④ 以此類推，上述的思路可以一直擴展到 n 個盤子的情況，將將較小的 n-1個盤子看做一個整體，也就是我們要求的子問題，以借助 B 塔為例，可以借助空塔 B 將盤子A上面的 n-1 個盤子從 A 移動到 B ；將A 最大的盤子移動到 C ， A 變成空塔；借助空塔 A ，將 B 塔上的 n-2 個盤子移動到 A，將 B 最大的盤子移動到 C， B 變成空塔。。。

三.爬臺階問題

問題描述：

一個人爬樓梯，每次只能爬1個或2個臺階，假設有n個臺階，那么這個人有多少種不同的爬樓梯方法？

先從簡單的開始，以 4 個臺階為例，可以通過每次爬 1 個臺階爬完樓梯：

每次爬 1 個臺階

可以通過先爬 2 個臺階，剩下的每次爬 1 個臺階爬完樓梯

先爬 2 個臺階

在這里，可以思考一下：可以根據第一步的走法把所有走法分為兩類：

① 第一類是第一步走了 1 個臺階

② 第二類是第一步走了 2 個臺階

所以 n 個臺階的走法就等于先走 1 階后，n-1 個臺階的走法 ，然后加上先走 2 階后，n-2 個臺階的走法。

用公式表示就是：

f(n) = f(n-1)+f(n-2)

有了遞推公式，遞歸代碼基本上就完成了一半。那么接下來考慮遞歸終止條件。

當有一個臺階時，我們不需要再繼續遞歸，就只有一種走法。

所以 f(1)=1。

通過用 n = 2，n = 3 這樣比較小的數試驗一下后發現這個遞歸終止條件還不足夠。

n = 2 時，f(2) = f(1) + f(0)。如果遞歸終止條件只有一個f(1) = 1，那 f(2) 就無法求解，遞歸無法結束。 所以除了 f(1) = 1 這一個遞歸終止條件外，還要有 f(0) = 1，表示走 0 個臺階有一種走法，從思維上以及動圖上來看，這顯得的有點不符合邏輯。所以為了便于理解，把 f(2) = 2 作為一種終止條件，表示走 2 個臺階，有兩種走法，一步走完或者分兩步來走。

總結如下：

① 假設只有一個臺階，那么只有一種走法，那就是爬 1 個臺階

② 假設有兩個個臺階，那么有兩種走法，一步走完或者分兩步來走

遞歸終止條件

通過遞歸條件：

1f(1)=1;2f(2)=2;3f(n)=f(n-1)+f(n-2)

很容易推導出遞歸代碼：

1intf(intn){2if(n==1)return1;3if(n==2)return2;4returnf(n-1)+f(n-2);5}

通過上述三個示例，總結一下如何寫遞歸代碼：

1.找到如何將大問題分解為小問題的規律

2.通過規律寫出遞推公式

3.通過遞歸公式的臨界點推敲出終止條件

4.將遞推公式和終止條件翻譯成代碼

什么是動態規劃

介紹動態規劃之前先介紹一下分治策略（Divide and Conquer）。

分治策略

將原問題分解為若干個規模較小但類似于原問題的子問題（Divide），「遞歸」的求解這些子問題（Conquer），然后再合并這些子問題的解來建立原問題的解。

因為在求解大問題時，需要遞歸的求小問題，因此一般用「遞歸」的方法實現，即自頂向下。

動態規劃（Dynamic Programming）

動態規劃其實和分治策略是類似的，也是將一個原問題分解為若干個規模較小的子問題，遞歸的求解這些子問題，然后合并子問題的解得到原問題的解。 區別在于這些子問題會有重疊，一個子問題在求解后，可能會再次求解，于是我們想到將這些子問題的解存儲起來，當下次再次求解這個子問題時，直接拿過來就是。 其實就是說，動態規劃所解決的問題是分治策略所解決問題的一個子集，只是這個子集更適合用動態規劃來解決從而得到更小的運行時間。 即用動態規劃能解決的問題分治策略肯定能解決，只是運行時間長了。因此，分治策略一般用來解決子問題相互對立的問題，稱為標準分治，而動態規劃用來解決子問題重疊的問題。

與「分治策略」「動態規劃」概念接近的還有「貪心算法」「回溯算法」，由于篇幅限制，程序員小吳就不在這進行展開，在后續的文章中將分別詳細的介紹「貪心算法」、「回溯算法」、「分治算法」，敬請關注：）

將「動態規劃」的概念關鍵點抽離出來描述就是這樣的：

1.動態規劃法試圖只解決每個子問題一次

2.一旦某個給定子問題的解已經算出，則將其記憶化存儲，以便下次需要同一個子問題解之時直接查表。

從遞歸到動態規劃

還是以爬臺階為例，如果以遞歸的方式解決的話，那么這種方法的時間復雜度為O(2^n)，具體的計算可以查看筆者之前的文章 《冰與火之歌：時間復雜度與空間復雜度》。

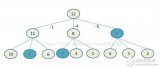
相同顏色代表著 爬臺階問題 在遞歸計算過程中重復計算的部分。

爬臺階的時間復雜度

通過圖片可以發現一個現象，我們是 自頂向下 的進行遞歸運算，比如：f(n) 是f(n-1)與f(n-2)相加，f(n-1) 是f(n-2)與f(n-3)相加。

思考一下：如果反過來，采取自底向上，用迭代的方式進行推導會怎么樣了？

下面通過表格來解釋 f(n)自底向上的求解過程。

臺階數	1	2	3	4	5	6	7	8	9
走法數	1	2

表格的第一行代表了樓梯臺階的數目，第二行代表了若干臺階對應的走法數。其中f(1) = 1 和 f(2) = 2是前面明確的結果。

第一次迭代，如果臺階數為 3 ，那么走法數為 3 ，通過 f(3) = f(2) + f(1)得來。

臺階數	1	2	3	4	5	6	7	8	9
走法數	1	2	3

第二次迭代，如果臺階數為 4 ，那么走法數為 5 ，通過 f(4) = f(3) + f(2)得來。

臺階數	1	2	3	4	5	6	7	8	9
走法數	1	2	3	5

由此可見，每一次迭代過程中，只需要保留之前的兩個狀態，就可以推到出新的狀態。

show me the code

1intf(intn){ 2if(n==1)return1; 3if(n==2)return2; 4//a保存倒數第二個子狀態數據，b保存倒數第一個子狀態數據，temp保存當前狀態的數據 5inta=1,b=2; 6inttemp=a+b; 7for(inti=3;i<=?n;?i++)?{ 8????????temp?=?a?+?b; 9????????a?=?b;10????????b?=?temp;?11????}12????return?temp;?13}

程序從 i = 3 開始迭代，一直到 i = n 結束。每一次迭代，都會計算出多一級臺階的走法數量。迭代過程中只需保留兩個臨時變量 a 和 b ，分別代表了上一次和上上次迭代的結果。為了便于理解，引入了temp變量。temp代表了當前迭代的結果值。

看一看出，事實上并沒有增加太多的代碼，只是簡單的進行了優化，時間復雜度便就降為O(n)，而空間復雜度也變為O(1)，這，就是「動態規劃」的強大！

詳解動態規劃

「動態規劃」中包含三個重要的概念：

【最優子結構】

【邊界】

【狀態轉移公式】

在「 爬臺階問題 」中

f(10) = f(9) + f(8) 是【最優子結構】 f(1) 與 f(2) 是【邊界】 f(n) = f(n-1) + f(n-2) 【狀態轉移公式】

「 爬臺階問題 」 只是動態規劃中相對簡單的問題，因為它只有一個變化維度，如果涉及多個維度的話，那么問題就變得復雜多了。

難點就在于找出 「動態規劃」中的這三個概念。

比如「 國王和金礦問題 」。

國王和金礦問題

有一個國家發現了 5 座金礦，每座金礦的黃金儲量不同，需要參與挖掘的工人數也不同。參與挖礦工人的總數是 10 人。每座金礦要么全挖，要么不挖，不能派出一半人挖取一半金礦。要求用程序求解出，要想得到盡可能多的黃金，應該選擇挖取哪幾座金礦？

5 座金礦

找出 「動態規劃」中的這三個概念

國王和金礦問題中的【最優子結構】

國王和金礦問題中的【最優子結構】

國王和金礦問題中的【最優子結構】有兩個：

① 4 金礦 10 工人的最優選擇

② 4 金礦 （10 - 5） 工人的最優選擇

4 金礦的最優選擇與 5 金礦的最優選擇之間的關系是

MAX[（4 金礦 10 工人的挖金數量），（4 金礦 5 工人的挖金數量 + 第 5 座金礦的挖金數量）]

國王和金礦問題中的【邊界】

國王和金礦問題中的【邊界】 有兩個：

① 當只有 1 座金礦時，只能挖這座唯一的金礦，得到的黃金數量為該金礦的數量

② 當給定的工人數量不夠挖 1 座金礦時，獲取的黃金數量為 0

國王和金礦問題中的【狀態轉移公式】

我們把金礦數量設為 N，工人數設為 W，金礦的黃金量設為數組G[]，金礦的用工量設為數組P[]，得到【狀態轉移公式】：

邊界值：F(n,w) = 0 (n <= 1, w < p[0])

F(n,w) = g[0] (n==1, w >= p[0])

F(n,w) = F(n-1,w) (n > 1, w < p[n-1])

F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1]) + g[n-1]) (n > 1, w >= p[n-1])

國王和金礦問題中的【實現】

先通過幾幅動畫來理解 「工人」 與 「金礦」 搭配的方式

1.只挖第一座金礦

只挖第一座金礦

在只挖第一座金礦前面兩個工人挖礦收益為 零，當有三個工人時，才開始產生收益為 200，而后即使增加再多的工人收益不變，因為只有一座金礦可挖。

2.挖第一座與第二座金礦

挖第一座金礦與第二座金礦

在第一座與第二座金礦這種情況中，前面兩個工人挖礦收益為 零，因為 W < 3,所以F(N,W) = F(N-1,W) = 0。

當有 三 個工人時，將其安排挖第 一 個金礦，開始產生收益為 200。

當有 四 個工人時，挖礦位置變化，將其安排挖第 二 個金礦，開始產生收益為 300。

當有 五、六 個工人時，由于多于 四 個工人的人數不足以去開挖第 一 座礦，因此收益還是為 300。

當有 七 個工人時，可以同時開采第 一 個和第 二 個金礦，開始產生收益為 500。

3.挖前三座金礦

這是「國王和金礦」 問題中最重要的一個動畫之一，可以多看幾遍

挖前三座金礦

4.挖前四座金礦

這是「國王和金礦」 問題中最重要的一個動畫之一，可以多看幾遍

挖前四座金礦

國王和金礦問題中的【規律】

仔細觀察上面的幾組動畫可以發現：

對比「挖第一座與第二座金礦」和「挖前三座金礦」，在「挖前三座金礦」中，3 金礦 7 工人的挖礦收益，來自于 2 金礦 7 工人和 2 金礦 4 工人的結果，Max(500,300 + 350) = 650；

對比「挖前三座金礦」和「挖前四座金礦」，在「挖前四座金礦」中，4 金礦 10 工人的挖礦收益，來自于 3 金礦 10 工人和 3 金礦 5 工人的結果，Max(850,400 + 300) = 850；

國王和金礦問題中的【動態規劃代碼】

1代碼來源：https://www.cnblogs.com/SDJL/archive/2008/08/22/1274312.html 2 3//maxGold[i][j]保存了i個人挖前j個金礦能夠得到的最大金子數，等于-1時表示未知 4intmaxGold[max_people][max_n]; 5 6intGetMaxGold(intpeople,intmineNum){ 7intretMaxGold;//聲明返回的最大金礦數量 8//如果這個問題曾經計算過 9if(maxGold[people][mineNum]!=-1){10retMaxGold=maxGold[people][mineNum];//獲得保存起來的值11}elseif(mineNum==0){//如果僅有一個金礦時[對應動態規劃中的"邊界"]12if(people>=peopleNeed[mineNum])//當給出的人數足夠開采這座金礦13retMaxGold=gold[mineNum];//得到的最大值就是這座金礦的金子數14else//否則這唯一的一座金礦也不能開采15retMaxGold=0;//得到的最大值為0個金子16}elseif(people>=peopleNeed[mineNum])//如果人夠開采這座金礦[對應動態規劃中的"最優子結構"]17{18//考慮開采與不開采兩種情況，取最大值19retMaxGold=max(20GetMaxGold(people-peopleNeed[mineNum],mineNum-1)+gold[mineNum],21GetMaxGold(people,mineNum-1)22);23}else//否則給出的人不夠開采這座金礦[對應動態規劃中的"最優子結構"]24{25retMaxGold=GetMaxGold(people,mineNum-1);//僅考慮不開采的情況26maxGold[people][mineNum]=retMaxGold;27}28returnretMaxGold;29}

動態規劃代碼