被數(shù)學(xué)題難倒的AI。

做數(shù)學(xué)題一直令多數(shù)人頭疼不已的事情。近期，DeepMind團(tuán)隊(duì)最新研究了利用AI來解數(shù)學(xué)題，但結(jié)果令人大跌眼鏡——水平不及高中生。

數(shù)學(xué)也難倒了AI。

數(shù)學(xué)可能是大多數(shù)人在求學(xué)過程中最頭疼的一門科目。近日，DeepMind團(tuán)隊(duì)便對(duì)“AI做數(shù)學(xué)題”進(jìn)行了研究，結(jié)果大跌眼鏡：“萬能的AI”在面對(duì)數(shù)學(xué)問題也是不知所措！

人類解題能力超群的關(guān)鍵在于，人類并非主要通過經(jīng)驗(yàn)和證據(jù)，而是通過推斷、學(xué)習(xí)，以及利用定理、公理和符號(hào)操縱規(guī)則。

DeepMind團(tuán)隊(duì)便對(duì)神經(jīng)架構(gòu)和類似系統(tǒng)的評(píng)估（以及最終的設(shè)計(jì)）提出了新的挑戰(zhàn)，開發(fā)了一個(gè)數(shù)學(xué)問題的任務(wù)處理套件，涉及以自由形式文本輸入/輸出格式的系列問題和答案。

不過，在研究過程中，DeepMind發(fā)現(xiàn)，AI非常擅長做的數(shù)學(xué)題都是比較偏簡單的，例如：查找數(shù)字中的位值、四舍五入小數(shù)/整數(shù)等。但是在諸如素?cái)?shù)檢測、因式分解以及多項(xiàng)式操作等方面，性能結(jié)果存在顯著的差異。

AI做數(shù)學(xué)的能力不及高中生水平？

AI挑戰(zhàn)人類最難學(xué)科

深層模型遠(yuǎn)未達(dá)到人類所表現(xiàn)出的穩(wěn)健性和靈活性，由于自身能力的限制，深度學(xué)習(xí)無法超越所經(jīng)歷的環(huán)境去生成新的東西，并且面對(duì)存在對(duì)抗性構(gòu)建的輸入時(shí)極其脆弱。

與神經(jīng)模型相比，人類智能擅長的一個(gè)領(lǐng)域是關(guān)于物體和實(shí)體的離散組合推理，即“代數(shù)泛化”，這個(gè)領(lǐng)域也體現(xiàn)了神經(jīng)模型和人類智之間的差異。

人類在這個(gè)領(lǐng)域內(nèi)的概括能力是復(fù)雜的、多方面的。先來看這個(gè)數(shù)學(xué)題：

當(dāng)：f(x)= 2x + 3，g(x)= 7x-4，h(x)= -5x-8時(shí)

求：g(h(f(x)))

人類解決這道數(shù)學(xué)題時(shí)候，用到的各種認(rèn)知技能有：

將字符解析為數(shù)字，算術(shù)運(yùn)算符，變量（一起形成函數(shù)）和單詞（確定問題）等實(shí)體

計(jì)劃（例如，以正確的順序識(shí)別功能以進(jìn)行撰寫）

使用子算法進(jìn)行函數(shù)合成（加法，乘法）

利用工作記憶來存儲(chǔ)中間值（例如合成h(f(x))）

通常應(yīng)用已獲得的規(guī)則，轉(zhuǎn)換，過程和公理知識(shí)

DeepMind在這篇論文中引入了一個(gè)由許多不同類型的數(shù)學(xué)問題組成的數(shù)據(jù)集，對(duì)于模型來說，優(yōu)于缺乏上述人類能力，在處理跨系列的問題類型（包括我們?cè)谙旅嬖斒龅姆夯┑臅r(shí)候難度更大，更難獲得良好的表現(xiàn)。

該領(lǐng)域?qū)τ谝话愕纳窠?jīng)結(jié)構(gòu)的分析是重要的。除了提供廣泛的問題外，還有其他幾個(gè)優(yōu)點(diǎn)：

數(shù)學(xué)提供了一個(gè)自洽的宇宙(self-consistent universe)；

符號(hào)在不同的問題類型中是相同的，是的數(shù)據(jù)集更容易得到擴(kuò)展的；

在一種問題類型上學(xué)習(xí)的規(guī)則和方法通常適用于其他地方。例如數(shù)字的加法在任何地方都遵循相同的規(guī)則，并且在其他問題中作為“子程序”出現(xiàn)，具體體現(xiàn)在乘法中，以及具體且更抽閑的體現(xiàn)在多項(xiàng)式中；

具有轉(zhuǎn)移知識(shí)能力的模型將在數(shù)據(jù)集上獲得更好的表現(xiàn)（知識(shí)遷移可能是解決更難問題的必要條件）。

數(shù)學(xué)本身也是一個(gè)有趣的領(lǐng)域，雖然解決該數(shù)據(jù)集中大多數(shù)中學(xué)數(shù)學(xué)問題的模型本身不具備應(yīng)用程序，但它們可能會(huì)導(dǎo)致更強(qiáng)大的模型，這些模型可以解決有趣且實(shí)質(zhì)性的新數(shù)學(xué)問題。

或者更一般地說，尋求驗(yàn)證以捕獲算法/系統(tǒng)推理為目標(biāo)的新架構(gòu)的實(shí)驗(yàn)經(jīng)常從這個(gè)領(lǐng)域中得出，這并非巧合。因此，在為這些模型提供大規(guī)模的訓(xùn)練和評(píng)估框架時(shí)，希望為繼續(xù)研究超越數(shù)學(xué)的機(jī)器推理提供堅(jiān)實(shí)的基礎(chǔ)。

請(qǐng)看以下數(shù)學(xué)問題集示例：

問題：對(duì)于r，求解-42*r+27*c=-1167和130*r+4*c=372。

答案：4

問題：計(jì)算-841880142.544+411127。

答案：-841469015.544

問題：Letx(g)=9*g+1。Letq(C)=2*C+1。Letf(i)=3*i-39.設(shè)w(j)=q(x(j))。計(jì)算f(w(a))。

答案：54*a-30

問題：設(shè)e(l)=l-6.2是e(9)和2的因子嗎？

答案：錯(cuò)

問題：設(shè)u(n)=-n**3-n**2。設(shè)e(c)=-2*c**3+c。令l(j)=-118*e(j)+54*u(j)。l(a)的衍生物是什么？

答案：546*a**2-108*a-118

問題：從qqqkkklkqkkk中選擇了三個(gè)字母而沒有替換。給出序列qql的概率

答案：1/110

研究中的主要貢獻(xiàn)

數(shù)據(jù)集和泛化測試

研究人員發(fā)布1個(gè)序列到序列的數(shù)據(jù)集，包括許多不同類型的數(shù)學(xué)問題（見圖1），用于測量數(shù)學(xué)推理，同時(shí)提供生成代碼和預(yù)生成的問題。

數(shù)據(jù)集附帶兩組測試：插值測試，一個(gè)針對(duì)訓(xùn)練集中出現(xiàn)的每種類型的問題；外推測試，測量沿著各種難度軸的概括超出訓(xùn)練期間的概括。將外推測試作為模型是否采用允許它們進(jìn)行代數(shù)泛化的能力的額外度量。

實(shí)驗(yàn)和模型分析

本文利用一個(gè)實(shí)驗(yàn)評(píng)估來研究最先進(jìn)的神經(jīng)架構(gòu)的代數(shù)能力，實(shí)驗(yàn)表明它們?cè)谀承╊愋偷膯栴}上表現(xiàn)良好，但肯定不是全部，而且只有適度的數(shù)量一般化。我們對(duì)他們?nèi)绾螌W(xué)習(xí)回答數(shù)學(xué)問題及其失敗模式提供了一些見解。

由于該數(shù)據(jù)集背后的構(gòu)建過程，有大量現(xiàn)有模型可以進(jìn)行調(diào)整、專門構(gòu)建或定制，以解決提出的問題，特別是在符號(hào)求解器或計(jì)算機(jī)代數(shù)系統(tǒng)的幫助下。

模型檢驗(yàn)

隨著問題和答案的復(fù)雜性或語言多樣性的增長，撇開傳統(tǒng)符號(hào)方法可能的脆弱性或可擴(kuò)展性的限制，我們對(duì)評(píng)估通用模型更感興趣，而非已經(jīng)內(nèi)置數(shù)學(xué)知識(shí)的模型。

使這些模型（總是神經(jīng)架構(gòu)）從翻譯到通過圖像字幕解析無處不在的原因，是這些函數(shù)逼近器缺乏偏差，因?yàn)樗鼈兊脑O(shè)計(jì)中編碼的域特定知識(shí)相對(duì)較少（或沒有）。

雖然有一些神經(jīng)網(wǎng)絡(luò)驅(qū)動(dòng)的方法可以直接訪問數(shù)學(xué)運(yùn)算（例如加法或乘法，或更復(fù)雜的數(shù)學(xué)模板，這無疑是我們?cè)诒疚闹刑岢龅娜蝿?wù)中具有競爭力，我們將局限于一般的序列處理架構(gòu)，這些架構(gòu)用于其他非數(shù)學(xué)任務(wù)，以便為將來的比較提供最一般的基準(zhǔn)。

論文研究了兩種（廣泛的）模型，這些模型已經(jīng)證明了它們?cè)谛蛄械叫蛄袉栴}上的最新技術(shù)：循環(huán)神經(jīng)架構(gòu)，以及最近引入的Attention/Transfomer結(jié)構(gòu)。 我們還嘗試使用可微分神經(jīng)計(jì)算機(jī)，這是一種具有“外部存儲(chǔ)器”的復(fù)現(xiàn)模型（其大小與網(wǎng)絡(luò)中的參數(shù)數(shù)量無關(guān)）。

理論上，這可能非常適合解決數(shù)學(xué)問題，因?yàn)樗梢源鎯?chǔ)中間值以供以后使用。然而，卻無法從中獲得不錯(cuò)的表現(xiàn)，即使對(duì)于內(nèi)存插槽的數(shù)量和大小的超參數(shù)掃描等，在訓(xùn)練一天后才能達(dá)到10％的驗(yàn)證性能，而大多數(shù)模型在不到一個(gè)小時(shí)內(nèi)就能獲得這一點(diǎn)。

圖2：注意力LSTM和Transformer體系結(jié)構(gòu)都包含一個(gè)解析問題的編碼器和一個(gè)解碼器，它將正確的答案右移1個(gè)映射到每個(gè)位置的答案中的下一個(gè)字符（因此允許自回歸預(yù)測）：

(a)注意LSTM將問題編碼為一系列（關(guān)鍵，值）位置，然后由解碼器進(jìn)行處理

(b)變壓器有幾個(gè)階段的自我注意和輸入注意

循環(huán)結(jié)構(gòu)

LSTM 是一個(gè)強(qiáng)大的序列到序列模型構(gòu)建模塊，它在許多領(lǐng)域都達(dá)到了最先進(jìn)的結(jié)果，盡管它很簡單，但仍然是循環(huán)神經(jīng)網(wǎng)絡(luò)的一個(gè)核心構(gòu)建模塊。本文測試了兩個(gè)標(biāo)準(zhǔn)的循環(huán)結(jié)構(gòu)。

第一個(gè)(也是最簡單)模型，稱作“Simple LSTM”是直接將問題提交到LSTM，一次輸入一個(gè)字符(采用1-hot編碼)；

第二個(gè)模型稱作“Attentionnal LSTM”，是引入具有注意力結(jié)構(gòu)的編碼器/解碼器。

在這兩種體系結(jié)構(gòu)中，還使用了一個(gè)簡單的更改來提高性能。所描述的模型必須在解析問題之后直接輸出答案。

近期，一種稱為關(guān)系遞歸神經(jīng)網(wǎng)絡(luò)或關(guān)系內(nèi)存核(relational memory core，RMC)的遞歸體系結(jié)構(gòu)被開發(fā)出來作為LSTM的替代品。這個(gè)重復(fù)單元有多個(gè)記憶槽，它們通過注意力相互作用。

TRANSFORMER

Transformer模型是一個(gè)實(shí)現(xiàn)機(jī)器翻譯的最先進(jìn)結(jié)果的序列到序列模型。圖2b對(duì)其做了簡要的描述。該模型由編碼器和解碼器組成，前者將問題(表示為向量序列)轉(zhuǎn)換為另一個(gè)相同長度的序列，后者將編碼的問題和答案轉(zhuǎn)換為答案預(yù)測。

性能分析

訓(xùn)練和評(píng)估方法

與序列到序列模型中常見的方法一樣，這些模型使用貪婪解碼器(每一步輸出多數(shù)類)自回歸地預(yù)測答案。通過Adam優(yōu)化器最小化正確字符的對(duì)數(shù)概率之和，學(xué)習(xí)率為6×10-4，β1= 0.9，β2= 0.995，ε= 10-9。 使用批量大小為1024的8個(gè)NVIDIA P100 GPU進(jìn)行500k批次分割，絕對(duì)梯度值限幅為0.1。

實(shí)驗(yàn)結(jié)果

圖3顯示了不同結(jié)構(gòu)的平均插值和外推(extrapolation)性能。

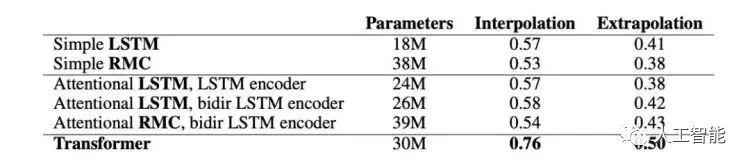
圖3模型精度(正確答案的概率)在各個(gè)模塊之間取平均值。RMC是關(guān)系遞歸神經(jīng)網(wǎng)絡(luò)模型。

LSTMs vs RMCs

使用具有多個(gè)內(nèi)存插槽的RMC不會(huì)提高性能；也許RMC很難學(xué)會(huì)使用插槽來操縱數(shù)學(xué)實(shí)體。對(duì)于給定數(shù)量的隱含單元，RMC的數(shù)據(jù)效率更高，但訓(xùn)練速度更慢(因?yàn)樗鼈冇懈嗟膮?shù))，LSTMs具有更好的漸近性能。

Simple vs Attentional LSTM

Attentional LSTM和Simple LSTM具有相似的性能。有人可能會(huì)懷疑Attentional LSTM什么也不做，但事實(shí)并非如此，因?yàn)榕c解析LSTM大小相同的Simple LSTM模型獲得的性能要差得多。我們推測，注意力模型并沒有學(xué)習(xí)算法解析問題，因此每一步改變注意力焦點(diǎn)的能力并不重要。

“思考”步驟數(shù)

對(duì)于Attentional LSTM模型，可以觀察到，將“思考”步驟的數(shù)量從0增加到16，可以提高性能。

Transformer vs 最好的非transformer模型

Transformer在幾乎所有模塊上的性能與遞歸模型相同，或者明顯優(yōu)于遞歸模型。這兩種體系結(jié)構(gòu)具有相當(dāng)數(shù)量的參數(shù)。人們可能會(huì)預(yù)先期望LSTM執(zhí)行得更好，因?yàn)樗捻樞蝮w系結(jié)構(gòu)可能更類似于人類執(zhí)行的順序推理步驟。然而，實(shí)驗(yàn)表明，這兩種網(wǎng)絡(luò)都沒有做太多的“算法推理”，并且Transformer相對(duì)于LSTM架構(gòu)具有各種優(yōu)勢，例如：

使用相同數(shù)量的參數(shù)進(jìn)行更多計(jì)算；

具有更好的梯度傳播；

有一個(gè)內(nèi)部連續(xù)的“記憶”。

對(duì)神經(jīng)網(wǎng)絡(luò)來說最簡單的數(shù)學(xué)問題

最簡單的問題類型是查找數(shù)字中的位值，以及四舍五入小數(shù)和整數(shù)，所有模型在這些方面都獲得了近乎完美的分?jǐn)?shù)。涉及比較的問題也往往相當(dāng)容易，因?yàn)檫@類任務(wù)是相當(dāng)感性的(例如比較長度或單個(gè)數(shù)字)。

對(duì)神經(jīng)網(wǎng)絡(luò)來說最困難的數(shù)學(xué)問題

也許并不奇怪，一些最難的模塊包含了更多的數(shù)字理論問題，這些問題對(duì)人類來說也很難，比如檢測素?cái)?shù)和因式分解。

Transformer模型在“加或減幾個(gè)數(shù)字”模塊和“乘數(shù)或除數(shù)”模塊的性能為90％或更高。然而，在混合算術(shù)模塊上，性能下降到大約50％。我們推測這些模塊之間的區(qū)別在于前者可以在相對(duì)線性/淺/平行的方式（因此解決方法通過梯度下降相對(duì)容易發(fā)現(xiàn)），而沒有用括號(hào)評(píng)估混合算術(shù)表達(dá)式的快捷方式，其中需要計(jì)算中間值。

這證明模型沒有學(xué)習(xí)任何代數(shù)/算法操作值，而是學(xué)習(xí)相對(duì)簡單的技巧來獲得許多模塊的良好答案。對(duì)于其他需要中間值計(jì)算的模塊，如多項(xiàng)式求值和一般組合，也是如此。

多項(xiàng)式操縱性能

Transformer和遞歸模型之間的一個(gè)顯著差異是多項(xiàng)式操作。Transformer在多項(xiàng)式展開、收集項(xiàng)、加法、組合、微分和提取命名系數(shù)方面做得明顯更好。從理論上說，Transformer的并行順序特性更擅長于處理多項(xiàng)式，其中幾個(gè)系數(shù)必須同時(shí)保存在內(nèi)存中，以便相互作用。