本文對離散信號的頻域分析(共5節)中的第4節——快速傅里葉變換FFT(Fast- Fourier Transform)進行串講。

首先大家需要知道的是,FFT并不是一種新的變換,它僅僅是作為DFT的快速算法。本節包括下列內容:

4.1 改進DFT計算的方法
1. DFT計算量分析

觀察正變換和反變換的公式可知,二者的運算方式和運算量是完全相同的。下面的分析均以DFT正變換為例。(順便說一句,大家要像熟悉自己的手機一樣熟悉旋轉因子,閉著眼睛都知道它)
觀察DFT正變換的公式,容易看出:每計算一個點的數據,需要N次復數乘法、N-1次復數加法,所以,N點DFT,需要N的平方次復數乘法,N(N-1)次復數加法。我們知道,DFT的點數,至少要取成序列的長度,當序列長度很長時,運算量巨大!如下圖所示。
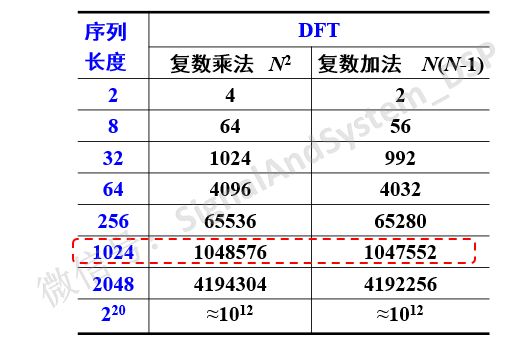
以1024點為例,復數乘法的次數100萬次之多。
1965年,庫利(J.W.Cooley)和圖基(J.W.Tukey)在《Mathmatics of Computation》上發表了《AnAlgorithm for the Machine Calculation of Complex Fourier Series》,提出一種高效DFT運算的快速算法,后人稱為快速傅里葉變換(Fast Fourier Transform ——FFT)。
2. 改進DFT計算效率的基本途徑
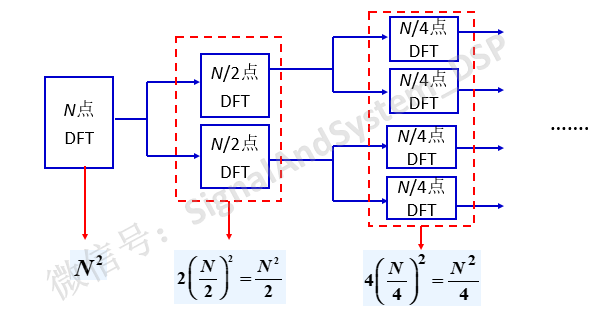
N點DFT,直接計算,需要N的平方次乘法;分成2個N/2點DFT分別計算,乘法的次數是1/2的N的平方,減少了一半;分成4個N/4點DFT,乘法的次數又減少了一半。如果能夠繼續下去,前景很讓人向往。
為了能夠一直分下去,我們限定N為2的整數次冪,即:N=2^M,稱為基2FFT。
由此可見,FFT的基本思想是:把長序列分成幾個較短的序列。
但怎么分?不能隨便亂分,基本原則是:要保證這幾個短序列的DFT組合起來后,能夠很方便地構成原來長序列的DFT。
所以,DFT快速算法要解決的兩個核心問題是:怎么分?怎么合?
根據分與合的方式不同,有兩種基2FFT算法,分別稱為:
按時間抽取的FFT算法——Decimation-in-Time,簡稱DIT-FFT。
按頻率抽取的FFT算法——Decimation-in-Frequency,簡稱DIF-FFT。
下面我們分別來歸納總結兩種基2FFT算法。
4.2 兩種基2FFT算法
1. 按時間抽取(DIT)FFT算法
以第一次分解(N點分為2個N/2點)為例來說明算法原理。
首先解決怎么分的問題。

通俗地說,就是:大家列隊、報數(從0開始)。報偶數的一組,奇數的一組。

然后解決怎么合的問題。
我們略過看似艱苦卓絕實際很簡單的推導過程,直接上結論:

公式不好看,有人畫了一幅圖,并且起了個好聽的名字:蝶形運算符號。
下面的動圖演示了蝶形運算的過程:

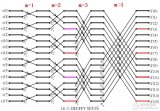
以8點長序列為例,我們來看分解為2個4點長DFT,是如何通過蝶形運算合成8點DFT的:

經過第一次分解之后,總的運算量=兩個N/2點DFT的運算+N/2個蝶形的運算。而每次蝶形運算,只需要1次乘法,2次加法。所以,總的乘法次數為
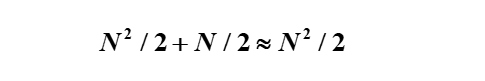
加法次數為
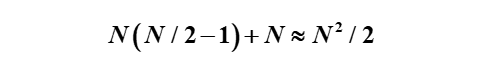
當N很大時,運算量減少了近一半。
這就給了我們信心,說明這種分解思路是可以有效減少運算量的。我們繼續分解下去,經過M-1次分解,分解為N/2 個 2 點長序列。
而2點DFT也用蝶形運算來表示(因為計算機最擅長一致而重復的東西),就得到下面的流圖:
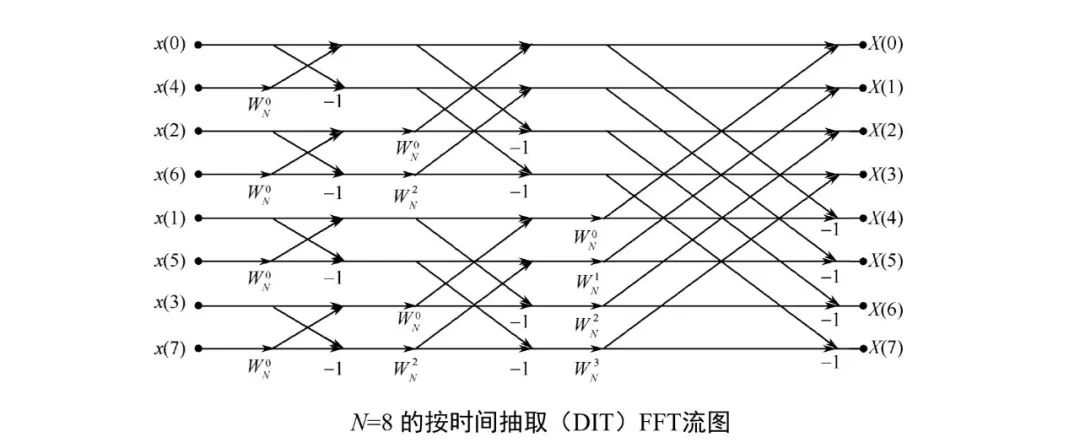
2. 按頻率抽取(DIF)FFT算法
仍以第一次分解(N點分為2個N/2點)為例來說明算法原理。
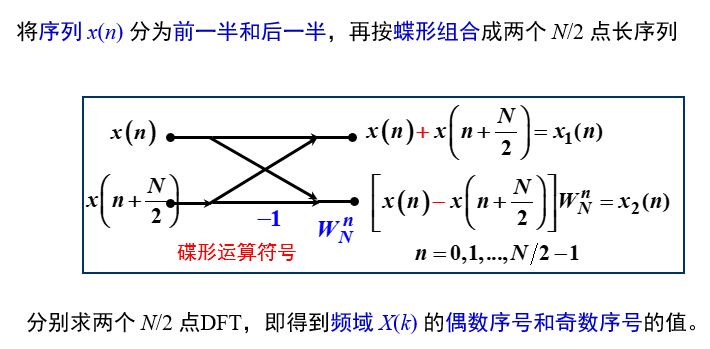
以8點長序列為例,我們來看分解為2個4點長DFT,是如何通過蝶形運算合成8點DFT的:

注意到,輸出的頻率數據,序號是按照偶數一組、奇數一組的順序排列的,所以這種算法稱為:按頻率抽取。
我們繼續分解下去,經過M-1次分解,分解為N/2 個 2 點長序列,就得到下面的流圖:
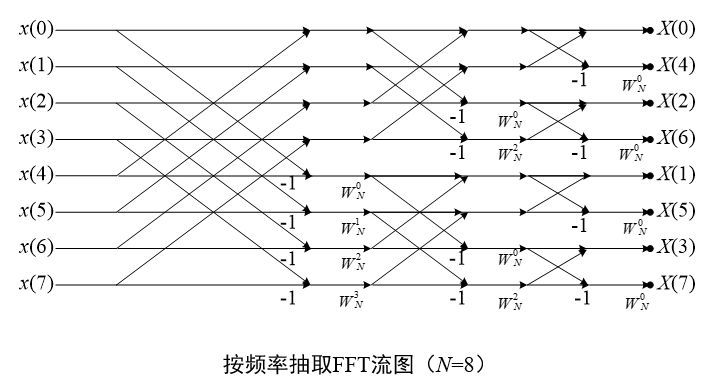
3. 運算量分析
通過前面的分析可見,兩種基2FFT算法,運算量是一樣的,N點DFT,就分解成了若干個蝶形的運算而已。
多少個蝶形呢?序列長度 N=2^M,共有 M級蝶形,每級N/2 個蝶形,共MN/2個。
而每個蝶形是1次復數乘法,2次復數加法。所以總的運算量為:

以N=1024=2^10為例,直接計算DFT,需要1024的平方=1048576
次乘法,而采用FFT只需要(1024/2)×10=5120次乘法,二者的比值為204.8。運算量減少了好幾個數量級。
頻率作為自然界的一個基本物理量,是很多領域研究的重要內容。人們很早就認識到,用DFT的方法可以有效進行信號的頻率分析。但是因為DFT算法運算量很大,在數字計算機發明以前,運算效率普遍很低的情況下,DFT也更多的是一種理論分析工具,很難被用于實際的信號處理。
FFT的出現,破解了這一歷史性難題,極大地促進了數字信號處理這門學科的應用和發展。有人甚至以FFT算法提出的1965年作為數字信號處理這門學科的誕生之年。
4. 算法特點
在計算機看來,這兩種算法是非常相像的。
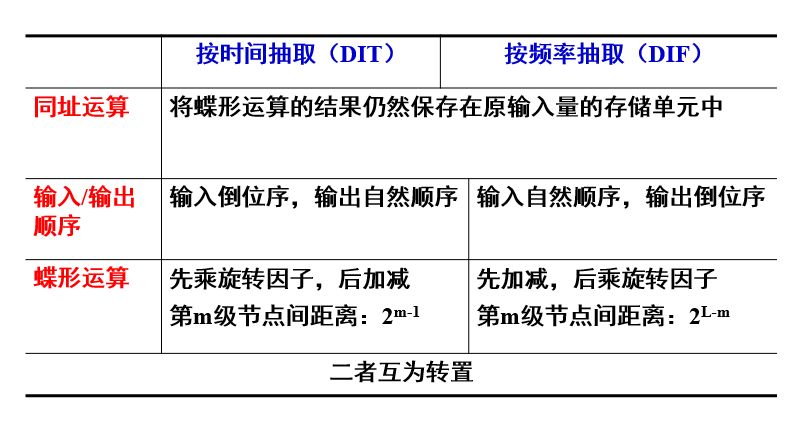
首先來看第一個特點:同址運算(又稱同位運算或原位運算),每完成一個蝶形運算,輸入的兩個數據就沒有用的,這就意味著,不需要再重新開辟新的存儲單元來保存輸出數據,計算結果仍保留在原輸入數據占據的存儲單元即可。
再來看第二個特點:輸入/輸出數據的順序。這是兩種算法的不同之處。以DIT-FFT為例來說明為什么會輸入倒位序。
還是以8點長數據為例,輸入數據的正常順序是x(0)、x(1)、x(2)......x(7),我們稱之為自然順序。按照序號的奇偶分為兩組,第一組是x(0)、x(2)、x(4)、x(6),第二組是x(1)、x(3)、x(5)、x(7)。每個新的組再重新排隊報數,按奇偶分,第一組又分成兩個組,分別是x(0)、x(4)和x(2)、x(6),第二組分成兩個組,分別是x(1)、x(5)和x(3)、x(7)。
也就是說,8點長序列的DIT-FFT,輸入數據的順序是:x(0)、x(4)、x(2)、x(6)、x(1)、x(5)、x(3)、x(7)。這個序號的順序乍看雜亂無章,其實有規律性。0、1、2、3、4、5、6、7的順序與0、4、2、6、1、3、5、7有何關系的呢?用二進制來寫一目了然,看下面的動圖:
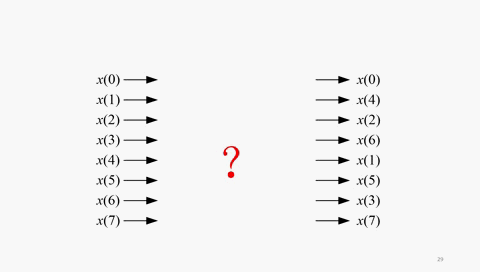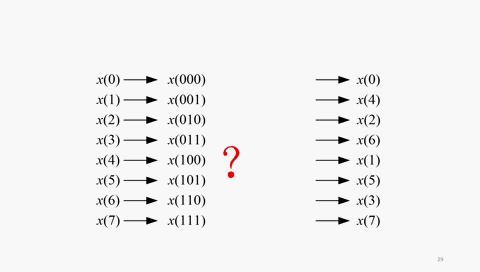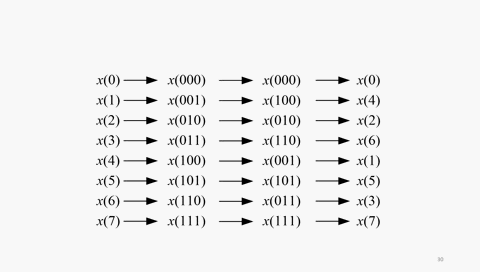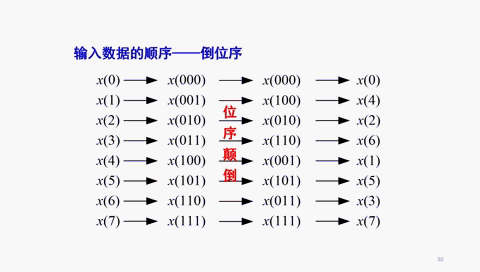
倒位序,是將二進制數的最高有效位到最低有效位的位序進行顛倒排列而得到的二進制數。
DIT-FFT算法中,對時域序列按照序號的奇偶進行分解,造成輸入序列的序號按照倒位序排列。
最后再說一說蝶形運算的規律。兩種FFT算法,最終都是轉換成了M列、每列N/2個、一共MN/2個蝶形運算。但二者蝶形運算的規律有差異。
第一個差異:基本蝶形不同。DIT是先乘旋轉因子,再加或減;而DIF是先加或減,再乘旋轉因子。
第二個差異:兩種算法,蝴蝶翅膀的距離(即節點間的距離)和旋轉因子的數目恰好相反。
仔細觀察兩種算法的流圖,我們會發現,二者互為轉置。
4.3其他FFT算法簡介
1. 混合基FFT

2. Chirp-z變換
實際應用中,有時只對信號的某一頻段感興趣,即只需要計算單位圓上某一段的頻譜值,而不需要計算[0,Π]區間的所有頻譜采樣值。此時,可以用”Chirp-z變換“(CZT)。
適用場合:窄帶信號的DFT。
3.Goertzel算法
在某些應用場合,只需計算很少幾個頻率點的頻譜值。例如,雙音多頻信號(DTMF)的檢測。此時可以采用卡澤爾(Goertzel)算法。
除此之外,傅里葉變換的快速算法還有很多種。不過應用最廣泛的依然能是基2FFT算法,它是數字信號處理最經典算法之一,幾乎各種主流的計算機編程語言都有現成的函數可以調用。不同型號的芯片,硬件開發商也都會給出優化后的FFT算法源代碼,一般情況下直接調用就可以。
-
DFT
+關注
關注
2文章
231瀏覽量
22757 -
序列
+關注
關注
0文章
70瀏覽量
19572 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42636
原文標題:數字信號處理系列串講第10篇(離散信號的頻域分析之四)——快速傅里葉變換FFT
文章出處:【微信號:SignalAndSystem_DSP,微信公眾號:信號與系統和數字信號處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 快速傅里葉變換FFT進行串講
快速傅里葉變換FFT進行串講
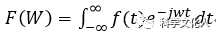










評論