前言
前兩篇文章介紹了PCA(主成分分析方法)和SVD(奇異值分解)的算法原理,本文基于scikit learn包介紹了PCA算法在降維和數據重構的應用,并分析了PCA類與sparsePCA類的區別。由于PCA算法的特征值分解是奇異值分解SVD的一個特例,因此sklearn工具的PCA庫是基于SVD實現的。
本文內容代碼鏈接:
https://github.com/zhangleiszu/machineLearning/tree/master/PCA
目錄
1. PCA類介紹
2. sklearn.decomposition.PCA的參數說明
3. sklearn.decomposition.MiniBatchSparsePCA的參數說明
4. PCA類在降維的應用
5. PCA類與MiniBatchSparsePCA類的區別
6. PCA在數據重構的應用
7. 總結
1. PCA類介紹
所有PCA類都在sklearn.decompostion包中,主要有以下幾類:
1) sklearn.decompostion.PCA:實際項目中用的最多的PCA類;
2) sklearn.decompostion.IncrementPCA:PCA最大的缺點是只支持批處理,也就是說所有數據都必須在主內存空間計算,IncrementalPCA使用多個batch,然后依次調用partial_fit函數,降維結果與PCA類基本一致 。
3) sklearn.decomposition.SparsePCA和sklearn.decomposition.MiniBatchSparsePCA:SparsePCA類和MiniBatchSparsePCA類算法原理一樣,都是把降維問題用轉換為回歸問題,并在優化參數時增加了正則化項(L1懲罰項),不同點是MiniBatchSparsePCA使用部分樣本特征并迭代設置的次數進行PCA降維 。
4) sklearn.decomposition.KernelPCA:對于線性不可分的特征,我們需要對特征進行核函數映射為高維空間,然后進行PCA降維 。流程圖如下:
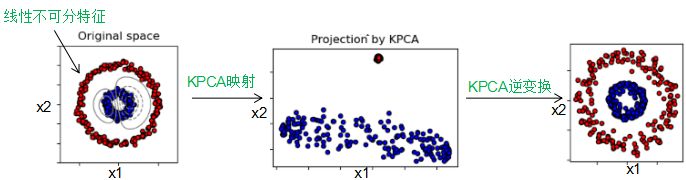
2. sklearn.decomposition.PCA類的參數說明
1) n_components:取值為:整形,浮點型,None或字符串。
n_components為空時,取樣本數和特征數的最小值:
n_components == min(n_samples , n_features)
0 < n_components < 1時,選擇主成分的方差和占總方差和的最小比例閾值,PCA類自動計算降維? ? ?后的維數。
n_components是大于等于1的整數,設置降維后的維數 。
n_components是字符串'mle',PCA類自動計算降維后的維數 。
2) copy:布爾型變量 。表示在運行時是否改變訓練數據,若為True,不改變訓練數據的值,運算結果寫在復制的訓練數據上;若為False,則覆蓋訓練數據 ,默認值為True。
3) whiten:布爾型變量 。若為True,表示對降維后的變量進行歸一化;若為False,則不進行歸一化 ,默認值為False。
4) svd_solver:字符串變量,取值為:'auto','full','arpack','randomized'
randomized:如果訓練數據大于500×500,降維后的維數小于數據的最小維數0.8倍,采用加快SVD的隨機算法 。
full:傳統意義上的SVD算法,調用scipy.linalg.svd類。
arpack:調用scipy.sparse.linalg.svds類,降維后的維數符合:
0 < n_components < min(X.shape)
auto:自動選擇最適合的SVD算法。
類成員屬性:
components_:主成分分量的向量空間 。
explained_variance_:向量空間對應的方差值 。
explained_variance_ratio_:向量空間的方差值占總方差值的百分比 。
singular_values:向量空間對應的奇異值 。
3.sklearn.decomposition.MiniBatchSparsePCA的參數說明
本節就介紹兩個常用的重要變量,用法與PCA類基本相同。
n_components:降維后的維數
alpha:正則化參數,值越高,主成分分量越稀疏(分量包含0的個數越多)。
4. PCA類在降維的應用
Iris數據集包含了三種花(Setosa,Versicolour和Virginica),特征個數為4。
下載Iris數據集:
iris = datasets.load_iris()X = iris.datay = iris.target
設置降維后的維數為2:
pca = PCA(n_components=2)
降維后的數據集:
X_r = pca.fit(X).transform(X)
降維后的特征分布圖:
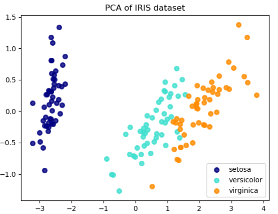
5. PCA類與MiniBatchSparsePCA類的區別
PCA類主成分分量是非零系數構成的,導致了PCA降維的解釋性很差,若主成分分量包含了很多零系數,那么主成分分量可以將很多非主要成分的影響降維0,不僅增強了降維的解釋性,也降低了噪聲的影響 ,缺點是可能丟失了訓練數據的重要信息。MiniBatchSparsePCA與PCA類的區別是使用了L1正則化項,導致了產生的主成分分量包含了多個0,L1正則化系數越大,0的個數越多,公式如下:
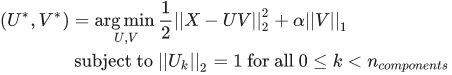
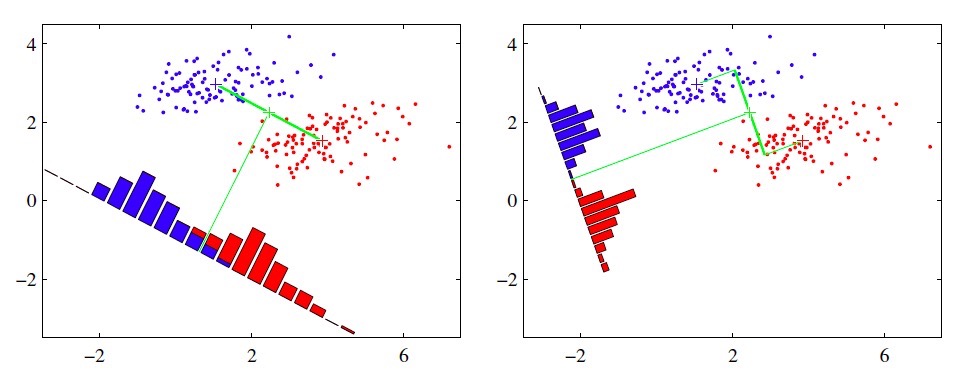
用圖來說明區別:
左圖是PCA類的主成分分量空間,右圖是MiniBatchSparsePCA類的主成分分量空間,比較兩圖可知,右圖能夠定位到重要的特征部位 。
若是用數值表示,MiniBatchSparsePCA類的主成分分量值為:

由上圖可知,主成分分量包含了很多零分量 。
6. PCA在數據重構的應用
數據重構算法借鑒上一篇文章的圖:
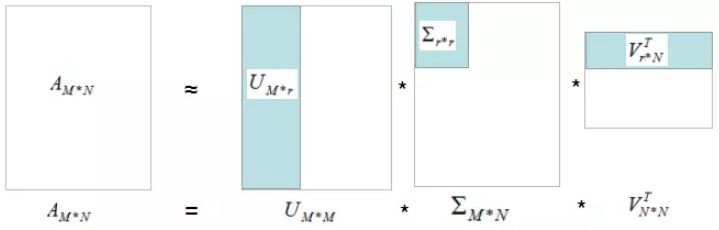
淺藍色部分矩陣的乘積為數據的重構過程,r為選擇的主成分分量個數 。r越大,重構的數據與原始數據越接近或主成分分量的方差和比例越大,重構的數據與原始數據越接近 ,圖形解釋如下:
n_components是0.2的數據重構圖:

n_components是0.9的數據重構圖:

因此,主成分分量越多,重構的數據與原始數據越接近。
7. 總結
本文介紹了PCA類在降維和數據重構的簡單用法以及分析了sparsePCA類稀疏主成分分量的原理。
-
函數
+關注
關注
3文章
4327瀏覽量
62573 -
數據集
+關注
關注
4文章
1208瀏覽量
24689 -
PCA算法
+關注
關注
0文章
2瀏覽量
1297
原文標題:scikit learn中PCA的使用方法
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦

FPGA的重構方式
求助,SVM分類時要不要先進行PCA降維呢?
【FPGA學習】VHDL的數據類型類預定義屬性和數據范圍類預定義屬性是怎么用的
可重構波束天線技術在增加網絡容量應用
為什么要重構?如何重組Python包?
基于Autoencoder網絡的數據降維和重構
java并發編程實戰之輔助類用法
Java數組的常用方法_Java:數組工具類Arrays類的常用方法的用法及代碼
融合尺度降維和重檢測的長期目標跟蹤算法

STM8L定時器1和定時器4的簡單用法





 PCA類在降維和數據重構的簡單用法
PCA類在降維和數據重構的簡單用法










評論