在信號(hào)分析與處理中,頻譜分析是重要的工具。FFT可以將時(shí)域信號(hào)轉(zhuǎn)換至頻域,以獲得信號(hào)的頻率結(jié)構(gòu)、幅度、相位等信息。該算法在理工科課程中都有介紹,眾多的儀器或軟件亦集成此功能。FFT實(shí)用且高效,相關(guān)原理與使用注意事項(xiàng)也值得好好學(xué)習(xí)。
01何為FFT
對(duì)于模擬信號(hào)的頻譜分析,首先得使用ADC(模擬數(shù)字轉(zhuǎn)換器)進(jìn)行采樣,轉(zhuǎn)換為有限序列x(n),其非零值長(zhǎng)度為N,經(jīng)DFT(離散傅立葉變換)即可轉(zhuǎn)化為頻域。DFT變換式為:
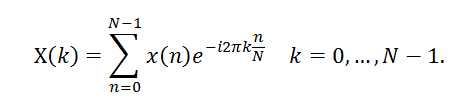
在上式中,N點(diǎn)序列的DFT需要進(jìn)行N2次復(fù)數(shù)乘法和N(N-1)次復(fù)數(shù)加法,運(yùn)算量大。FFT是DFT的快速算法,利用DFT運(yùn)算中的對(duì)稱性與周期性,將長(zhǎng)序列DFT分解為短序列DFT之和。最終運(yùn)算量明顯減少,使得FFT應(yīng)用更加廣泛。
1.1FFT基于的基本理論
FFT基于一個(gè)基本理論:任何連續(xù)的波形,都可以分解為不同頻率的正弦波形的疊加。FFT將采樣得到的原始信號(hào),轉(zhuǎn)化此信號(hào)所包含的正弦波信號(hào)的頻率、幅度、相位,為信號(hào)分析提供一個(gè)創(chuàng)新視覺(jué)。
例如在日常生活中有使用到的AM(AmplitudeModulation,幅度調(diào)制)廣播,其原理是將人的聲音(頻率約20Hz至20kHz,稱為調(diào)制波)調(diào)制到500kHz~1500kHz正弦波上(稱為載波)中 ,載波的幅度隨調(diào)制波的幅度變化。聲音經(jīng)這樣調(diào)制后,可以傳播得更遠(yuǎn)。在AM的時(shí)域波形(波形電壓隨時(shí)間的變化曲線),載波與調(diào)制波特征不易體現(xiàn),而在FFT后的幅頻曲線中則一目了然。如下圖為1000kHz載波、10kHz調(diào)制波的AM調(diào)制信號(hào),時(shí)域信號(hào)經(jīng)FFT后其頻率能量出現(xiàn)在990kHz、1.01MHz頻率處,符合理論計(jì)算。
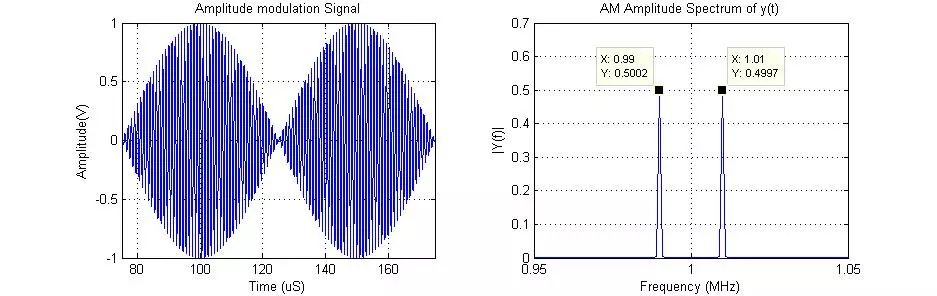
圖1 調(diào)制波10kHz、載波1000kHz的AM時(shí)域與頻域曲線
02FFT相關(guān)知識(shí)
現(xiàn)實(shí)生活中的模擬信號(hào),大多都是連續(xù)復(fù)雜的,其頻譜分量十分豐富。正如在數(shù)學(xué)中常量π,其真實(shí)值是個(gè)無(wú)理數(shù)。當(dāng)用3.14來(lái)替代π時(shí),計(jì)算值與真實(shí)值就會(huì)有偏差。在使用FFT這個(gè)工具時(shí),受限于采樣時(shí)的頻率Fs、采樣點(diǎn)長(zhǎng)度N、ADC的分辨率nbit等因素的制約,所得到的信息會(huì)有所缺失與混淆。
2.1奈奎斯特區(qū)與波形混疊
FFT分析結(jié)果中,存在一個(gè)那奈奎斯特區(qū)的概念,其寬度為采樣率的一半Fs/2,信號(hào)頻譜被分成一個(gè)個(gè)相連的奈奎斯特區(qū)。日常信號(hào)分析中,大多關(guān)心的是1st奈奎斯特區(qū)的信號(hào),即DC到Fs/2的頻段。FFT所得到的信號(hào)頻率信息,也是在1st奈奎斯特區(qū)內(nèi)。其他高奈奎斯特區(qū)頻段的信號(hào),會(huì)以不同的方式混疊到1st奈奎斯特區(qū):
偶數(shù)奈奎斯特區(qū)會(huì)鏡像后混疊到1st奈奎斯特區(qū);
奇數(shù)奈奎斯特區(qū)會(huì)頻移后混疊到1st奈奎斯特區(qū)。
如下圖所示,假如原有模擬信號(hào)頻譜段較寬,信號(hào)頻段的最大頻率大于采樣率Fs。在采樣率Fs下,信號(hào)頻譜的A、B、C三部分區(qū)域,分別位于1st、2st、3st奈奎斯特區(qū)。那經(jīng)FFT后:
A部分信號(hào)本來(lái)就在1st奈奎斯特區(qū),保持不變;
B部分頻譜會(huì)以Fs/2為鏡像后混疊到1st奈奎斯特區(qū);
C部分頻譜頻偏Fs后混疊到1st奈奎斯特區(qū)。
這樣在FFT的分析結(jié)果中,1st奈奎斯特區(qū)就會(huì)重疊了A、B、C三部分區(qū)域的信號(hào)。其他奈奎斯特區(qū)頻率信號(hào)干擾到需分析的信號(hào),就會(huì)造成常說(shuō)的波形混疊問(wèn)題。
就單個(gè)頻率信號(hào)而言,若原始信號(hào)的頻率為|±KFs ±Fin|(K為自然數(shù)),則經(jīng)過(guò)FFT分析后,信號(hào)會(huì)落入在1st奈奎斯特區(qū)的Fin頻率處。
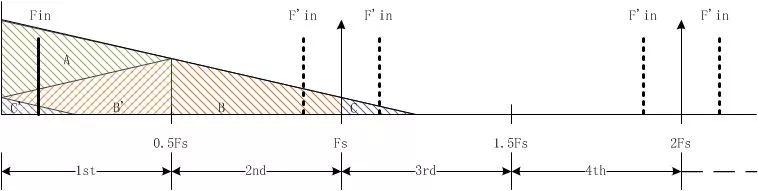
圖2 奈奎斯特區(qū)投影與波形混疊
這在時(shí)域上理解不難:在常用設(shè)備示波器的采樣率設(shè)為100MSa/s,這時(shí)輸入10MHz、90MHz、110MHz頻率的信號(hào),采樣得到的波形是一樣的,都為10MHz。此時(shí)奈奎斯特區(qū)寬度為50MHz,信號(hào)90MHz位于2st奈奎斯特區(qū),經(jīng)Fs/s鏡像后,為10MHz;信號(hào)110MHz位于3st奈奎斯特區(qū),經(jīng)頻偏Fs后,亦為10MHz。在FFT后的數(shù)據(jù)中,這三個(gè)頻率信號(hào)的頻點(diǎn)都落在1st奈奎斯特區(qū)的10MHz處。
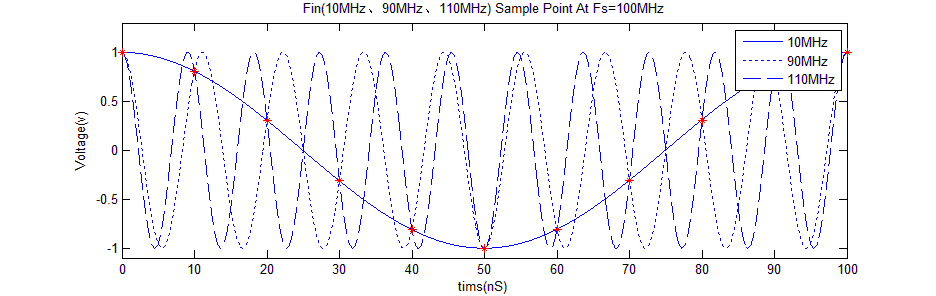
圖3 波形混疊時(shí)的時(shí)域芯片
為了解決信號(hào)混疊問(wèn)題,可以采取以下措施:
提高模數(shù)轉(zhuǎn)換器ADC的采樣率Fs
這相當(dāng)把1st奈奎斯特區(qū)拉寬。當(dāng)滿足Fs/2大于信號(hào)頻段的最大頻率Fin_max時(shí),自然不會(huì)現(xiàn)混疊。這是采樣定理的簡(jiǎn)單實(shí)踐。
在模數(shù)轉(zhuǎn)換器前串入抗混疊濾波器
抗混疊濾波器最常見(jiàn)的是低通濾波器,此濾波器可以將高于Fs/2的高階奈奎斯特區(qū)頻段信號(hào)衰減掉,只保留待測(cè)量1st奈奎斯特區(qū)頻段的信號(hào)。
2.2FFT數(shù)據(jù)的物理意義
長(zhǎng)度為N的有限序列x(n),經(jīng)FFT后得會(huì)到N個(gè)復(fù)數(shù),完成了時(shí)域到頻域的涅磐。原始信號(hào)包含的各種正弦信號(hào),會(huì)轉(zhuǎn)化成對(duì)應(yīng)位置的復(fù)數(shù):
第一個(gè)復(fù)數(shù),代表信號(hào)的直流分量。此復(fù)數(shù)的模值,為直流分量的N倍。
第二至第N/2個(gè)復(fù)數(shù),代表著均勻頻率間隔信號(hào)的特征。此復(fù)數(shù)的模,為此頻率信號(hào)幅度的N/2倍;此復(fù)數(shù)的角度,為此頻率信號(hào)的相位。一個(gè)奈奎斯特區(qū)包含N/2個(gè)頻率點(diǎn),頻率點(diǎn)的間隔稱為頻率分辨率:
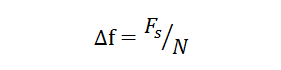
對(duì)上式稍作變換:頻率分辨率的倒數(shù),為可分析信號(hào)的周期:
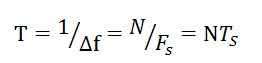
NTs即采樣時(shí)間,可見(jiàn)FFT的頻率分辨率,與其他參數(shù)無(wú)關(guān),只與采樣時(shí)間長(zhǎng)度有關(guān)。
第N/2+1至第N個(gè)復(fù)數(shù),從上文的奈奎斯特區(qū)可知,是1st奈奎斯特區(qū)的鏡像,可以忽略。
2.3頻譜泄漏與窗函數(shù)
在利用FFT對(duì)ADC的動(dòng)態(tài)性能評(píng)估中,為了減少不相關(guān)因素對(duì)動(dòng)態(tài)性能的影響,測(cè)試中一般要求給ADC低噪電源、低噪時(shí)鐘,待測(cè)信號(hào)幅度盡量接近且略低于ADC的輸入量程,而待測(cè)信號(hào)的頻率Fin也有要求:
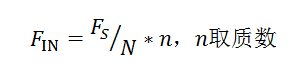
為啥頻率要這樣要求?
將上式中的頻率轉(zhuǎn)換為周期就很好理解:
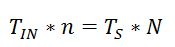
TS*N即為采樣時(shí)間,采樣時(shí)間剛好包含了n個(gè)整周期的待測(cè)信號(hào)。這樣選取輸入信號(hào)頻率的原因,是FFT分析中默認(rèn)采集到的數(shù)據(jù),是原始連續(xù)波形中的一段周期波形。既然波形是連續(xù)的,那波形肯定首尾相連的、開(kāi)始點(diǎn)電壓值等于終點(diǎn)處電壓值的。
若采樣到的數(shù)據(jù)不是連續(xù)的,則相當(dāng)數(shù)據(jù)在首尾處有一個(gè)電壓突變,電壓突變?cè)陬l域上就代表著很高的頻率分量。這些高頻的頻率分量混疊到1st奈奎斯特區(qū)時(shí),就會(huì)對(duì)原有信號(hào)的頻譜造成干擾,這也叫頻譜泄漏。
在實(shí)際的信號(hào)分析中,待測(cè)信號(hào)的頻率是很難事先設(shè)定的,這就容易會(huì)造成頻譜泄漏。為了減輕這個(gè)影響,F(xiàn)FT加入了窗函數(shù)這個(gè)概念。窗函數(shù),其實(shí)是一個(gè)加權(quán)系數(shù),將不同位置的采樣點(diǎn),分別乘以不同的系數(shù)。經(jīng)過(guò)加權(quán)相乘后,采樣點(diǎn)就變成首尾相連的連續(xù)波形了。不同的窗函數(shù),其加權(quán)曲線不一樣,造成的影響就有所差異。舉例hann窗的系數(shù)定義如下:
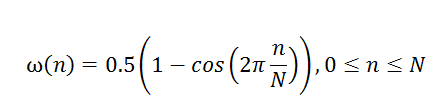
其N=64系數(shù)曲線與頻譜如下:
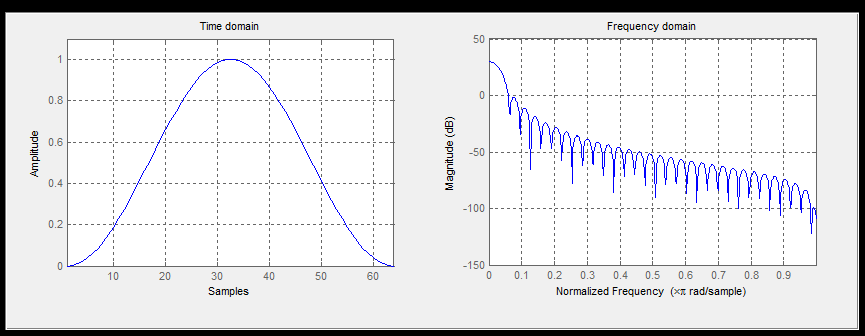
圖4 N=64 hann窗系數(shù)曲線與頻譜曲線
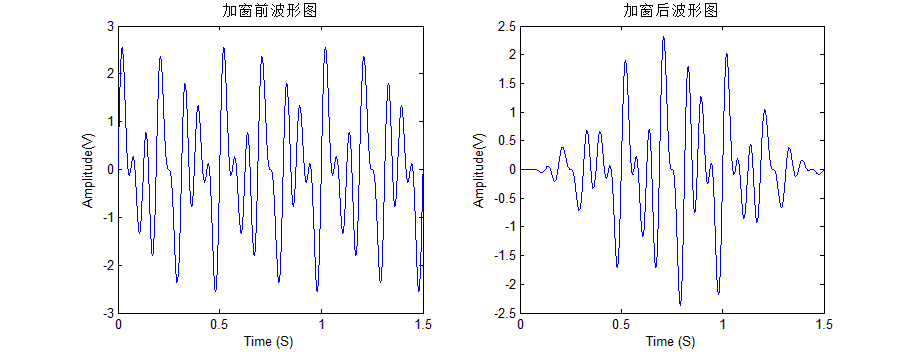
圖5 疊加窗前后的信號(hào)波形
2.41頻譜圖指標(biāo)定義
將FFT得到的各個(gè)頻率點(diǎn)幅度,繪制成隨頻率變化的曲線,可以得到信號(hào)的頻譜圖。在原廠ADC的器件手冊(cè)或性能評(píng)估方案中,會(huì)有與性能相關(guān)指標(biāo)的定義。在眾多指標(biāo)中,以下幾個(gè)尤為重要:
信噪比SNR
信號(hào)均方根幅值與除前六個(gè)諧波與直流分量之外的所有頻率分量均方根和之比。在只考慮ADC的量化誤差時(shí),SNR只與ADC的位數(shù)相關(guān)。
信納比SINAD
信號(hào)均方根振幅與出直流分量之外的所有頻譜分量均方根和之比。SINAD與SNR之間的差異只有前六個(gè)諧波分量所含的能量。
總諧波失真THD
信號(hào)均方根與前六個(gè)諧波之和的均方根值之比。諧波的產(chǎn)生是因?yàn)樾盘?hào)經(jīng)過(guò)了非線性環(huán)節(jié),導(dǎo)致信號(hào)產(chǎn)生畸變。
無(wú)雜散動(dòng)態(tài)范圍SFDR
信號(hào)均方根與最大雜散頻譜分量均方根值之比。SFDR可以表征信號(hào)分析的動(dòng)態(tài)范圍。
有效位數(shù)ENOB
ENOB反映了信號(hào)與正弦波的擬合程度。在FFT中可以使用公式計(jì)算:ENOB =(SINAD-1.76)/6.02。這公式是與基于ADC只有量化誤差時(shí)的計(jì)算模型,具體的推論可以參考ADI的應(yīng)用文檔MT-001《Taking the Mystery out of the Infamous Formula,"SNR = 6.02N + 1.76dB," and Why You Should Care》。
圖6 ZDS4054 Plus FFT功能分析界面
ZDS4000 FFT分析功能可以自動(dòng)計(jì)算總諧波失真THD、信噪比SNR,顯示前10次高功率信號(hào)頻率。
03小結(jié)
FFT是簡(jiǎn)便而高效的分析工具,在眾多的軟件中都已很好的集成。在網(wǎng)絡(luò)上簡(jiǎn)單搜索一下例程,在Matlab軟件中簡(jiǎn)單敲入fft(),即可做信號(hào)分析。而致遠(yuǎn)電子推出的高性能數(shù)據(jù)挖掘性示波器,F(xiàn)FT分析的樣本數(shù)可達(dá)4Mpts,這使得示波器可以在最高采樣率下,采樣更長(zhǎng)時(shí)間的波形。這樣在FFT后,數(shù)據(jù)的奈奎斯特區(qū)就相當(dāng)寬,而頻率分辨率又相當(dāng)窄,非常適用信號(hào)分析與噪聲定位。
-
濾波器
+關(guān)注
關(guān)注
161文章
7805瀏覽量
178060 -
FFT
+關(guān)注
關(guān)注
15文章
434瀏覽量
59373 -
正弦波信號(hào)
+關(guān)注
關(guān)注
0文章
27瀏覽量
8270
原文標(biāo)題:千萬(wàn)別錯(cuò)過(guò)!這些FFT干貨真的很受用
文章出處:【微信號(hào):ZLG_zhiyuan,微信公眾號(hào):ZLG致遠(yuǎn)電子】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
膽機(jī)使用的注意事項(xiàng)
電池組的設(shè)計(jì)加工注意事項(xiàng)
鉭電解應(yīng)用注意事項(xiàng)
淺談PCB板設(shè)計(jì)注意事項(xiàng)
Protel布線設(shè)計(jì)注意事項(xiàng)
掌握液壓缸的特點(diǎn)及相關(guān)應(yīng)用與注意事項(xiàng)
輕負(fù)載時(shí)開(kāi)關(guān)元件工作相關(guān)的注意事項(xiàng)
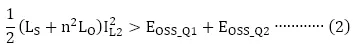
重負(fù)載時(shí)中開(kāi)關(guān)元件工作相關(guān)的注意事項(xiàng)




 FFT實(shí)用且高效,相關(guān)原理與使用注意事項(xiàng)
FFT實(shí)用且高效,相關(guān)原理與使用注意事項(xiàng)











評(píng)論