在推薦系統的相關研究中,我們常常用到兩個相關概念:矩陣分解和奇異值分解。這兩個概念是同一種算法嗎?兩者到底有什么差別?在本文中,作者梳理了兩種算法的概念、來源和內容,并進行了比較。通過對相關內容的梳理,作者提出,矩陣分解是推薦系統中最初使用的概念,奇異值分解是對該方法的進一步發展。在現在的討論中,一般將兩種方法統一成為奇異值分解。
在 Andrew Ng 教授的機器學習課程中,介紹推薦系統時經常涉及矩陣分解、奇異值分解等數學知識,這些概念并不是很好理解。在 Andrew Ng 教授的課程提到了一種稱為稱為 (低因子) 矩陣分解的方法,而在 Google 搜索會得到另一個名稱:奇異值分解。網絡資源中對于該算法的解釋和 Andrew Ng 教授存在差異,但很多人都認為這兩個名稱指的是同一種算法。為了更好的梳理這兩個概念,在本文中,我對兩者進行了分別介紹,并對比了它們的不同。
推薦系統
推薦系統 (Recommender Systems, RS) 是一種自動化的針對用戶的內容推薦方式,被廣泛用于電子商務公司,流媒體服務 (streaming services) 和新聞網站等系統。根據用戶的喜好,推薦系統能夠投其所好,為用戶推薦一些合適的內容,以便減少用戶篩選過程中一些不必要的麻煩。
推薦系統并不是一種全新的技術,相關概念最晚在1990年就出現了。事實上,當前的機器學習熱潮,一部分要歸因于人們對 RS 的廣泛關注。 在2006年,Netflix 贊助了一場為電影尋找最佳推薦系統的競賽,在當時引起了一片轟動,也讓推薦系統再次得到了廣泛的關注。
矩陣表示
我們可以有很多種方式來向別人推薦一部電影。其中一種效果較好的策略,是將用戶對電影的評分看做一個用戶 x 電影矩陣,如下所示:
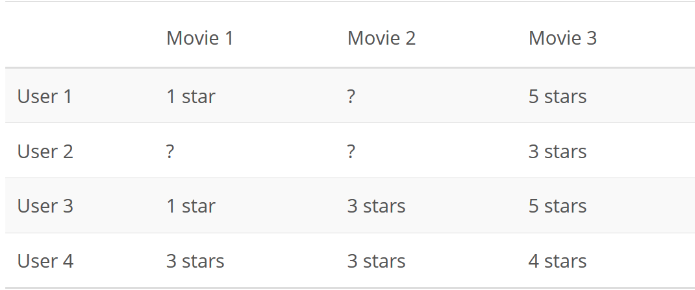
在該矩陣中,問號代表用戶未評分的電影。隨后,只需要以某種方式預測來用戶對電影評分,并向用戶推薦他們可能喜歡的電影。
矩陣分解
在 Netflix 舉辦的比賽上,參賽者 Simon Funk 提出了一個很好的想法,即用戶對電影的評分不是隨給出的。用戶會基于一定的邏輯,針對電影中他所所喜歡的部分 (如特定的女演員或類型) 和不喜歡的情節 (長時間或糟糕的笑話) 賦予不同的權重,并進行加權計算,最后得到一個分數作為該電影的評分。這個過程可以用如下公式表示:
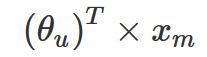
其中 xm 是電影 m 特征值的一個列向量,而 θ? 是另一個列向量,表示用戶 u 賦予每個電影特征的權重。每個用戶都有不同的權重集合,而每個電影的特征也對應不同的特征集合。
事實證明,如果能夠任意地修改特征的數量并忽略所缺失的那部分電影評分,那么就可以找到一組權重和特征值,依據這些值所創建新矩陣與原始的評分矩陣是很接近的。這一過程可以通過梯度下降來實現,且類似于線性回歸中所使用的梯度下降,只不過我們需要同時優化權重和特征這兩組參數。以上文提供的用戶-電影矩陣為例,優化后得到的結果將生成如下新的矩陣:
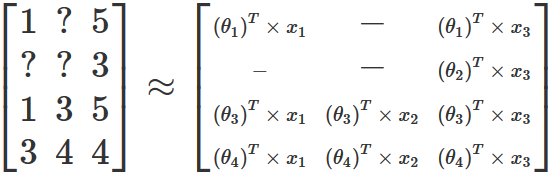
值得注意的是,在大多數真實數據集中,生成的結果矩陣并不會精確地與原始矩陣保持一致。因為在現實生活中,用戶不會對通過矩陣乘法和求和等操作對電影進行評分。大多數情況下,用戶對電影進行評分只是一種主觀性的行為,且可能受到各種外部因素的影響。盡管如此,這里所介紹的方法還是希望通過數學公式來表達用戶在電影評分時的主要邏輯。
通過上面的計算,現在我們已經得到了一個近似矩陣,那該如何來預測缺失的電影評級呢?通過回顧上面的計算過程,我們可以發現,為了構建這個新矩陣,這里定義了一個公式來填充矩陣中的所有值,包括原始矩陣中的缺失值。因此,如果想要預測缺失的用戶電影評分,這里只需獲取該缺失電影的所有特征值,再乘以該用戶的所有權重并將所有內容相加,就能得到用戶對該電影的評分。因此在這里,如果想要預測用戶2對電影1的評級,可以通過以下計算:
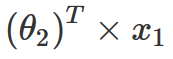 ? ? ?
? ? ?
為了簡化表達式,在這里可以對 θ 和 x 進行分離,并將它們放入各自的矩陣(比如 P 和 Q)。
以上就是 Funk 所提出的矩陣分解方法,也是 Andrew Ng 教授在課上所提到的矩陣分解。該方法在當時 Netflix 競賽中獲得第三名,引起了廣泛的關注,并在當前許多應用中仍被使用。
奇異值分解
下面介紹奇異值分解 (Singular Value Decomposition, SVD)。SVD 方法是將一個矩陣分解為三個矩陣的矩陣分解方法,即 A =UΣV?,且三個分解矩陣會具有一些較好的數學特性。
SVD 方法具有廣泛的應用,其中之一就是主成分分析(Principal Component Analysis, PCA) ,該方法能夠將維度 n 的數據集減少到 k 個維度 (k
這里不再展開介紹 SVD 方法的詳細信息。我們只需要記住,奇異值分解與矩陣分解的處理方式不同。使用SVD 方法會得到三個分解矩陣,而 Funk 提出的矩陣分解方式只創建了兩個矩陣。
那為什么在每次搜索推薦系統時總會彈出 SVD 的相關內容呢? Luis Argerich 認為原因在于:
事實上,矩陣分解是推薦系統中首先使用的方法,而 SVD++ 可視為是對它的一種擴展形式。正如 Xavier Amatriain 所說的那樣:
而 Wikipedia 在對矩陣分解(推薦系統)的相關條目中也有類似的表述:
最后,簡單進行一下總結:
奇異值分解(SVD)是一種相對復雜的數學技術,它將矩陣分解為三個新的矩陣,并廣泛應用于當前許多的應用中,包括主成分分析(PCA)和推薦系統(RS)。
Simon Funk 在2006年的 Netflix 競賽中提出并使用了一個非常好的策略,改方法將矩陣分解為兩個權重矩陣,并使用梯度下降來找到特征和權重所對應的的最優值。實質上,這是不同于 SVD 方法的另一種技術,將其稱為矩陣分解更為合適。
隨著這兩種方法的廣泛應用,研究者并沒有嚴謹地在術語上區分這兩種方法,而是統一將其稱為 SVD。


-
矩陣
+關注
關注
0文章
423瀏覽量
34528 -
機器學習
+關注
關注
66文章
8406瀏覽量
132566 -
奇異值分解
+關注
關注
0文章
4瀏覽量
6362
原文標題:一文幫你梳理清楚:奇異值分解和矩陣分解 | 技術頭條
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
MATLAB線性方程和特征值和奇異值命令
工業互聯網和工業4.0傻傻分不清楚?
不要再對各種電機、舵機傻傻分不清楚了 精選資料分享
基于改進奇異值分解的人耳識別算法研究
采用奇異值分解的數字水印嵌入算法
基于整體與部分奇異值分解的人臉識別
基于奇異值分解的車牌特征提取方法研究
基于矩陣分解的手機APP推薦
芯片、半導體、集成電路還在傻傻分不清楚
基于奇異值分解的時空序列分解模型ST-SVD





 奇異值分解和矩陣分解傻傻分不清楚?一文幫你理清兩者差異!
奇異值分解和矩陣分解傻傻分不清楚?一文幫你理清兩者差異!










評論