【導語】本文對梯度函數和損失函數間的關系進行了介紹，并通過可視化方式進行了詳細展示。另外，作者對三種常見的損失函數和兩種常用的激活函數也進行了介紹和可視化。

你需要掌握關于神經網絡訓練的基礎知識。本文嘗試通過可視化方法，對損失函數、梯度下降和反向傳播之間的關系進行介紹。

損失函數和梯度下降之間的關系

為了對梯度下降過程進行可視化，我們先來看一個簡單的情況：假設神經網絡的最后一個節點輸出一個權重數w，該網絡的目標值是0。在這種情況下，網絡所使用的損失函數為均方誤差（MSE）。

當w大于0時，MSE的導數 dy/dw 值為正。dy/dw 為正的原因可以解釋為，w中的正方向變化將導致y的正方向變化。為了減少損失值，需要在w的負方向上進行如下變換：

當w小于0時，MSE的導數 dy/dw 值為負，這意味著w中的正方向變化將導致y的負方向變化。 為了減少損失，需要在w的正方向上做如下變換：

因此，權重更新的公式如下：

其中 learning_rate 是一個常量，用于調節每次更新的導數的百分比。調整 Learning_rate 值主要是用于防止w更新步伐太小或太大，或者避免梯度爆炸（梯度太大）或梯度消失的問題（梯度太小）。

下圖展示了一個更長且更貼近實際的計算過程，在該計算過程中，需要使用sigmoid激活函數對權重進行處理。為了更新權重w1，相對于w1的損失函數的導數可以以如下的方式得到：

損失函數對權重的求導過程

從上面闡釋的步驟可以看出，神經網絡中的權重由損失函數的導數而不是損失函數本身來進行更新或反向傳播。因此，損失函數本身對反向傳播并沒有影響。下面對各類損失函數進行了展示：

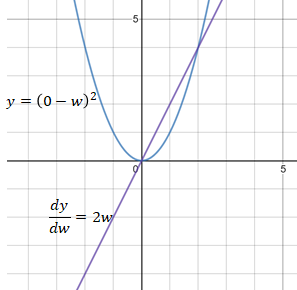
L2損失函數

MSE（L2損失）的導數更新的步長幅度為2w。 當w遠離目標值0時，MSE導數的步長幅度變化有助于向w反向傳播更大的步長，當w更接近目標值0時，該變化使得向w進行反向傳播的步長變小。

L1損失函數

MAE（L1損失）的導數是值為1或負1的常數，這可能不是理想的區分w與目標值之間距離的方式。

交叉熵損失函數

交叉熵損失函數中w的范圍是0和1之間。當w接近1時，交叉熵減少到0。交叉熵的導數是 -1/w。

Sigmoid激活函數

Sigmoid函數的導數值域范圍在0到0.25之間。 sigmoid函數導數的多個乘積可能會得到一個接近于0的非常小的數字，這會使反向傳播失效。這類問題常被稱為梯度消失。

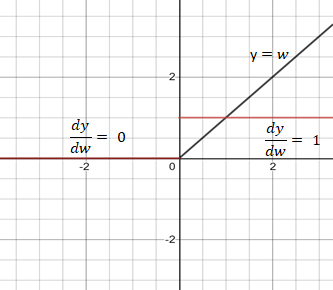
Relu激活函數

Relu是一個較好的激活函數，其導數為1或0，在反向傳播中使網絡持續更新權重或不對權重進行更新。