【導(dǎo)語】本文對傳統(tǒng)的人工數(shù)學(xué)建模和機器學(xué)習(xí)的優(yōu)缺點進行了介紹和比較，并介紹了一種將二者優(yōu)點相結(jié)合的方法——解耦表示學(xué)習(xí)。之后，作者利用 DeepMind 發(fā)布的基于解耦表示學(xué)習(xí)的 beta-VAE 模型，對醫(yī)療和金融領(lǐng)域的兩個數(shù)據(jù)集進行了探索，展示了模型效果，并提供了實驗代碼。

這篇文章會對傳統(tǒng)數(shù)學(xué)建模與機器學(xué)習(xí)建模之間的聯(lián)系進行討論。傳統(tǒng)數(shù)學(xué)建模是我們在學(xué)校里都學(xué)過的建模方法，該方法中，數(shù)學(xué)家們基于專家經(jīng)驗和對現(xiàn)實世界的理解進行建模。而機器學(xué)習(xí)建模則是另一種完全不同的建模方式，機器學(xué)習(xí)算法以一種更加隱蔽的方式來描述一些客觀事實，盡管人類并不能夠完全理解模型的描述過程，但在大多數(shù)情況下，機器學(xué)習(xí)模型要比人類專家構(gòu)建的數(shù)學(xué)模型更加精確。當(dāng)然，在更多應(yīng)用領(lǐng)域（如醫(yī)療、金融、軍事等），機器學(xué)習(xí)算法，尤其是深度學(xué)習(xí)模型并不能滿足我們需要清晰且易于理解的決策。

本文會著重討論傳統(tǒng)數(shù)學(xué)建模和機器學(xué)習(xí)建模的優(yōu)缺點，并介紹一個將兩者相結(jié)合的方法 —— 解耦表示學(xué)習(xí) (Disentangled Representation Learning)。

如果想在自己的數(shù)據(jù)集上嘗試使用解耦表示學(xué)習(xí)的方法，可以參考 Github 上關(guān)于解耦學(xué)習(xí)的分享，以及 Google Research 提供的關(guān)于解耦學(xué)習(xí)的項目代碼。

深度學(xué)習(xí)存在的問題

由于深度學(xué)習(xí)技術(shù)的發(fā)展，我們在許多領(lǐng)域都對神經(jīng)網(wǎng)絡(luò)的應(yīng)用進行了嘗試。在一些重要的領(lǐng)域，使用神經(jīng)網(wǎng)絡(luò)確實是合理的，并且獲得了較好的應(yīng)用效果，包括計算機視覺、自然語言處理、語音分析和信號處理等。在上述應(yīng)用中，深度學(xué)習(xí)方法都是利用使用線性和非線性轉(zhuǎn)換對復(fù)雜的數(shù)據(jù)進行自動特征抽取，并將特征表示為“向量”（vector），這一過程一般也稱為“嵌入”（embedding）。之后，神經(jīng)網(wǎng)絡(luò)對這些向量進行運算，并完成相應(yīng)的分類或回歸任務(wù)：

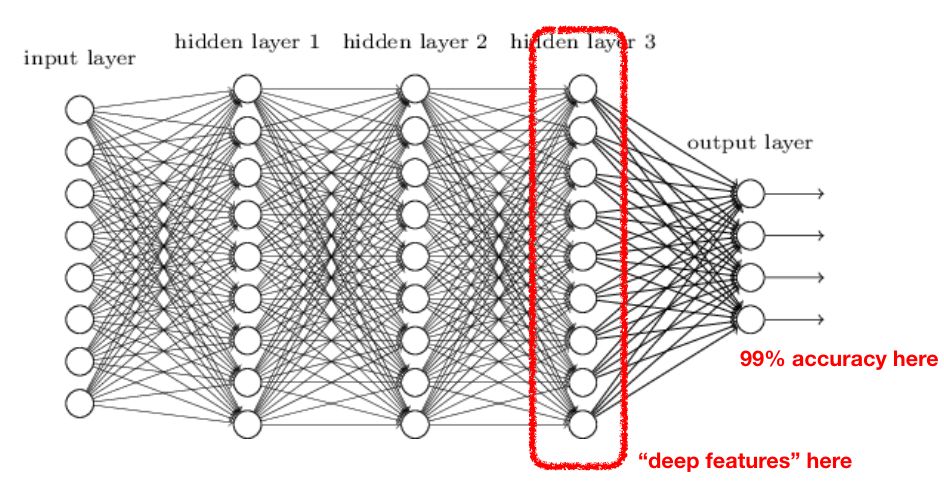
從特征提取和準(zhǔn)確度來看，這種 “嵌入”的方法非常有效，但在許多方面也存在不足：

可解釋性：嵌入所使用的N維向量無法對模型分析的原理和過程進行很好的解釋，只有通過逆向工程才能找到輸入數(shù)據(jù)中對分析影響更大的內(nèi)容。

數(shù)據(jù)需求量龐大：如果只有 10~100 個樣本，深度學(xué)習(xí)無法使用。

無監(jiān)督學(xué)習(xí)：大多數(shù)深度學(xué)習(xí)模型都需要有標(biāo)簽的訓(xùn)練數(shù)據(jù)。

零樣本學(xué)習(xí)：這是一個很關(guān)鍵的問題，基于一個數(shù)據(jù)集所訓(xùn)練出的神經(jīng)網(wǎng)絡(luò)，若不經(jīng)過重新訓(xùn)練，很難直接應(yīng)用在另一個數(shù)據(jù)集上。

對象生成：除了 GANs（生成對抗網(wǎng)絡(luò)）以外，其他模型都很難生成一個真實的對象。

對象操作：難以通過嵌入調(diào)整輸入對象的具體屬性。

理論基礎(chǔ)：雖然我們已經(jīng)掌握了比較通用的逼近理論，但這還不夠。

這些問題很難用機器學(xué)習(xí)框架來解決，但在最近，我們?nèi)〉昧艘恍┬碌倪M展。

數(shù)學(xué)建模的優(yōu)勢

在 20 年、50 年 甚至 100 年以前，大多數(shù)數(shù)學(xué)家都沒有遇到過上述問題。其中原因在于，他們主要關(guān)注數(shù)學(xué)建模（mathematical modeling），并通過數(shù)學(xué)抽象來描述現(xiàn)實世界中的對象和過程，如使用分布、公式和各種各樣的方程式。在這個過程中，數(shù)學(xué)家定義了我們在標(biāo)題中提到的常微分方程（ordinary differential equations, ODE）。我們通過對比深度學(xué)習(xí)存在的問題，對數(shù)學(xué)建模的特點進行了分析。需要注意的是，在下面的分析中，“嵌入”代表數(shù)學(xué)模型的參數(shù)，如微分方程的自由度集合。

可解釋性：每個數(shù)學(xué)模型都是基于科學(xué)家對客觀事物的描述而建立的，建模過程包含數(shù)據(jù)家對客觀事物的描述動機和深入理解。例如，對于物理運動的描述， “嵌入” 包括物體質(zhì)量、運動速率和坐標(biāo)空間，不涉及到抽象的向量。

數(shù)據(jù)需求量大：大多數(shù)數(shù)學(xué)建模上的突破并不需要基于巨大的數(shù)據(jù)集進行。

無監(jiān)督學(xué)習(xí)：對數(shù)學(xué)建模來說也不適用。

零樣本學(xué)習(xí)：一些隨機微分方程（如幾何布朗運動）可以應(yīng)用于金融、生物或物理領(lǐng)域，只需要對參數(shù)進行重新命名。

對象生成：不受限制，對參進行采樣即可。

對象操作：不受限制，對參數(shù)進行操作即可。

理論基礎(chǔ)：上百年的科學(xué)基礎(chǔ)。

我們沒有使用微分方程解決所有問題的原因在于，對于大規(guī)模的復(fù)雜數(shù)據(jù)來說，微分方程的表現(xiàn)與深度學(xué)習(xí)模型相比要差得多，這也是深度學(xué)習(xí)得到飛速發(fā)展的原因。但是，我們?nèi)匀恍枰斯さ臄?shù)學(xué)建模。

將機器學(xué)習(xí)與基于人工的建模方法相結(jié)合

如果在處理復(fù)雜數(shù)據(jù)時，我們能把表現(xiàn)較好的神經(jīng)網(wǎng)絡(luò)和人工建模方法結(jié)合起來，可解釋性、生成和操作對象的能力、無監(jiān)督特征學(xué)習(xí)和零樣本學(xué)習(xí)的問題，都可以在一定程度上得到解決。舉個例子，視頻1中呈現(xiàn)的是對于人像的特征提取方法。

對于微分方程和其他人工建模方法來說，圖像處理很難進行，但通過和深度學(xué)習(xí)進行結(jié)合，上述模型允許我們進行對象的生成和操作、可解釋性強，最重要的是，該模型可以在其他數(shù)據(jù)集上完成相同的工作。該模型唯一的問題是，建模過程不是完全無監(jiān)督的。另外，對于對象的操作還有一個重要的改進，即當(dāng)我改變 ”胡須“ 這一特征時，程序自動讓整張臉變得更像男人了，也就是意味著，模型中的特征雖然具有可解釋性，但特征之間是相關(guān)聯(lián)的，換句話說，這些特征是耦合在一起的。

β -VAE

有一個方法可以幫助我們實現(xiàn)解耦表示，也就是讓嵌入中的每個元素對應(yīng)一個單獨的影響因素，并能夠?qū)⒃撉度胗糜诜诸悺⑸珊土銟颖緦W(xué)習(xí)。該算法是由 DeepMind 實驗室基于變分自編碼器開發(fā)的，相比于重構(gòu)損失函數(shù)（restoration loss），該算法更加注重潛在分布與先驗分布之間的相對熵。

若想了解更多細節(jié)，可閱讀beta-VAE的論文（https://openreview.net/forum?id=Sy2fzU9gl）；也可參考這個視頻2中的介紹，詳細解釋了 beta-VAE 的內(nèi)在思想，以及該算法在監(jiān)督學(xué)習(xí)和強化學(xué)習(xí)中的應(yīng)用。

beta-VAE 可以從輸入數(shù)據(jù)中提取影響變量的因素，提取的因素包括物理運動的方向、對象的大小、顏色和方位等等。在強化學(xué)習(xí)應(yīng)用中，該模型可以區(qū)分目標(biāo)和背景，并能夠基于已有的訓(xùn)練模型在實際環(huán)境中進行零樣本學(xué)習(xí)。

實驗過程

我主要研究醫(yī)療和金融領(lǐng)域的模型應(yīng)用，在這些領(lǐng)域的實際問題中，上述模型能夠在很大程度上解決模型解釋性、人工數(shù)據(jù)生成和零樣本學(xué)習(xí)問題。因此在下面的實驗中，我使用 beta-VAEs 模型對心電圖（ETC）數(shù)據(jù)和和比特幣（BTC）的價格數(shù)據(jù)進行了分析。該實驗的代碼在 Github上可以找到。

首先，我使用veta-VAE（一個非常簡單的多層神經(jīng)網(wǎng)絡(luò)）對PTB診斷數(shù)據(jù)中的心電圖數(shù)據(jù)進行了建模，該數(shù)據(jù)包含三類變量：心電圖圖表，每個人隨著時間變化的脈搏數(shù)據(jù)，以及診斷結(jié)果（即是否存在梗塞）。在 VAE 訓(xùn)練過程中，epoch 大小設(shè)置為 50，bottleneck size 設(shè)置為 10，學(xué)習(xí)率為 0.0005，capacity 參數(shù)設(shè)置為 25（參數(shù)設(shè)置參考了這個GitHub項目）。模型的輸入是心跳。經(jīng)過訓(xùn)練，該模型學(xué)習(xí)到了數(shù)據(jù)集中影響變量的實際因素。

下圖展示了我使用其中一個單一特征對心跳數(shù)據(jù)進行操作的過程，其中黑線代表心跳，使用的特征數(shù)據(jù)值從 -3 逐漸增大至 3。在這一過程中，其他特征始終保持不變。不難發(fā)現(xiàn)，第 5 個特征對心跳形式的影響很大，第 8 個代表了心臟病的情況（藍色心電圖代表有梗塞癥狀，而紅色則相反），第 10 個特征可以輕微地影響脈博。

圖：對心電圖的心跳進行解耦

正如預(yù)期的一樣，金融數(shù)據(jù)的實驗效果沒有這么明顯。模型的訓(xùn)練參數(shù)設(shè)置與上一實驗相似。使用的數(shù)據(jù)為 2017 年收集的比特幣價格數(shù)據(jù)集，該數(shù)據(jù)集包含一個時間長度為 180 分鐘的比特幣價格變化數(shù)據(jù)。預(yù)期的實驗效果為使用 beta-VAE 學(xué)習(xí)一些標(biāo)準(zhǔn)的金融時間序列模型，如均值回歸的時間序列模型，但實際很難對所獲得的表示進行解釋。在實驗結(jié)果中可以發(fā)現(xiàn)，第 5 個特征改變了輸入的時間序列的趨勢，第 2、4、6 個特征增加/減少了時間序列上不同階段的波動，或者說使其更加趨于穩(wěn)定或動蕩。

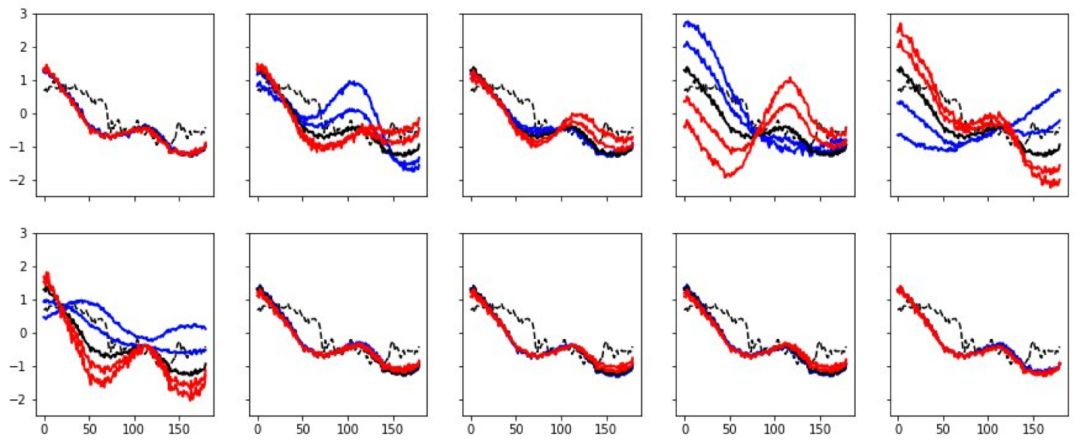
圖：對比特幣的收盤價格進行解耦

多個對象的解耦

假設(shè)在圖像中包含多個對象，我們想要找出每一個對象的影響因素。下面的動圖展示了模型的效果。

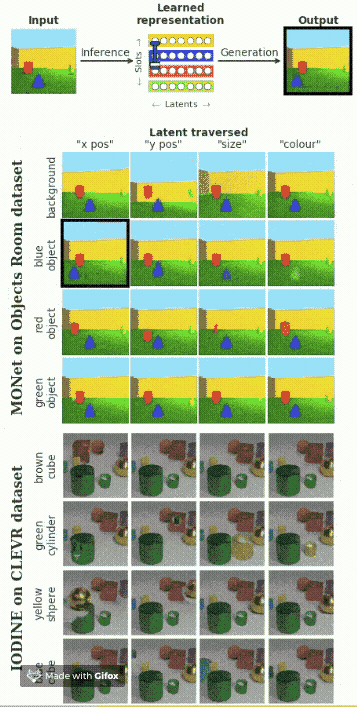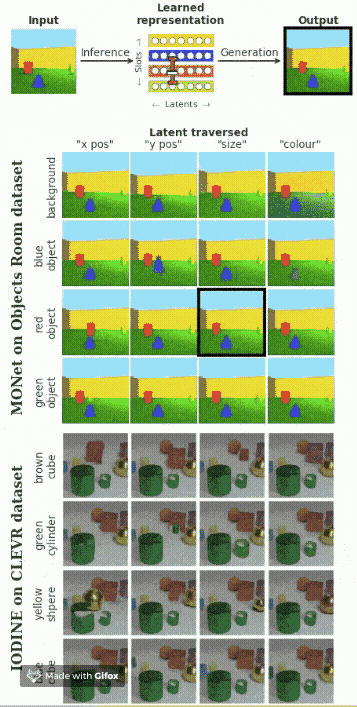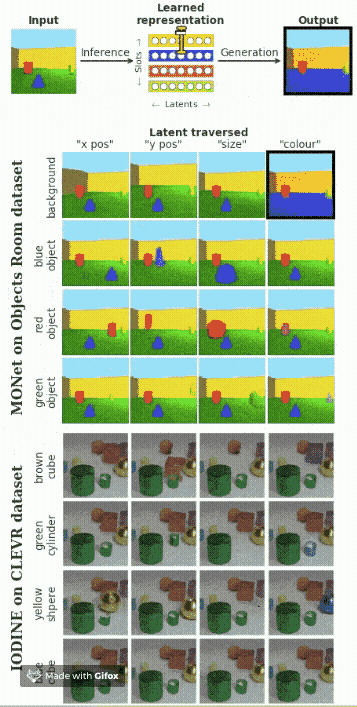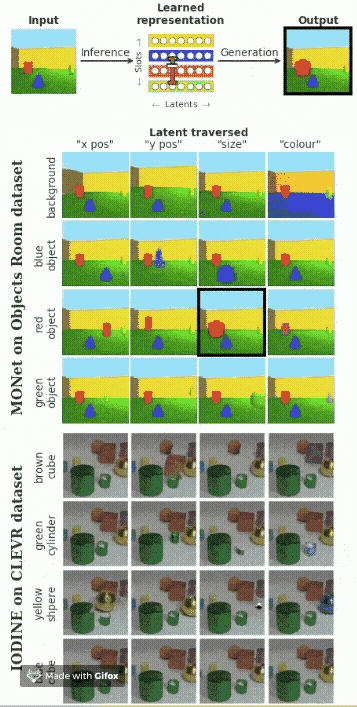
總結(jié)

下面針對于機器學(xué)習(xí)存在的問題列表對 beta-VAE 模型進行總結(jié)：

可解釋性：特征完全可解釋，我們只需要對每個具體嵌入的元素進行驗證。

數(shù)據(jù)需求量大：由于該模型屬于深度學(xué)習(xí)框架，數(shù)據(jù)需求量依然較大。

無監(jiān)督學(xué)習(xí)：可以實現(xiàn)完全的無監(jiān)督學(xué)習(xí)。

零樣本學(xué)習(xí)：可以進行，在文中展示的強化學(xué)習(xí)應(yīng)用就屬于這一類。

對象生成：和普通的 VAE 一樣易于對參數(shù)進行采樣。

對象操作：可以輕松操作任何感興趣的變量。

理論基礎(chǔ)：有待研究。

上文的模型幾乎具備了數(shù)學(xué)建模的全部優(yōu)質(zhì)特性，也具有深度學(xué)習(xí)在分析復(fù)雜數(shù)據(jù)時的高準(zhǔn)確度。那么，如果能使用完全無監(jiān)督的方式，從復(fù)雜數(shù)據(jù)中學(xué)習(xí)到如此好的表示結(jié)果，是不是意味著傳統(tǒng)數(shù)學(xué)建模的終結(jié)？如果一個機器學(xué)習(xí)模型就可以對復(fù)雜模型進行構(gòu)建，而我們只需要進行特征分析，那還需要基于人工的建模嗎？這個問題還有待討論。