摘要晶體中原子的排列具有平移對稱性，平移對稱性限制了晶體只有n=1，2，3，4，6次轉動對稱。發現有8-次，10-次，12-次轉動對稱的準晶。準晶結構是高維晶體結構的投影。晶體和準晶的定義統一于點狀衍射花樣。

1 晶體沒有五次旋轉軸

大自然為我們呈現了一種絕美的物質結構——晶體，金剛石、水晶、硫磺等等都是天然晶體。晶體有非常規則、對稱的外觀。就是從晶體小面(facet)的夾角為某些固定值的觀察事實，人們意識到晶體是由具有固定幾何形狀的單胞(unitcell)在空間中堆垛而來的——晶體學首先是幾何學。用數學的語言來描述，晶體具有這樣的性質：若在空間某個點 r(x，y，z) 上有原子，存在三個線性不相關的基矢量a1，a2， a3， 在R = n1a1 + n2a2 + n3a3 + r處(n1， n2， n3 是任意整數) 必有原子。晶體的這個性質，被表述為晶體中原子的排列具有平移對稱性，即晶體中任意由矢量n1a1 + n2a2 + n3a3聯系的兩點，是等價的。晶體具有平移對稱性帶來的一個重要限制是，晶體中只存在n=1，2，3，4，6 次轉動對稱性，即晶體中存在某些方向，以這些方向為軸轉動某個角度后，晶體中的局域原子環境不變(對于完美的晶體，從外觀上也能看出這一點)，這些角度可表示為θ = 2π/n ，n=1，2，3，4，6。考察一個正方體(圖1)，容易看到穿過對邊中心的軸，是2 次轉動軸(C2)，轉過θ = π 角后，注意不到正方體被轉動了；穿過對面中心的軸，是4 次轉動軸(C4)，轉過θ = π/2 角后，注意不到正方體被轉動；穿過對頂角的軸， 是3 次轉動軸(C3)， 轉過θ = 2π/3 角后，注意不到正方體被轉動。在蜂窩那樣的晶體結構中，穿過每個六角形單元中心的軸是6 次轉動軸。那么，怎么證明晶體的轉動軸只允許n=1，2，3，4，6 這幾種情形呢？

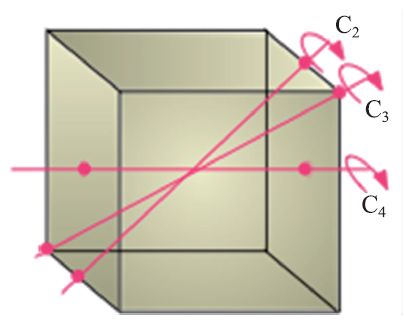
圖1 正方體的2-次、3-次和4-次轉動軸

證明如下，見圖2。若晶體允許n 次轉軸，考察某個方向上相鄰的三個原子。繞過原子O 的n 次軸將聯系OA 的線段順時針轉過θ = 2π/n 角，原子A落在點A'上；繞過原子O 的n 次軸將聯系OB 的線段逆時針轉過θ = 2π/n 角，原子B落在點B'上。按照平移對稱性和轉動對稱性的定義，點A' 和點B'也都是等價的原子占位，線段A' B'與AB平行，其長度必是OA長度的整數倍，即2cos(2π/n) 必須是個整數，解為n=1，2，3，4，6。其中，n=1是平凡的，可以忽略。關于這個問題的證明，是固體物理的常識。

圖2 平移對稱與轉動對稱性的關聯

2 準晶

細心的讀者可能已經注意到了，晶體中沒有5 次轉軸，n=5 被跳過了。跳過就跳過了，沒啥遺憾的，大自然的奧妙自有其合理處。但也有人把找到5 次對稱的鋪排方式(Tessellation. 晶體可以理解為用同一種磚塊鋪滿整個空間的結果)當成挑戰。作為數學游戲，彭羅斯(Roger Penrose，1931— )于1974 年給出由兩種結構單元組成的彭羅斯鋪排圖案，該二維圖案整體上具有5 次轉動對稱性(圖3)。彭羅斯的鋪排方案，用了兩種磚塊且沒有平移對稱性，不算晶體結構。

圖3 一種彭羅斯鋪排

沒有平移對稱性，對于固體物理學家來說麻煩很大的。若一塊固體是晶體，其中原子的位置是有規則的，能用一個簡單的數學表達式寫下來，那關于晶體的定態薛定諤方程（-?2/2m ?2 + V (r))ψ = Eψ 中的勢能V (r)就是可以簡單表達的，晶體中電子的色散關系E = E(k) 就是可解的。解得靠譜不靠譜再說，反正這個過程讓物理學家理解了什么是導體，什么是絕緣體，由此提出了半導體的概念，從而徹底地改變了我們的世界。如果遇到了外觀和內部原子排列看似都很規則的固體，竟然沒有平移對稱性，那固體物理學該如何處理？

有這樣的固體嗎？如果沒有這樣的固體，為什么要杞人憂天呢？

1984 年，人們在Al-Mn 合金的透射電鏡衍射圖像中看到了10 次對稱圖案，這是完美晶體中不會出現的。緊接著在很多樣品中觀察到了10 次對稱衍射花樣(圖4)，由此人們注意到了準晶存在1)。準晶中原子排列是有序的，但沒有平移對稱性，所以被稱為準晶(quasicrystal)。目前確認存在具有8-次，10-次和12-次轉動對稱性的三維準晶。

圖4 AlNiCo合金的電子衍射花樣

準晶的發現，讓許多學科的研究者都很興奮了一陣子，對準晶的研究從數學到文化，從物理到材料，可算是全方位展開。這其中，關于準晶的數學研究，多有出人意料的成果。此前的彭羅斯鋪排圖案，就算是準晶研究的先驅了。5-次轉軸和2π/5 轉角、黃金分割數φ = (√5 + 1)/2 有關。注意，黃金分割數還可以寫成φ = 0.5 × 50.5 + 0.5 ，它和斐波那契數列1， 1， 2， 3，5，8，13，21，34，55，89……有關，是斐波那契數列相鄰兩項之商的極限。斐波那契數列的核心性質是Fn + Fn+1 = Fn+2 ，即每一項的值是前兩項的值之和。按照斐波那契數列方式排列的結構，就和黃金分割數有關系，就和5 次轉動有關。比如，假如有一大一小兩個結構單元，按照小大，小大大，小大大小大…… 方式排列， 這個排列很有序，其每一處的結構模塊由前面兩個結構模塊按照先來后到的方式拼接而成(這就是斐波那契數列的定義)，但是沒有平移對稱性。如圖5中沿著紅線自左下向右上，紅線被黑色方塊切成的線段的排列就是短長，短長長，短長長短長……的方式，這是一維準晶。但是，注意黑方塊組成的二維圖案，將一小一大兩個方塊當成一個結構單元，這是一個簡單方格子(square lattice) 結構，它是二維的晶體。二維晶體在某個方向上的投影，如圖5中方格子在紅線上的投影，竟然是一維準晶！

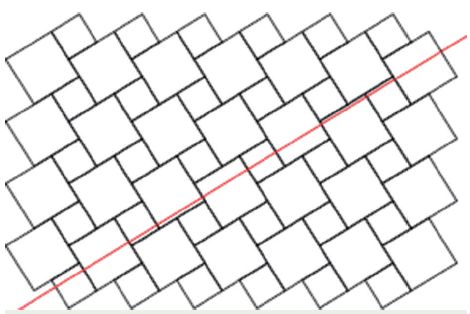
圖5 由一大一小兩個方塊拼在一起作為單元的方格子，其在紅線上的投影是斐波那契數列表征的一維準晶結構

這個關于二維晶體在某個方向上的投影竟然是一維準晶的描述，不是很令人信服。請允許我給個稍微數學嚴謹點的表述。考察二維格子(Z2)，即每個格點的坐標是一對整數(m，n)的方格子2)(圖6)。作直線 y = (φ - 1) ? x 用來投影，過點(0，1)和(1，0)的作線 y = (φ - 1) ? x的平行線(圖6 中的兩條虛線)。考察這兩條平行線所形成的帶狀區域(晶格的一部分)中的格點，將每個格點投影到 y = (φ - 1) ? x 直線上。你會發現，這格點的投影，相互之間只有一大一小兩種間距。從這個意義上說，這些分布是有序的，但是卻沒有平移對稱性。如果你取一部分出來觀察，會發現斐波那契數列描述的分布，那些投影點形成了一維準晶。

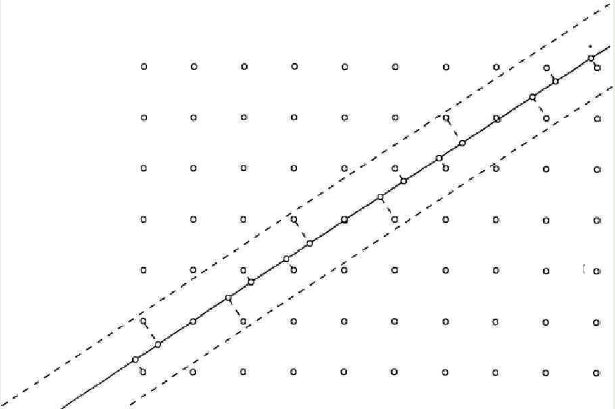
圖6 方格子Z2以及用來投影的直線

這太有趣啦。有序的準晶結構，沒有平移對稱性，但竟然是某個高維晶格的恰當投影(投到恰當選擇的低維對象上)。到高維空間讓我們能夠理解準晶隱蔽的結構。那么，準晶，都是更高維空間中某個晶體結構的投影嗎？是嗎，不是嗎？怎么證明？

要證明準晶是高維晶體的合適的投影，一種是數學意義上的嚴格證明，從某些靠得住的公理、定理出發，邏輯地一步一步導出所有的準晶結構。一種是有點物理味道的證明，如果能找到合適的方法，能構造出準晶作為其投影的高維晶體結構， 擺在那兒， 那也是一種證明！

一旦明確了尋找投影為準晶結構的高維晶體這樣的研究方向，對于熟悉自19 世紀就發展了的高維幾何的數學家來說，這還真不是難事。舉一例來說明一個準備性工作，五種柏拉圖固體中的正十二面體和正二十面體是具有五次轉動軸的，而已發現的晶體中就有十次和十二次準晶，正十二面體就不可避免地成了關注的對象。數學家小試牛刀，發現連接著自中心到正十二面體頂點的12 個矢量是六維歐幾里得空間E6 中6 維正方形對角線組成的交叉到3 維歐幾里得空間E3空間上的投影。1995 年前后，塞內夏爾(M. Senechal)給出了能得到準晶點集的正則投影法和多格網法，非常有效地用于構造投影具有非晶體轉動對稱性的點集的高維晶格。比如，Z5 空間中的5 維立方格子投影到一個面上，可以得到的點集可看作2 維準晶(圖7)。高維空間當然容納更多的結構，不只是準晶結構，其它轉動對稱性的結構也容易找到相應的高維晶格。5-次，10-次，8-次和12-次轉動對稱的平面結構都可以從4維晶格得到。

圖7 5維立方格子投影到一個面上可得到2維準晶(局部)

3 維度啊維度

《三體》中有一個梗，說三體人對咱們地球人的攻擊是“降維攻擊”。這人與人之間的差別不在廣度(extension)，擁有相同維度(dimension)的不同空間能差到哪兒去？怕就怕差在維度上。平面上有一條線，隨機在平面上畫點，點落到線上的概率為零。點當然可以落到那條線上，還可以有無窮多個點落到那條線上，但點落到那條線上的概率依-然-為-零！可憐的1 維的線，面對2 維的面，它都不知道自己的無窮大都是0。

從更高維度看三維真實空間里的物理問題，能看透更多本質性的東西。養成到更多維度的空間中看問題的習慣，物理學家要多向數學家學習。三維(二維)晶體只有n=1，2，3，4，6 次轉動軸的事實，引出了晶體限制定理(crystallographic restriction theorem)。如果我們跳到更多維度的空間里去看這個問題，就要轉換思路。高維空間里的轉動，不再是平面型的(planar)，應使用N×N轉動矩陣討論為宜，關切的是整數矩陣(integer matrix)話題。函數OrdN是N×N轉動矩陣A 允許的階數k，即使得Ak = 1 的k 的取值。對于真實晶體涉及的晶體限制定理，它敘述的事實是Ord2=(1， 2， 3，4， 6)。欲實現8- 次， 10-(5-) 次，12-次轉動，要求轉動矩陣至少是4 × 4。注意Ord4=(5， 8， 10， 12)，準晶恰好是有8-，10-(5-)次，12-次轉動軸，或許這說明準晶與4維空間有緣，它應該就是4 維空間里的晶體。Ord6=(7，9，14，15，18，24)，也許6 維空間離咱們太遠，所以觀察不到7- 次， 9- 次對稱的物質結構。說不定哪天會遇到呢，天知道。

4 后來的事

晶體中的原子具有平移對稱性，準晶中原子排列是有序的，但不具有平移對稱性。準晶與晶體有明顯的可區別的特征。但是，當我們認識到準晶結構必定是高維晶體的投影，此一發現又表明晶體和準晶之間似乎沒有必然的界限。堅持分別晶體和準晶涉嫌犯了執念。這事兒最終的解決方案有點兒出乎意料，原來的晶體和準晶都統一為晶體了，但是晶體的定義改變了。晶體的定義特征不再是原子排列具有平移對稱性，而是說衍射圖案(原子排列的傅里葉變換)由明銳的點組成的結構是晶體。

我們的世界是三維的，人類生活在二維的地表上。早在古希臘時期，關于二維、平直空間的平面幾何就已經成了系統化的知識了，關于三維空間的立體幾何也多有談論，但是高維幾何概念的發展要到19 世紀才由哈密頓(Sir William Rowan Hamilton，1805—1865)、凱雷(Arthur Cayley，1821—1895)，施萊夫利(Ludwig Schl?fli，1814—1895)和黎曼(Bernhard Riemann，1826—1866)等人來開拓。把我們的幾何觀念從習慣的、可經驗的三維世界拓展到四維以上的世界要延宕到19 世紀，原因除了思維慣性以外，很多人頭腦中不能構建高維圖形也是一個重要原因。直觀不行，那就要借助數學的手段，mathematics makes the invisible visible，信矣哉！

順便說一句，由高維晶體投影并不是得到準晶結構的唯一途徑。筆者的學生廖龍光博士就用函數y = arcsin(sin(2πμn))，其中變量n取整數， μ =√2 - 1 和μ =2 -√3 ，分別得到了8-次和12-次準晶結構。這里的奧秘是，熟悉相關的數學并且不辭辛苦地嘗試。旁人能看到的是研究者的靈感，但靈感來自實踐。

1) 準晶雖然是在人工樣品中先發現的，但大自然中存在準晶結構的礦物，準晶原子結構花樣此前也早被人類作為純粹的裝飾圖案構思出來了。

2)也可以把坐標(m，n)表示成m+i·n。這樣的復數稱為高斯整數，筆者就是利用高斯整數證明了方格子在無窮多個方向上具有縮放對稱性，參見筆者著《一念非凡》。