最近在某網站上看到一個視頻,是關于排序算法的可視化的,看著挺有意思的,也特別喜感。
不知道作者是怎么做的,但是突然很想自己實現一遍,而且用python實現特別快,花了一天的時間,完成了這個項目。主要包括希爾排序(Shell Sort)、選擇排序(Selection Sort)、快速排序(Quick Sort)、歸并排序(Merge Sort)等九種排序。
附上源碼鏈接:
https://github.com/ZQPei/Sorting_Visualization
(覺得不錯,記得幫忙點個star哦)
下面具體講解以下實現的思路,大概需要解決的問題如下:
如何表示數組
如何得到隨機采樣數組,數組有無重復數據
如何實現排序算法
如何把數組可視化出來
一、如何表示數組
Python提供了list類型,很方便可以表示C++中的數組。標準安裝的Python中用列表(list)保存一組值,可以用來當作數組使用,不過由于列表的元素可以是任何對象,因此列表中所保存的是對象的指針。這樣為了保存一個簡單的[1,2,3],需要有3個指針和三個整數對象。對于數值運算來說這種結構顯然比較浪費內存和CPU計算時間,再次就不詳細論述。
二、如何得到隨機采樣數組,數組有無重復數據
假設我希望數組長度是100,而且我希望數組的大小也是在[0,100)內,那么如何得到100個隨機的整數呢?可以用random庫。
示例代碼:
import randomdata = list(range(100))data = random.choices(data, k=100)print(data)[52, 33, 45, 33, 48, 25, 68, 28, 78, 23, 78, 35, 24, 44, 69, 88, 66, 29, 82, 77, 84, 12, 19, 10, 27, 24, 57, 42, 71, 75, 25, 1, 77, 94, 44, 81, 86, 62, 25, 69, 97, 86, 56, 47, 31, 51, 40, 21, 41, 21, 17, 56, 88, 41, 92, 46, 56, 80, 23, 70, 49, 96, 83, 54, 16, 36, 82, 24, 68, 60, 16, 98, 16, 81, 10, 13, 11, 24, 68, 35, 56, 39, 23, 44, 6, 30, 3, 60, 56, 66, 38, 28, 47, 47, 25, 90, 89, 38, 68, 21]
但是以上代碼有個問題,random.choices是對一個序列進行重復采樣,得到的數組存在重復數據,那如果不希望存在重復數據,而是希望進行無重復采樣,怎么辦?
可以用random.sample函數,示例代碼:
data = random.sample(data, k=100)print(data)[49, 28, 56, 28, 44, 62, 81, 25, 48, 33, 54, 38, 30, 16, 13, 19, 23, 56, 60, 66, 41, 24, 68, 68, 77, 92, 78, 24, 66, 3, 80, 94, 78, 41, 84, 88, 21, 56, 25, 25, 75, 24, 38, 82, 31, 52, 23, 10, 71, 40, 27, 46, 33, 35, 56, 51, 1, 23, 12, 25, 89, 16, 21, 21, 11, 42, 47, 44, 81, 35, 86, 88, 29, 36, 77, 16, 39, 6, 57, 69, 96, 68, 24, 86, 97, 90, 69, 10, 68, 98, 56, 44, 83, 47, 70, 17, 47, 82, 60, 45]
這樣就可以得到無重復采樣數據了。
三、如何實現排序算法
算法種類較多,就不一一舉例;再次就以希爾排序(Shell Sort)為例講講:
爾排序的原理:希爾排序(Shell Sort)是插入排序的一種。也稱縮小增量排序,是直接插入排序算法的一種更高效的改進版本。
希爾排序是把記錄按下標的一定增量分組,對每組使用直接插入排序算法排序;隨著增量逐漸減少,每組包含的關鍵詞越來越多,當增量減至1時,整個文件恰被分成一組,算法便終止。
基礎的插入法排序是兩重循環,希爾排序是三重循環,最外面一重循環,控制增量gap,并逐步減少gap的值。二重循環從下標為gap的元素開始比較,依次逐個跨組處理。最后一重循環是對組內的元素進行插入法排序。這樣進行排序的優點在于每次循環,整個序列的元素都將小元素的值逐步向前移動,數值比較大的值向后移動。
示例代碼:
from data import DataSeqdef ShellSort(ds): assert isinstance(ds, DataSeq), "Type Error" Length = ds.length D = Length//2 while D>0: i=0 while i
四、如何把數組可視化出來
有了隨機數組初始化方法,再實現好排序函數,我們還差一步,就是把排序函數中每次移動數組后將數組可視化并輸出。
對數組進行可視化,很容易想到Python的可視化工具matplotlib!但是在項目中我并沒有用matplotlib,而是用了numpy+opencv。
為什么不用matplotlib?
因為在排序過程中,每次修改數組,都希望能夠實時修改圖片并輸出,matplotlib確實很方便,但是matplotlib的效率實在是不高,而且每次修改數組前后的兩幅圖片其實是差不多的。如果用matplotlib,每次都是要重新繪制圖片,非常耗時!!!
所以考慮自己生成圖片,在每次修改數組后,只將圖片中改動的那兩列進行修改即可!這樣就比用matplotlib每次重新繪制圖片效率高得多!
數組中主要有兩種操作,一種是對某個idx賦值,一種是交換某兩個idx的值。
示例代碼:
class DataSeq: WHITE = (255,255,255) RED = (0,0,255) BLACK = (0,0,0) YELLOW = (0,127,255) def __init__(self, Length, time_interval=1, sort_title="Figure", repeatition=False): pass def Getfigure(self): _bar_width = 5 figure = np.full((self.length*_bar_width,self.length*_bar_width,3), 255,dtype=np.uint8) for i in range(self.length): val = self.data[i] figure[-1-val*_bar_width:, i*_bar_width:i*_bar_width+_bar_width] = self.GetColor(val, self.length) self._bar_width = _bar_width self.figure = figure def _set_figure(self, idx, val): min_col = idx*self._bar_width max_col = min_col+self._bar_width min_row = -1-val*self._bar_width self.figure[ : , min_col:max_col] = self.WHITE self.figure[ min_row: , min_col:max_col] = self.GetColor(val, self.length) def SetVal(self, idx, val): self.data[idx] = val self._set_figure(idx, val) self.Visualize((idx,)) def Swap(self, idx1, idx2): self.data[idx1], self.data[idx2] = self.data[idx2], self.data[idx1] self._set_figure(idx1, self.data[idx1]) self._set_figure(idx2, self.data[idx2]) self.Visualize((idx1, idx2))
詳細代碼見github:
https://github.com/ZQPei/Sorting_Visualization
(就等你的小小star)其他的都沒有什么了,有細節的問題可以在我的github下面留言勾搭。
最后附上一張效果圖:
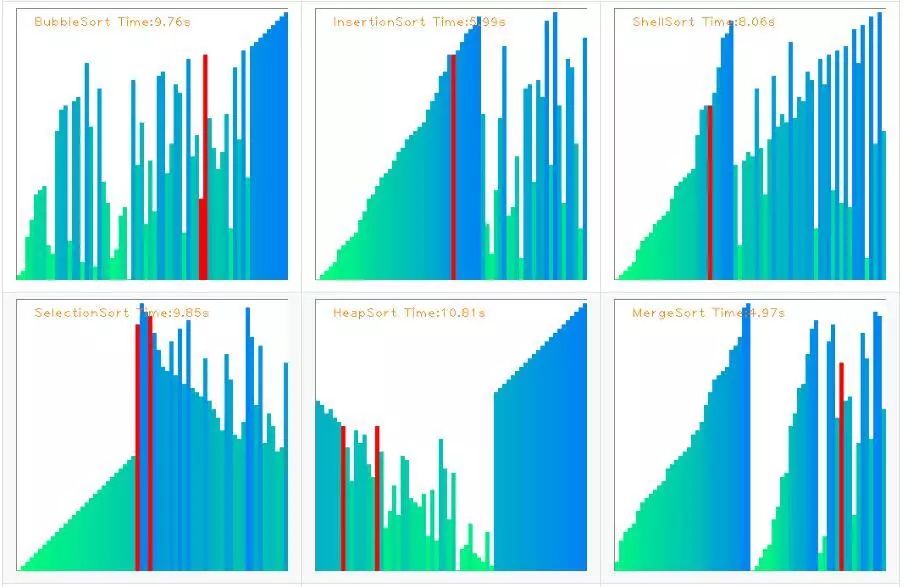
-
C++
+關注
關注
22文章
2112瀏覽量
73717 -
可視化
+關注
關注
1文章
1198瀏覽量
20972 -
python
+關注
關注
56文章
4800瀏覽量
84820
原文標題:3分鐘快速實現:9種經典排序算法的可視化
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 9種經典排序算法的可視化
9種經典排序算法的可視化











評論