最新研究提出，圖神經網絡僅對特征向量進行低通濾波，不具有非線性流形學習特性。論文提出了一種基于圖形信號處理的理論框架，用于分析圖神經網絡。

圖神經網絡已成為解決圖結構數據機器學習問題的最重要技術之一。

最近關于頂點分類(vertex classification)的工作提出了深度和分布式的學習模型，以實現高性能和可擴展性。

但最近，一篇題為“Revisiting Graph Neural Networks: All We Have is Low-Pass Filters”的論文引起關注，文中提出，圖神經網絡僅僅是對特征向量進行低通濾波而已。

來自東京工業大學、RIKEN的兩位研究人員發現，基準數據集的特征向量對于分類任務來說已經能提供很多有用信息，而圖結構僅僅提供了一種對數據進行去燥的方法。

論文提出了一種基于圖形信號處理的理論框架，用于分析圖神經網絡。

作者稱，他們的結果表明，圖神經網絡僅對特征向量進行低通濾波(low-pass filtering)，不具有非線性流形學習特性。論文進一步研究了它們對特征噪聲的適應力，并對基于GCN的圖神經網絡設計提出了一些見解。

什么時候應該使用圖神經網絡？

圖神經網絡(Graph neural networks, GNN)是一類能夠從圖結構數據中學習的神經網絡。近年來，用于頂點分類和圖形同構測試的圖神經網絡在多個基準數據集上取得了良好的效果，并不斷開創新的最先進技術性能。隨著ChebNet和GCN在頂點分類方面獲得成功，許多GNN變體被提出來解決社交網絡、生物學、化學、自然語言處理、計算機視覺和弱監督學習方面的問題。

在半監督頂點分類問題中，我們觀察到，圖卷積層(GCN)的參數只會導致過擬合。類似的觀察在簡單的架構(如SGC)和更復雜的腳骨(如DGI)中都曾被報告。

基于這種現象，Felix Wu等人提出將圖神經網絡簡單地看作是特征傳播(feature propagation)，并提出了一種在許多基準數據集上具有最先進性能的高效模型。Kawamoto等人對圖分區設置下未經訓練的GCN-like GNNs進行了相關理論評述。

從這些先前的研究中，一個很自然的問題出現了：為什么、以及何時圖神經網絡在頂點分類任務中表現很好？

換句話說，是否存在一個頂點特征向量的條件，使得圖神經網絡模型即使沒有經過訓練也能很好地工作？

那么，我們能否找到基準圖神經網絡(如SGC或GCN)失敗的實際反例?

在本研究中，我們從圖信號處理的角度來回答上述問題。在形式上，我們考慮了一個圖的半監督學習問題。

給定一個圖G = (V, E)，每個頂點i∈V都有一個特征x(i)∈x，和標記y(i)∈y，其中x是d維歐氏空間R d, Y = R用于回歸， Y ={1，…， c}用于分類。任務是從特征x(i)中學習預測標簽y(i)的假設。

然后，我們描述了這個問題的圖神經網絡解決方案，并對最常用的基準模型GCN及其簡化的變體SGC的機制提供了見解。

本研究三大貢獻

圖信號處理(Graph signal processing, GSP)將頂點上的數據視為信號，應用信號處理技術來理解信號的特征。通過組合信號(特征向量)和圖結構(鄰接矩陣或鄰接矩陣的變換)，GSP啟發了圖結構數據學習算法的發展。在標準信號處理問題中，通常假設觀測值包含一些噪聲，并且底層的“真實信號”具有低頻。這里，我們對我們的問題提出了類似的假設。

假設1：輸入特征包括低頻真實特征和噪聲。真實特征為機器學習任務提供了足夠的信息。

本研究的第一個貢獻是驗證了常用數據集的假設1(第3節)。圖1顯示了針對不同頻率成分(frequency components)的特征訓練的2層感知器(MLPs)的性能。在所有基準數據集中，我們看到只有少數頻率成分有助于學習。在特征向量中加入更多的頻率成分只會導致性能下降。反過來，當我們將高斯噪聲N (0, σ2 ) 添加到特征中時，分類精度變得更糟了。

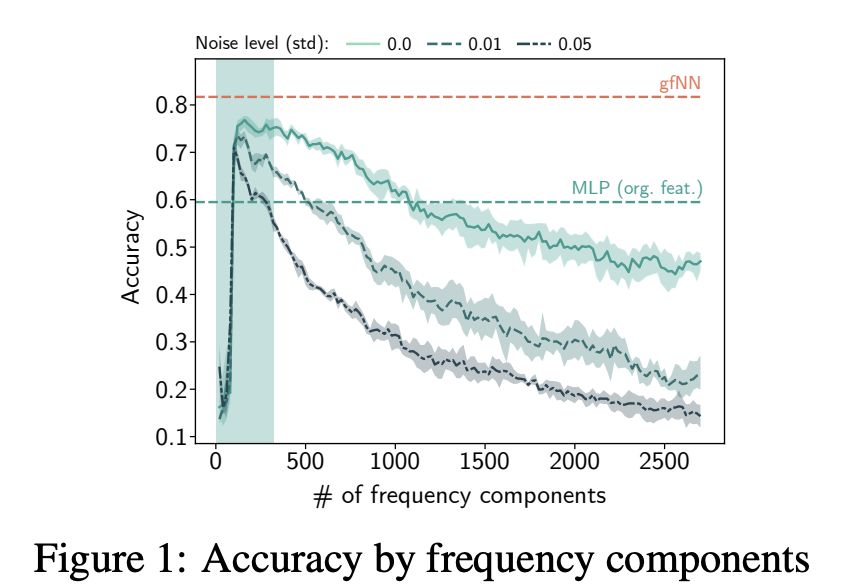
圖1：頻率成分的精度

最近的許多GNN都是建立在圖信號處理的基礎上的。最常見的做法是用(增強)規范化鄰接矩陣I ? L? 和矩陣X的特性。在圖信號處理的文獻中，這種操作在圖上過濾信號(filters signals)，而不顯式地對標準化拉普拉斯矩陣進行特征分解。在這里，我們將這個增強的標準化鄰接矩陣及其變體稱為可互換的圖濾波器(graph filters)和傳播矩陣(propagation matrices)。

本研究的第二個貢獻表明，將圖信號與傳播矩陣相乘對應于低通濾波(第4節，尤其是定理3)，此外，我們還證明了觀測信號與低通濾波器之間的矩陣乘積是真實信號優化問題的解析解。與最近的圖神經網絡設計原理相比，我們的結果表明圖卷積層只是低通濾波(low-pass filtering)。因此，不需要學習圖卷積層的參數。

在理論理解的基礎上，我們提出了一種新的基準框架，稱為gfNN((graph filter neural network, 圖濾波神經網絡)，對頂點分類問題進行了實證分析。

gfNN由兩個步驟組成：

通過與圖濾波矩陣的乘法實現濾波特性;

通過機器學習模型學習頂點標簽。

我們使用圖2中的一個簡單實現模型演示了框架的有效性。

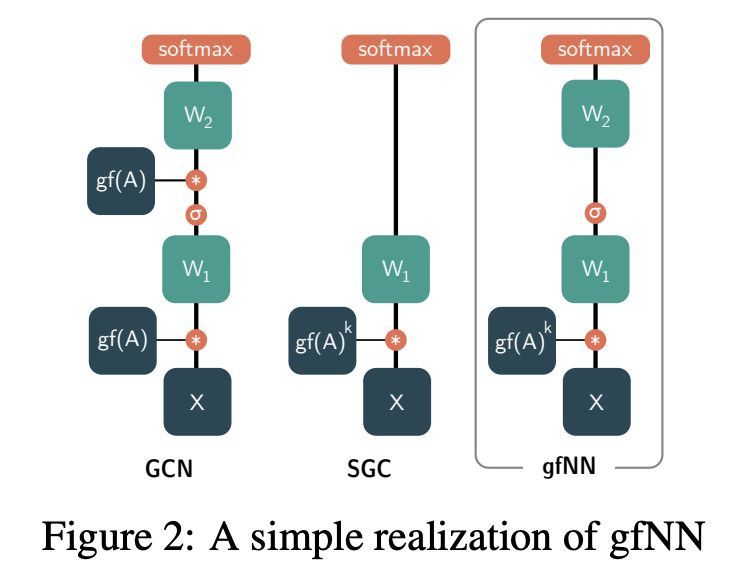
圖2：gfNN的一個簡單實現

本研究的第三個貢獻是以下定理：

定理2：在假設1下，SGC、GCN和gfNN的結果與使用真實特征的相應神經網絡的結果相似。

定理7表明，在假設1下，gfNN和GCN具有相似的高性能。由于gfNN在學習階段不需要鄰接矩陣的乘法，因此它比GCN要快得多。此外，gfNN對噪聲的容忍度也更高。

最后，我們將gfNN與SGC模型進行了比較。雖然SGC在基準數據集上計算速度快、精度高，但我們的分析表明，當特征輸入是非線性可分的時，SGC會失敗，因為圖卷積部分對非線性流形學習沒有貢獻。為了實證證明這個觀點，我們創建了一個人工數據集。

實驗和結果

為了驗證前面提出的觀點，我們設計了兩個實驗。在實驗E1中，我們將不同水平的白噪聲加入到真實數據集的特征向量中，并比較不同基線模型的分類精度。

在實驗E2中，我們研究了一個具有復雜的特征空間的人工數據集，以證明SGC等簡單模型在分類時會失敗。

表1給出了每個數據集的概述。

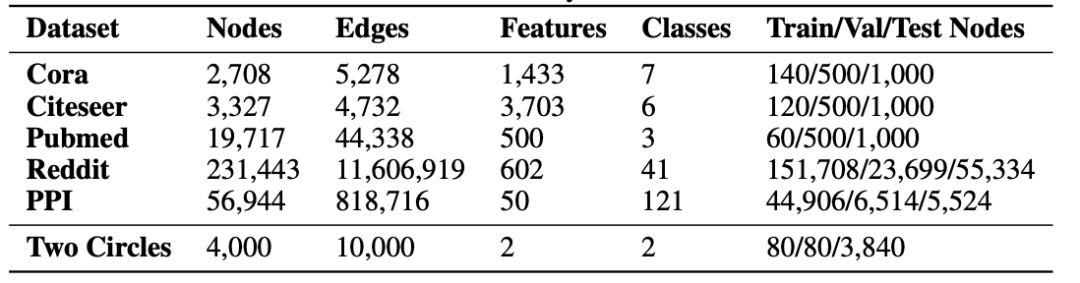
表1：用于頂點分類的實際基準數據集和合成數據集

神經網絡

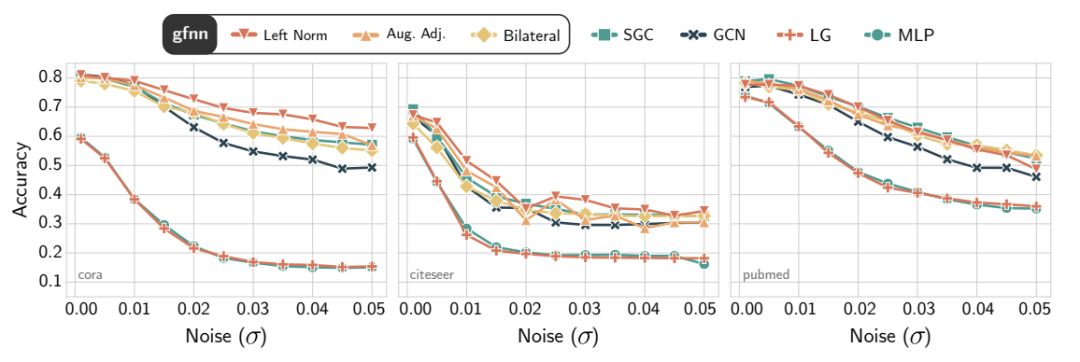
圖4:Cora(左)、Citeseer(中)和Pubmed(右)數據集上的基準測試精度。噪聲水平通過在特征值上增加白噪聲的標準差來測量。

圖像濾波器的去噪效果

對于每個數據集表1中,我們介紹一個白噪聲N(0, 2)為特征向量?范圍內(0.01,0.05)。根據定理8和定理7的含義，由于GCN的一階去噪特性，它對特征噪聲的容忍度較低。

隨著噪聲水平的增加，我們在圖4中可以看到，GCN、Logistic回歸(LR)和MLP更容易對噪聲進行過擬合。另一方面，gfNN和SGC對噪聲的容忍度差不多。

圖過濾器的表現力

圖5：基于兩個圓形圖案生成的500個數據樣本的決策邊界

表2：隨機train/val/test分段的平均測試精度(5次)

總結

很少有工作涉及GCN架構的限制。Kawamoto等人采用平均場方法對一個簡單的GCN模型進行了統計物理分析。他們的結論是，反向傳播既不能提高基于GCN的GNN模型的準確性，也不能提高其可檢測性。Li et al.在有限的標簽數據設置下對多層的GCN模型進行了實證分析，指出如果標簽數據太少或者疊加層太多，GCN的性能就會下降。雖然這些結果為GCN提供了很有洞察力的觀點，但是它們并沒有充分地回答這個問題：我們什么時候應該使用GNN?

我們的結果表明，如果假設1成立，我們應該使用GNN方法來解決給定的問題。從我們的角度來看，從GCN派生出來的GNNs只是簡單地執行噪聲濾波，并從去噪數據中學習。

基于我們的分析，我們提出了GCN和SGC可能無法執行的兩種情況：噪聲特征和非線性特征空間。然后，我們提出一個在這兩種情況下都能很好地工作的簡單方法。

近年來，基于GCN的神經網絡在點云分析、弱監督學習等領域得到了廣泛的應用。隨著輸入特征空間的復雜化，我們提議重新審視當前基于GCN的GNNs設計。在計算機視覺中，GCN層并不是卷積層，我們需要把它看作一種去噪機制。因此，簡單地疊加GCN層只會給神經網絡設計帶來過擬合和復雜性。