對于那些擅長于用微分方程、概率論解決問題的數(shù)學(xué)家們來說，素有“黑盒子”之稱機(jī)器學(xué)習(xí)往往是要被踢到鄙視鏈底端的。

但是，在與各行各業(yè)中，絕大多數(shù)公司（小到初創(chuàng)公司，大到國際巨鱷）都在尋求運(yùn)用機(jī)器學(xué)習(xí)的方法。隨著企業(yè)不斷地將機(jī)器學(xué)習(xí)融入其文化與組織中，這事也變得越來越普遍。

有意思的是，在本科和碩士教育中，數(shù)學(xué)專業(yè)內(nèi)部居然也都彌漫起了機(jī)器學(xué)習(xí)的熱潮。舉例說，牛津大學(xué)的“深度學(xué)習(xí)理論”碩士課程在其設(shè)立的第一年就被超額報名。

更驚人的是，很多數(shù)學(xué)博士生打算將機(jī)器學(xué)習(xí)嵌入到它們的研究課題中，從而形成將“傳統(tǒng)”（ODE和PDE）和“現(xiàn)代”（深度學(xué)習(xí)）相結(jié)合和新型混合模型。

所以，機(jī)器學(xué)習(xí)是否會最終取代數(shù)學(xué)建模？

如果數(shù)學(xué)模型在科研領(lǐng)域無法突破，我們最終是否會使用機(jī)器學(xué)習(xí)的方法來獲得建模上的進(jìn)展呢？

當(dāng)然不是！我認(rèn)為，機(jī)器學(xué)習(xí)和數(shù)學(xué)模型應(yīng)當(dāng)是互補(bǔ)的關(guān)系——充分結(jié)合二者的力量一定會產(chǎn)生有趣的新模型。

為了說明我的觀點(diǎn)，我構(gòu)想了一個例子，讓我們開啟一趟科技文明之旅！在這個虛構(gòu)的文明中，機(jī)器學(xué)習(xí)相當(dāng)發(fā)達(dá)，然而這個文明的數(shù)學(xué)卻糟糕得很，尤其是還不會微積分。

一個虛構(gòu)的文明

假設(shè)我們正處于一個微積分落后但深度學(xué)習(xí)發(fā)達(dá)的科技文明中。

和大多數(shù)文明一樣，它們都致力于用炮彈攻擊自己的對手。兩位來自同一陣營的科學(xué)家在對他們剛發(fā)行的大炮的攻擊范圍進(jìn)行建模。

科學(xué)家可以控制下列因素：

大炮里裝載的彈藥總量（例如炮彈的發(fā)射速度）

大炮的角度

科學(xué)家可以測量下列內(nèi)容：

彈丸從大炮中射出去的直線距離。

*假設(shè)地面完全水平。

從數(shù)學(xué)的角度上，他們希望找到一個模型/函數(shù)F，這個函數(shù)能基于所有速度v和角度θ進(jìn)行預(yù)測。

s=F(v,θ)

使得這個結(jié)果接近于真實(shí)的行進(jìn)距離。

由于沒有炮彈在空中移動的相關(guān)知識儲備，科學(xué)家們采用了數(shù)據(jù)驅(qū)動的方式。

數(shù)據(jù)采集

科學(xué)家們用一天的時間來以各種火力及角度進(jìn)行大炮射擊。每次他們點(diǎn)火發(fā)射，他們都會測量發(fā)射點(diǎn)和炮彈終點(diǎn)間的距離。但是，他們的測量結(jié)果并不完全精確，每次測量都會引入一些誤差。

在那一天的時間中，他們打算發(fā)射1000次炮彈，產(chǎn)生1000個三元數(shù)組(vi,θi,si)，其中θi是弧度制的。

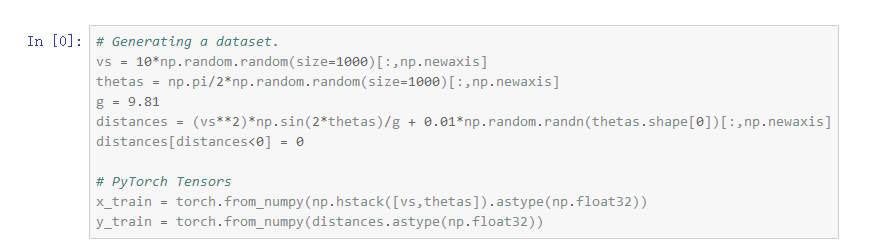
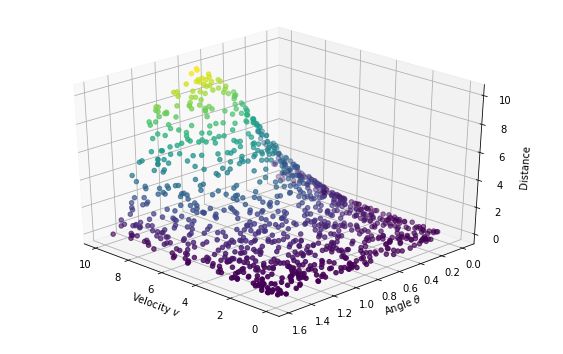
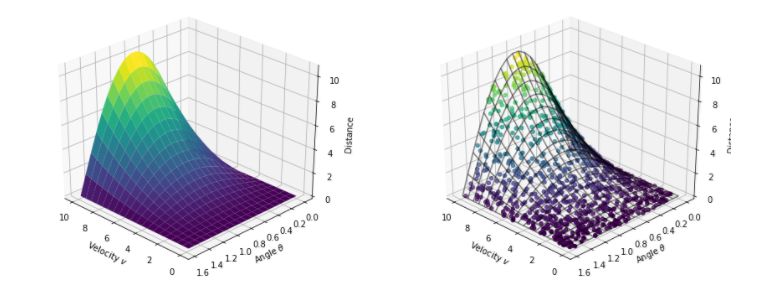
這些數(shù)據(jù)點(diǎn)分布如下圖所示：

不用模型的方法

解決問題的最簡單方法就是不使用模型，因?yàn)閿?shù)據(jù)就能化身為模型！在這種方法中，他們選用那些最接近于他們想預(yù)測的情景的歷史數(shù)據(jù)，使用這些歷史數(shù)據(jù)當(dāng)作預(yù)測模型（即KNN模型）。例如：

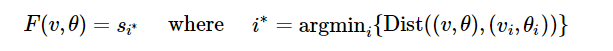
這種純數(shù)據(jù)驅(qū)動的方式有著明顯的缺點(diǎn)。如果他們獲得的數(shù)據(jù)不能覆蓋所有的輸入可能性，或者數(shù)據(jù)過于稀疏，這種方式就會產(chǎn)生問題。在這個例子中，如果要預(yù)測速度大于10的射擊距離，沒有模型的話他們就無法進(jìn)行精準(zhǔn)預(yù)測。

基于線性模型的方法

從數(shù)據(jù)看來，他們期望的函數(shù)是非線性的，而且線性模型不可能將結(jié)果預(yù)測得很準(zhǔn)確。但是，線性模型并非完全沒有價值，在很多應(yīng)用場景下它是一種基礎(chǔ)模型，所以這兩位科學(xué)家決定先用個線性模型試試。

線性模型的數(shù)學(xué)表達(dá)如下：

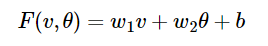
在表達(dá)式中，wi∈R是權(quán)重，b∈R是偏移項(xiàng)，這些值都會被確定下來。我們用PyTorch實(shí)現(xiàn)線性模型，并使用隨機(jī)隨機(jī)梯度下降法（當(dāng)然還有其他更好更簡單的方法）尋找模型參數(shù)。

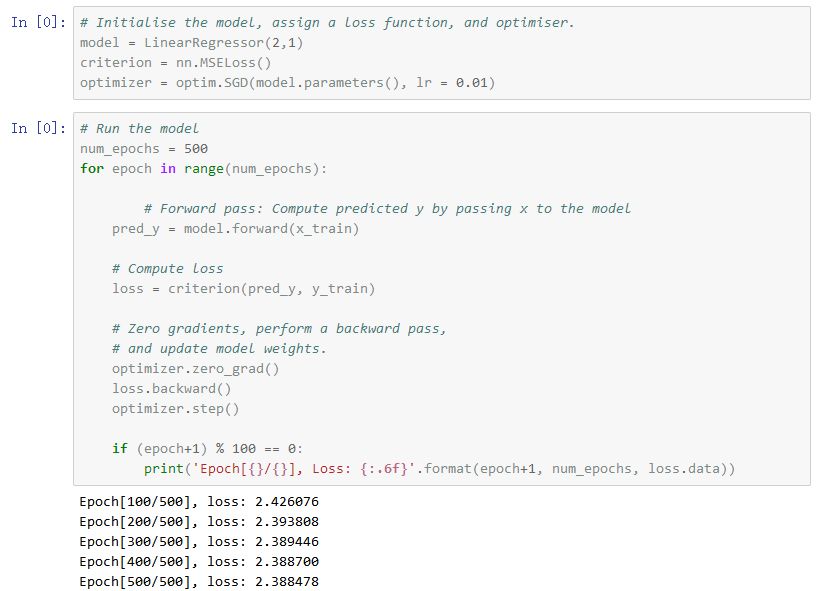
正如預(yù)期的那樣，建模結(jié)果非常糟糕。

“黑盒”登場——深度神經(jīng)網(wǎng)絡(luò)

科學(xué)家們在機(jī)器學(xué)習(xí)研究和計(jì)算框架設(shè)計(jì)方面投入了大量資金，因此他們在面對問題時喜歡以深度神經(jīng)網(wǎng)絡(luò)的方式構(gòu)想解決方案。說白了就是，他們喜歡使用多層感知器系統(tǒng)，它包含有多個線性層，層與層之間靠非線性激活函數(shù)相連。模型可以按如下形式描述：

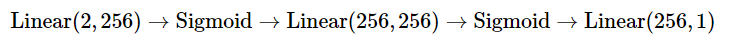
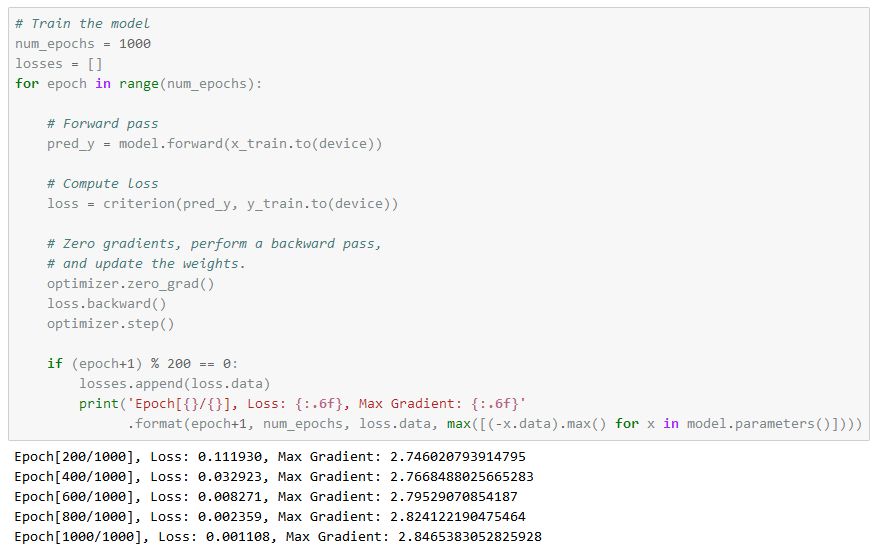
我們用Adam optimizer對模型進(jìn)行訓(xùn)練，結(jié)果如下：

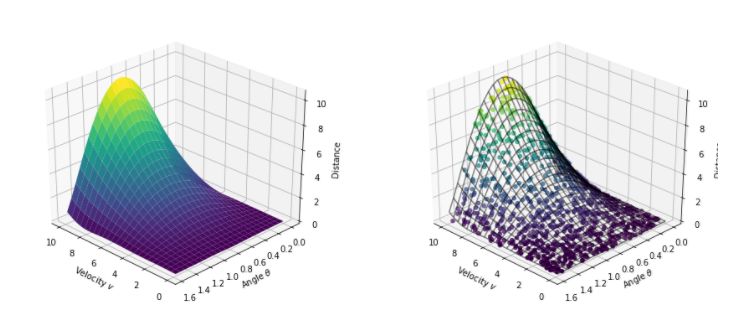
對于在這方面沒有經(jīng)驗(yàn)的人，在看到神經(jīng)網(wǎng)絡(luò)的預(yù)測結(jié)果的時候，基本都會感到驚嘆！至今為止，這也是深度學(xué)習(xí)流傳盛廣的主要原因——它不但有用，且效果顯著。只是我們并不知道為什么。

用數(shù)學(xué)語言刻畫“準(zhǔn)線性方法”

在上述的黑匣子模型中，科學(xué)家們有一個能夠準(zhǔn)確預(yù)測大炮射擊距離的模型，但顧名思義，他們對模型的形式?jīng)]有直觀理解。科學(xué)家們熱衷于在使用機(jī)器學(xué)習(xí)方法的同時恢復(fù)這種直觀理解，并重新使用線性模型。

我們高中的時候都學(xué)過三角函數(shù)，科學(xué)家們認(rèn)為這個問題可能會涉及一些三角函數(shù)與速度的乘積。于是他們把模型寫成非線性基函數(shù)的線性組合：

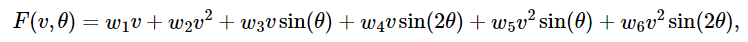
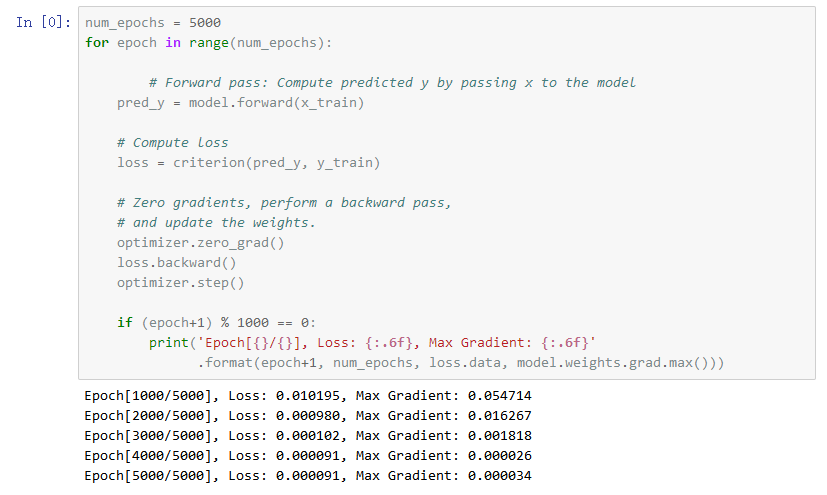
把非線性嵌入到線性模型之后，模型可以像線性模型一樣計(jì)算參數(shù)。優(yōu)化后，模型為：

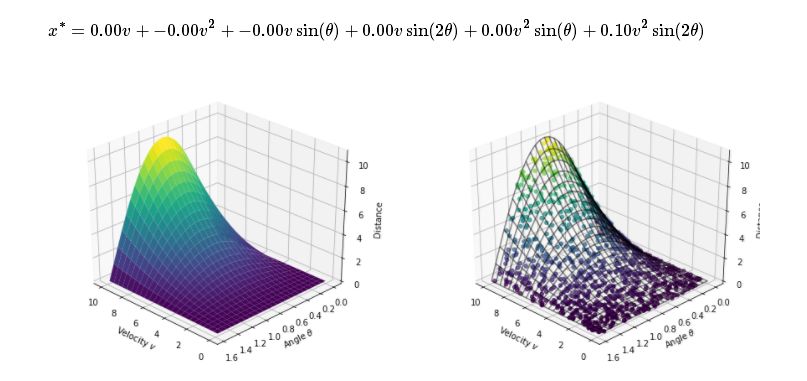
在這種情況下，除了sin(2θ)的參數(shù)，優(yōu)化將其他所有參數(shù)歸零。

將F與數(shù)據(jù)進(jìn)行比較，他們發(fā)現(xiàn)模型非常具有預(yù)測性。不僅如此，模型的公式短小精練！當(dāng)然，他們能選中三角函數(shù)也是非常“幸運(yùn)”了。

數(shù)學(xué)方法——無數(shù)據(jù)模型

很多年后，微積分終于被發(fā)現(xiàn)了！于是，兩位老科學(xué)家開始重新審視這個問題。

1.假設(shè)方程

低速炮彈的物理模型非常簡單。炮彈有垂直向下的重力加速度，恒定為-g。由于在x方向上沒有作用在射彈上的力，它始終保持其初始速度。該模型可以寫成二階微分方程組：

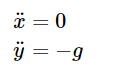
初值條件為：

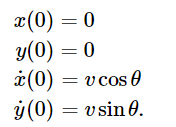
后兩個方程式描述了炮彈最初發(fā)射時的速度的水平和垂直分量。這些方程描述了系統(tǒng)，但如何解決這些問題呢？

2.數(shù)值積分

通常在數(shù)學(xué)中，寫下微分方程是一個簡單的部分，大部分時間都花在試圖解決它們上面！

他們寫出了該問題的一階常微分方程（ODE）：

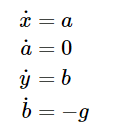
初值條件為：

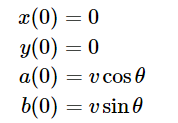
易證這兩個方程相同。

積分在數(shù)學(xué)中無處不在，有多種方法來進(jìn)行數(shù)值積分。最簡單和最直觀的方法是歐拉方程，它從初始點(diǎn)開始，并在該點(diǎn)的梯度方向上走一小步，即：

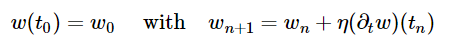
使用數(shù)值積分，可以準(zhǔn)確地預(yù)測炮彈的整個軌跡。

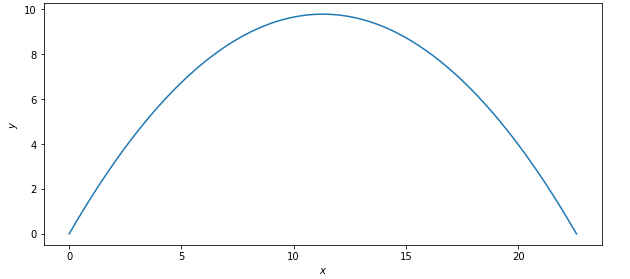
著陸點(diǎn)的位置是x（t*），它們可以從預(yù)測的軌跡中提取。

相比于機(jī)器學(xué)習(xí)模型，這一數(shù)學(xué)模型的一個明顯優(yōu)勢是，我們可以很輕易地解決更復(fù)雜的問題——例如不平坦的地面，或者從塔上發(fā)射炮彈（y（0）≠0）

3.直接求解

最后，兩位科學(xué)家使用了積分來求解，事實(shí)證明問題并非如此困難。x和y的方程可以獨(dú)立求解。通過求解每個方程（并應(yīng)用初始條件）給出。

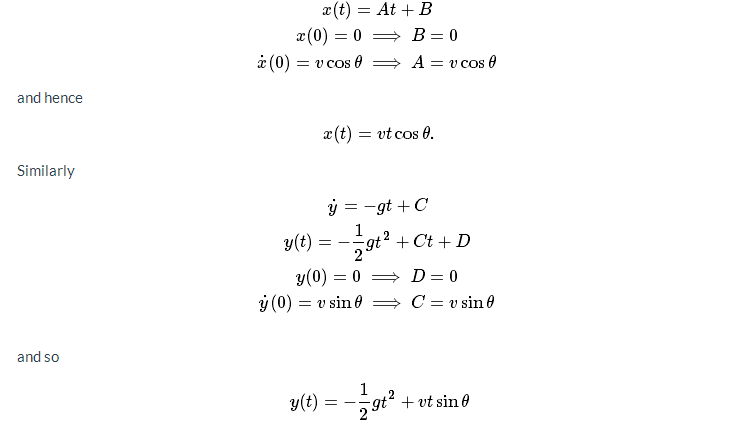
他們以x和y坐標(biāo)作為時間的函數(shù)。什么時候射彈擊中了地面呢？當(dāng)y=0時！即：

求解t*=0（大炮射擊之前），并求解t*=2vsinθg（當(dāng)它擊中地面時）。將第二個t*值插入到x的等式中，得到最終的行進(jìn)距離，等于：

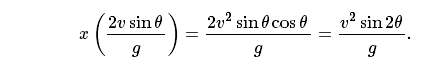
那么他們的最終預(yù)測模型就是

他們發(fā)現(xiàn)這與準(zhǔn)線性方法吻合。實(shí)際上，準(zhǔn)線性方法也給出了他們對引力常數(shù)的估計(jì)。

神經(jīng)常微分方程方法-學(xué)習(xí)動力系統(tǒng)

最后，假設(shè)他們不知道物理模型，只有一個常微分方程系統(tǒng)

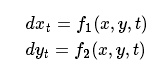
其中f1和f2是未知的（為簡潔起見省略虛擬變量）。

NIPS最近發(fā)表的一篇論文（https://papers.nips.cc/paper/7892-neural-ordinary-differential-equations）提出了一種學(xué)習(xí)常微分系統(tǒng)的方法。簡而言之，它通過用神經(jīng)網(wǎng)絡(luò)替換f1，f2并數(shù)值積分神經(jīng)網(wǎng)絡(luò)來獲得軌跡來實(shí)現(xiàn)這一點(diǎn)。學(xué)習(xí)可以正常進(jìn)行，因?yàn)閿?shù)值積分方法具有明確定義的梯度。在他們的例子中，如果科學(xué)家可以隨時間跟蹤炮彈的位置，即數(shù)據(jù)（xi，yi，ti），那么他們原則上可以恢復(fù)物理模型并了解物體隨著時間的推移而下降加速。這是一個令人興奮的深度學(xué)習(xí)新應(yīng)用，它開啟了學(xué)習(xí)系統(tǒng)行為的可能性，而不是簡單地學(xué)習(xí)它們的輸出。

我們學(xué)到了什么？

我們生活在一個幸運(yùn)的年代，可以通過數(shù)百種不同的方式解決一個簡單的問題。此外，在上述“黑盒”方法中，我們也可以將神經(jīng)網(wǎng)絡(luò)換成其他模型，并用上其他的優(yōu)化方法。這突出了機(jī)器學(xué)習(xí)在數(shù)學(xué)中的作用——它是我們用以理解世界和做出預(yù)測的許多強(qiáng)大工具之一。

數(shù)學(xué)家對數(shù)學(xué)模型是可解釋的，是直觀的，而深度學(xué)習(xí)模型正好相反。在我舉的例子中，構(gòu)建數(shù)學(xué)模型并用機(jī)器學(xué)習(xí)填補(bǔ)空白（比如估測引力常數(shù)）可以帶來更好的準(zhǔn)確性和更快的計(jì)算。

如果我們能夠盡可能多地融入物理理論，并利用機(jī)器學(xué)習(xí)來填補(bǔ)我們的知識空白，那么我們就有機(jī)會解決更復(fù)雜的問題。通常機(jī)器學(xué)習(xí)用于參數(shù)擬合，但在混合模型中，我們也可以用它來預(yù)測更復(fù)雜系統(tǒng)中的函數(shù)組成部分。

我相信，隨著理論和技術(shù)的進(jìn)步，我們將在未來看到許多混合模型。因此，數(shù)學(xué)建模和機(jī)器學(xué)習(xí)建模也應(yīng)當(dāng)是“合作關(guān)系”，而非“競爭關(guān)系”。