交流正弦波形是通過在磁場內旋轉線圈產生的,交流電壓和電流構成交流理論的基礎
直流或DC,因為它通常被稱為,是一種電流或電壓形式,僅在一個方向上繞電路流動,使其成為“單向”電源。
一般來說,直流電流和電壓都由電源,電池,發電機和太陽能電池產生,僅舉幾例。直流電壓或電流具有固定的幅度(幅度)和與之相關的確定方向。例如, + 12V 表示正方向為12伏,或 -5V 表示負方向為5伏。
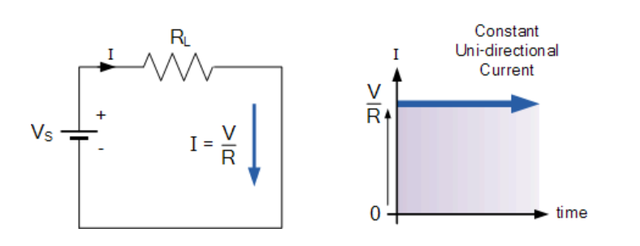
我們也知道DC電源在時間上不會改變它們的值,它們是在連續穩態方向上流動的恒定值。換句話說,DC始終保持相同的值,并且恒定的單向DC電源永遠不會改變或變為負值,除非它的連接是物理反轉的。簡單的直流或直流電路示例如下所示。
直流電路和波形

另一方面,交替函數或AC波形被定義為在大小和方向上或多或少均勻地相對于時間變化的一個,使其成為“雙向的” “波形。 AC功能可以表示具有 AC波形形狀的電源或信號源,通常遵循數學正弦曲線的形狀: A(t)= A max * sin(2π?t)。
術語AC或者給出它對交流電的完整描述,通常指的是時變波形,其中最常見的是被稱為正弦波更好地稱為正弦波形。正弦波形通常通過其簡短描述稱為正弦波。正弦波是目前電氣工程中最重要的交流波形之一。
通過繪制電壓或電流的瞬時縱坐標值得到的形狀稱為AC波形的。交流波形每隔半個周期不斷改變其極性,在正時間和正負最大值之間交替變化,其中一個例子就是我們在家中使用的國內電源電壓。
這意味著 AC波形是“時間相關信號”,其中最常見類型的時間相關信號是周期波形。周期性或交流波形是旋轉發電機的最終產品。通常,可以使用基頻生成任何周期性波形的形狀,并將其與不同頻率和幅度的諧波信號疊加,但這是另一個教程。
交流電壓和電流不能存儲在電池或像直流電(DC)這樣的電池可以在需要時使用交流發電機或波形發生器產生這些量更容易和更便宜。 AC波形的類型和形狀取決于產生它們的發生器或設備,但所有AC波形由零電壓線組成,該線將波形分成兩個對稱的半部。AC波形的主要特征定義為:
AC波形特征
?期間, (T)是波形從開始到結束重復自身所用的時間長度(以秒為單位)。這也可以稱為正弦波波形的周期時間,或方波的脈沖寬度。
?頻率,(?)是波形在一秒時間內重復的次數。頻率是時間段的倒數,(?= 1 / T ),頻率單位為赫茲,(Hz)。
?幅度(A)是以伏特或安培為單位測量的信號波形的幅度或強度。
在我們關于波形的教程中,我們研究了不同的類型波形并表示“波形基本上是繪制到時間基準的電壓或電流變化的直觀表示”。通常,對于AC波形,該水平基線表示電壓或電流的零條件。位于水平零軸上方的AC型波形的任何部分表示在一個方向上流動的電壓或電流。
同樣,位于水平零軸下方的波形的任何部分表示電壓或電流與第一個方向相反的方向流動。通常對于正弦AC波形,零軸上方的波形形狀與其下方的形狀相同。但是,對于包括音頻波形在內的大多數非功率交流信號,并非總是如此。
電氣和電子工程中最常用的周期性信號波形是正弦波形。然而,交替的AC波形可能不總是采用基于三角正弦或余弦函數的平滑形狀的形狀。交流波形也可以采用復波,方波或三角波的形狀,如下所示。
周期波形的類型

AC波形從正半部分到負半部分完成一個完整模式并再次返回零基線所需的時間稱為循環和一個完整循環包含正半循環和負半循環。波形完成一個完整周期所需的時間稱為波形的周期時間,并給出符號“T”。
完成周期的完整周期數在一秒(周期/秒)內產生的信號稱為交替波形的頻率,符號?。頻率以赫茲,( Hz )測量,以德國物理學家海因里希赫茲命名。
然后我們可以看到周期之間存在關系(振蕩) ),周期時間和頻率(每秒周期數),因此如果在一秒內有?個周期,則每個周期必須以 1 /?秒完成。
頻率與周期時間的關系
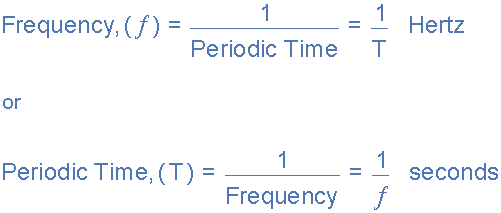
AC波形示例No1
1。什么是50Hz波形的周期時間和2.周期時間為10mS的交流波形的頻率是什么。
1。
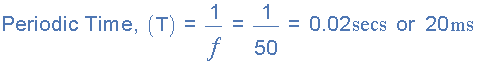
2)。
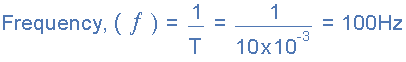
用于表示的頻率“每秒周期“縮寫為”cps“,但今天更常用”Hertz“單位指定。對于家用主電源,頻率將為50Hz或60Hz,具體取決于國家,并由發電機的旋轉速度確定。但是一個赫茲是一個非常小的單位,因此使用前綴來表示在較高頻率下波形的數量級,例如kHz,MHz甚至GHz.
頻率前綴的定義

除了知道交流量的周期時間或頻率外,交流波形的另一個重要參數是幅度,更好地稱為最大值或峰值,由電壓或 I max I max 表示的 V max EM>交流波形的幅度
峰值是波形在零基線測量的每個半周期內達到的電壓或電流的最大值。與具有可使用歐姆定律測量或計算的穩態的直流電壓或電流不同,交流量隨時間不斷變化其值。
對于純正弦波形,此峰值始終為兩個半周期( + Vm = -Vm )相同,但對于非正弦波或復雜波形,每個半周期的最大峰值可能非常不同。有時,交替波形給出峰峰值, V pp 值,這只是距離或電壓之和。最大峰值, + V max 以及一個完整周期內的最小峰值 -V max 。 / p>
AC波形的平均值
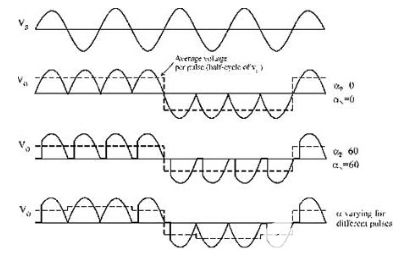
當DC電壓恒定時,連續DC電壓的平均值或平均值將始終等于其最大峰值。該平均值僅在DC電壓的占空比改變時才會改變。在純正弦波中,如果在整個周期內計算平均值,則平均值將等于零,因為正半部和負半部將相互抵消。因此,僅在半個周期內計算或測量AC波形的平均值或平均值,如下所示。
非正弦波形的平均值
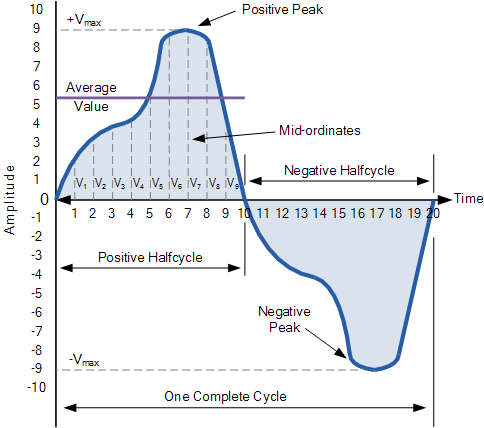
要找到我們需要的波形的平均值使用中坐標規則,梯形規則或數學中常見的辛普森規則來計算波形下方的面積。通過簡單地使用中坐標規則可以很容易地找到任何不規則波形下的近似面積。
零軸基線被分成任意數量的相等部分,在上面的簡單示例中,該值為9,(V 1 至V 9 )。繪制的縱坐標線越精確,將是最終平均值或平均值。平均值將是加在一起的所有瞬時值的相加,然后除以總數。如下所示。
AC波形的平均值
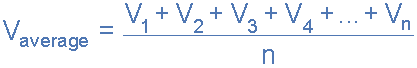
其中: n 等于實際使用的中間坐標數。
對于純正弦波形,此平均值或平均值始終等于 0.637 * V max 這種關系也適用于電流的平均值。
交流波形的RMS值
我們計算的交流波形的平均值為:0.637 * V max 與我們用于直流電源的值不同。這是因為與恒定且具有固定值的DC電源不同,AC波形隨時間不斷變化并且沒有固定值。因此,為負載提供與DC等效電路相同的電功率的交流系統的等效值稱為“有效值”。
正弦波的有效值產生相同的值I 2 *在負載中的R加熱效應,正如我們所預期的那樣,是否通過恒定DC電源供給相同的負載。正弦波的有效值通常稱為Root Mean Squared或簡稱RMS值,因為它被計算為平均值(平均值)的平方根。電壓或電流的平方。
即V rms 或I rms 給出所有的平均值的平方根平方正弦波的正中值。任何AC波形的RMS值可以從以下修改的平均值公式中找到,如圖所示。
AC波形的RMS值
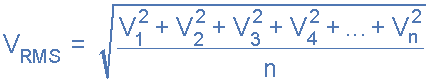
其中: n 等于中坐標數。
對于純正弦波形,此有效或RMS值也將始終相等: 1 / √ 2 * V max 等于 0.707 * V max ,此關系適用于當前的RMS值。除矩形波形外,正弦波形的RMS值始終大于平均值。在這種情況下,加熱效果保持不變,因此平均值和RMS值將相同。
關于R.M.S.的最后評論。值。除非另有說明,否則大多數萬用表(數字或模擬)僅測量R.M.S.電壓和電流的值而不是平均值。因此,在直流系統上使用萬用表時,讀數將等于 I = V / R ,對于交流系統,讀數將等于 Irms = Vrms / R 。
此外,除了平均功率計算,在計算RMS或峰值電壓時,僅使用V RMS 來查找I RMS 值,或者峰值電壓,Vp找到峰值電流,Ip值。不要將它們混合在一起,因為正弦波的RMS或峰值完全不同,您的結果肯定是不正確的。
形狀因子和波峰因數
雖然這些天很少使用,但形狀因子和波峰因數都可用于提供有關實際的信息AC波形的形狀。形狀因子是平均值和RMS值之間的比率,并給出為。

對于純正弦波形,Form Factor將始終等于 1.11 。波峰因數是R.M.S.之間的比率。值和波形的峰值,并給出為。

在純正弦波形中,波峰因數將始終等于 1.414 。
AC波形示例No2
6安培的正弦交流電流經過電阻為40Ω。計算電源的平均電壓和峰值電壓。
R.M.S.電壓值計算如下:
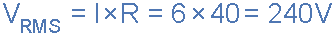
平均電壓值計算如下:

峰值電壓值計算如下:
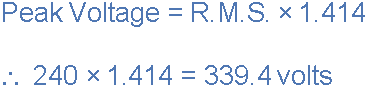
平均值,RMS,形狀因子和波峰因數的使用和計算也可以用于任何周期波形的類型,包括三角形,方形,鋸齒形或任何其他不規則或復雜的電壓/電流波形形狀。各種正弦值之間的轉換有時會令人困惑,因此下表提供了將一個正弦波值轉換為另一個正弦波值的便捷方法。
正弦波形轉換表

在下一篇關于正弦波形的教程中,我們將研究產生正弦交流波形(正弦曲線)及其角速度表示的原理。
-
電路
+關注
關注
172文章
5901瀏覽量
172134 -
頻率
+關注
關注
4文章
1494瀏覽量
59211 -
波形
+關注
關注
3文章
379瀏覽量
31544
發布評論請先 登錄
相關推薦




 交流波形電路理論和特征類型頻率案例及計算轉換
交流波形電路理論和特征類型頻率案例及計算轉換
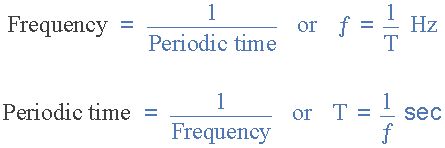











評論