布爾代數如何使用布爾代數定律減少數字門數的例子
布爾代數和布爾代數定律可用于識別數字邏輯設計中不必要的邏輯門減少功耗和成本所需的門數。
我們在本節中已經看到,數字邏輯功能可以定義并顯示為布爾代數表達式或邏輯門真值表。所以這里有一些例子說明我們如何使用布爾代數來簡化更大的數字邏輯電路。
布爾代數示例No1
構造一個真值表以下電路中 C , D 和 Q 點的邏輯功能,并確定可用于替換整個電路的單個邏輯門。
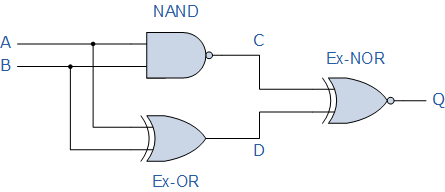
首先觀察告訴我們該電路由2輸入 NAND 門,2輸入 EX-OR 門,最后輸出端為2輸入 EX-NOR 門。由于標記 A 和 B 的電路只有2個輸入,因此輸入只能有4種可能的組合(2 2 )和它們是: 0-0 , 0-1 , 1-0 ,最后 1-1 。以表格形式繪制每個門的邏輯函數將為下面的整個邏輯電路提供以下真值表。
從上面的真值表中,列 C 表示由 NAND 門生成的輸出函數,而列 D 表示輸出函數來自 Ex-OR 門。這兩個輸出表達式都將成為輸出端 Ex-NOR 門的輸入條件。
從真值表中可以看出的輸出當 A 或 B 中的任何一個輸入處于邏輯 1 時,存在Q 。滿足此條件的唯一真值表是 OR 門。因此,整個上述電路只能用一個2輸入OR 門代替。
布爾代數示例No2
找到以下系統的布爾代數表達式。

系統由組成AND 門, NOR 門,最后是 OR 門。 AND 門的表達式為 A.B , NOR 門的表達式為 A + B 。這兩個表達式也是 OR 門的單獨輸入,定義為 A + B 。因此,最終輸出表達式如下:

系統的輸出為 Q =(AB) +( A + B ),但符號 A + B 與De Morgan的符號 A 。 B 相同,然后替換 A 。 B 到輸出表達式給出了 Q =(AB)+( A 。 B )的最終輸出符號,這是 Exclusive-NOR 門的布爾表示法,如上一節所示。
| 輸入 | 輸出 | |||
| A | B | C | D | Q |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 輸入 | 中間體 | 輸出 | ||
| B | A | AB | A + B | Q |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
然后,上面的整個電路可以只用一個 Exclusive-NOR 門代替,實際上 Exclusive-NOR 門由這些單獨的門組成函數。
布爾代數示例No3
查找以下系統的布爾代數表達式。

這個系統可能看起來比其他兩個系統要復雜得多,但邏輯電路只包含簡單的 AND , OR 和 NOT 連接在一起的門。
與前面的布爾示例一樣,我們可以通過依次寫下每個邏輯門功能的布爾符號來簡化電路為了給出 Q 輸出的最終表達式。

當ALL門輸入在邏輯電平“1”處為高電平時,3輸入 AND 門的輸出僅為邏輯“1”( ABC )。當一個或兩個輸入 B 或 C 處于邏輯電平“0”時,低 OR 門的輸出僅為“1”。當輸入 A 為“1”且輸入 B 或時,2輸入 AND 門的輸出為“1” C 為“0”。當輸入 ABC 等于“1”或 A 等于“1”并且兩個輸入時, Q 的輸出僅為“1” B 或 C 等于“0”, A.( B + C )。
使用“de Morgan定理”輸入 B 并輸入 C 取消,以便在 Q 處產生輸出,它們可以是邏輯“1”或邏輯“0”。然后,這只是輸入 A 作為在 Q 輸出所需的唯一輸入,如下表所示。
| 輸入 | 中間體 | 輸出 | ||||||
| C | B | A | ABC | B | C | B + C | A。( B + C ) | Q |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
然后我們可以看到上面的整個邏輯電路只能被標記為“ A ”的單個輸入所取代,從而將六個獨立邏輯門的電路減少到只有一根電線,(或緩沖器) 。使用布爾代數的這種類型的電路分析可以非常強大并且可以快速識別數字邏輯設計中的任何不必要的邏輯門,從而減少所需的門數,電路的功耗以及成本
-
布爾代數
+關注
關注
0文章
10瀏覽量
7875 -
數字邏輯
+關注
關注
0文章
73瀏覽量
16664
發布評論請先 登錄
相關推薦
邏輯代數基礎
正反轉布爾,自動控制布爾,控制量這三個控件是從哪里來
三個小數求和,判斷等于1?為什么有的值行,有的值不行
求助:我想編寫一個三個布爾輸入控件,我想輸入000的時候,輸出1。
關于代數攻擊中代數免疫的若干性質分析
邏輯代數的基本定律和規則
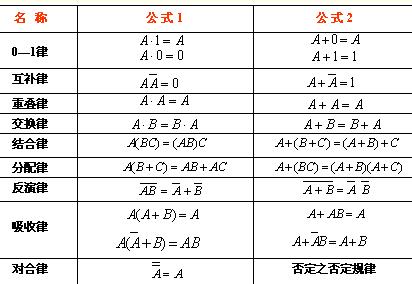




 三個布爾代數示例說明
三個布爾代數示例說明










評論