當負載的電阻值等于電壓源內部電阻的值，允許提供最大功率時，發生最大功率傳輸，通常，此源電阻甚至阻抗如果涉及電感器或電容器具有歐姆的固定值。

然而，當我們連接負載電阻時， R L 穿過在電源的輸出端子中，負載的阻抗將從開路狀態變化到短路狀態，導致負載吸收的功率變得依賴于實際電源的阻抗。然后，為了使負載電阻能夠吸收可能的最大功率，它必須與電源的阻抗“匹配”，這構成了最大功率傳輸的基礎。

最大功率傳輸定理是另一種有用的電路分析方法，用于確保當負載電阻值恰好等于電源電阻時，最大功率消耗將在負載電阻中消耗。負載阻抗與能量源的內部阻抗之間的關系將給出負載中的功率。考慮下面的電路。

Thevenins等效電路

在上面的戴維寧等效電路中，最大功率傳遞定理表明，“如果它與提供功率的網絡的Thevenin或Norton源電阻的值相等，則負載電阻中的最大功率消耗將消耗。” / p>

換句話說，導致最大功耗的負載電阻必須等于相當于戴維寧源電阻的值，然后 R L = R S 但如果負載電阻值低于或高于網絡的戴維寧源電阻，則其耗散功率將小于最大值。

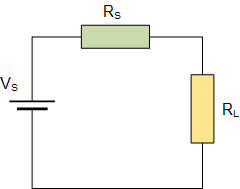
例如，找到值負載電阻 R L 將在以下電路中提供最大功率傳輸。

最大功率傳輸示例No1

然后使用以下方法歐姆定律方程：

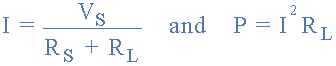
我們現在可以完成下表來確定電路中不同負載電阻值的電流和功率。

電流對表

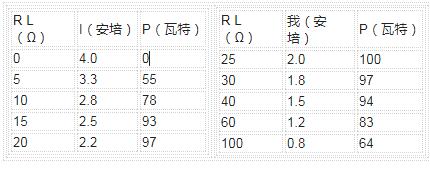
使用上表中的數據，我們可以繪制一個負載圖對于不同的負載電阻值，電阻 R L ， P 。另請注意，開路時功率為零（零電流）條件）以及短路（零電壓條件）。

電源負載電阻圖

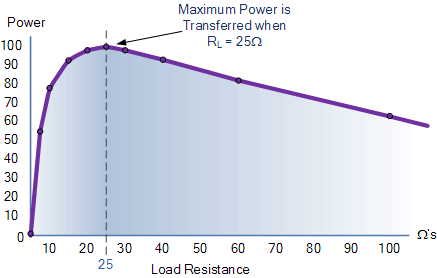
從上表和圖表中可以看出，當負載電阻 R L <時，負載中出現最大功率傳輸/ span>的值與源電阻相等， R S ： R S = R L =25Ω。這被稱為“匹配條件”，并且作為一般規則，當外部設備的阻抗時，最大功率從諸如電源或電池的有源設備傳輸到外部設備。完全匹配源的阻抗。

一個很好的例子阻抗匹配的le在音頻放大器和揚聲器之間。放大器的輸出阻抗 Z OUT 可以在4Ω和8Ω之間給出，而標稱輸入揚聲器的阻抗 Z IN 可能僅為8Ω。

然后，如果8Ω揚聲器連接到放大器輸出端，放大器將把揚聲器視為8Ω負載。并聯兩個8Ω揚聲器相當于驅動一個4Ω揚聲器的放大器，兩種配置均在放大器的輸出規格范圍內。

阻抗不當匹配會導致過多的功率損耗和散熱。但是，如何阻抗匹配具有非常不同阻抗的放大器和揚聲器。那么，有可用的揚聲器阻抗匹配變壓器，可以將阻抗從4Ω改變到8Ω，或者16Ω，以允許連接的許多揚聲器的阻抗匹配各種組合，例如PA（公共廣播）系統。

變壓器阻抗匹配

阻抗匹配的一個非常有用的應用，以便在信號源和信號源之間提供最大的功率傳輸。負載處于放大器電路的輸出級。信號變壓器用于將揚聲器的較高或較低阻抗值與放大器輸出阻抗相匹配，以獲得最大聲功率輸出。這些音頻信號變壓器稱為“匹配變壓器”，并將負載耦合到放大器輸出，如下所示。

變壓器阻抗匹配

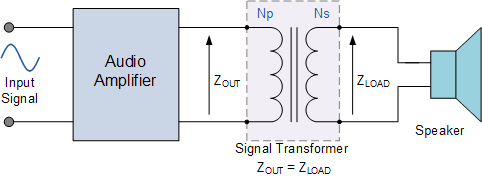
即使輸出阻抗與負載阻抗不同，也可以獲得最大功率傳輸。這可以通過變壓器上合適的“匝數比”來實現，相應的負載阻抗比率 Z LOAD 與輸出阻抗， Z OUT 匹配變壓器初級匝數與次級匝數之比，因為變壓器一側的電阻變為另一側的不同值。

如果負載阻抗， Z LOAD 是純電阻性的，源阻抗是純電阻性的， Z OUT 然后找到最大值的等式權力轉移如下：

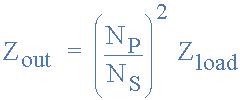
其中： N P 是初級匝數和 N S 變壓器上的次級匝數。然后，通過改變變壓器匝數比的值，輸出阻抗可以與源阻抗“匹配”，以實現最大功率傳輸。例如，

最大功率傳輸示例No2

如果要將8Ω揚聲器連接到輸出阻抗1000Ω<的放大器/ span>，計算提供音頻信號最大功率傳輸所需的匹配變壓器的匝數比。假設放大器源阻抗 Z 1 ，負載阻抗 Z 2 ，匝數比為<跨度>名詞

通常，低功率放大器電路中使用的小型高頻音頻變壓器幾乎總是被認為是簡單的理想選擇，因此可以忽略任何損耗。