電機作為一種重要的驅動設備,尤其三相電機,在日常生活以及工業之中有著極為廣泛的運用,引起了越來越多的人的關注和重視。然而基于三相電機本身具有的特點,其使用環境復雜多樣,在這樣的情況下,使得在運轉過程中,常常出現各種意想不到的問題,給正常的生產經營帶來諸多的問題和困難,對設備的性能造成了不可逆的破壞,同時還極可能造成各種危險和事故。面對這樣的情況,電機的故障診斷技術和方法得到了迅速發展。
目前,電機故障診斷的方法較多,如神經網絡、專家學習、深度學習等。但基于電壓電流的診斷是工程實施最方便的方法,而用于電機故障診斷的電壓電流數據是需要電流電壓的波形數據,這必然就涉及到電流電壓的采集以及數據分析。
本文主要介紹電流電壓數據采集和電量計算方面的主要技術方法。
電壓電流波形采集
工業現場中的電流電壓信號是模擬量數據,都是隨時間連續變化的,稱為連續信號。但對于計算機來說,處理這些連續的信號顯然是無能為力,要使計算機能夠識別、計算、處理這些連續信號就必須將其轉化為離散信號,將連續信號轉換為離散信號的過程就叫采樣。因此,要分析電流電壓的數據,需要模擬量的電流電壓數據進行性采樣。在模擬量采集領域,必然遵循采樣定理,而最重要也是基本的采樣定理便是香農采樣定理。
1香農采樣定理
香農采樣定理,又稱內奎斯特采樣定理,是美國物理學家內奎斯特于1924年提出的一個理論。該理論是信息論,特別是通訊與信號處理學科中的一個重要的基本結論。
香農采樣定理定義:
為了不失真地恢復模擬信號,采樣頻率應該不小于模擬頻譜中最高頻率的2倍,即:
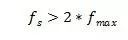
我們可以同構不同速率測量的正弦波來理解其原因
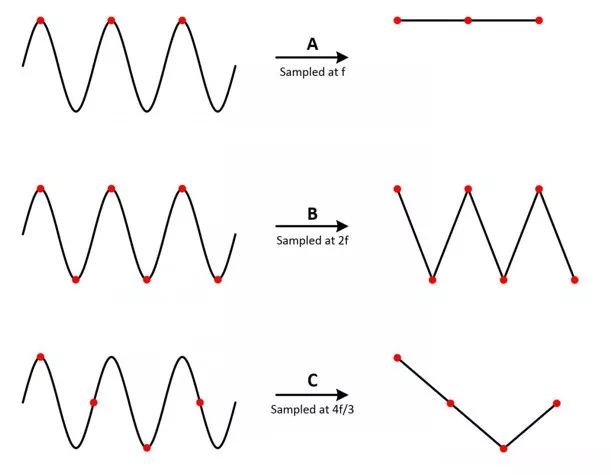
圖1采樣率過低的波形重構圖
情況A,頻率f的正弦波以同一頻率采樣,這些采樣標記在原始信號的左側,在右側構建時,信號錯誤地顯示為恒定直流電壓。
情況B,采樣率是信號頻率的兩倍。現在信號顯示為三角波。這種情況下,f等于奈奎斯特頻率,這也是特定采樣頻率下為了避免混疊而允許的最高頻率分量。
情況C,采樣率是4f/3。此時重構的波形無法準確的還原原波形信號。
可見,采樣率過低會造成波形重構不準確。因此,為了無失真地恢復原波形信號,采樣率fs必須大于被測信號感興趣最高頻率分量的兩倍。通常希望采樣率大于信號頻率約五倍。
2UIM采樣電路
公司研發的電壓電流采集終端UIM實現了電機運行時電流電壓數據的采集、轉換和分析,具有采集精度高,傳輸數據量大,支持信號類型多,運行穩定等優點。目前已在造紙行業、煤機行業、電機制造業、水泥行業等場合得到了應用。
電壓電流采集終端使用了模擬轉換芯片ADS1258進行模擬信號的采集和轉換。
電量參數計算
電機電量參數包含功率因數、有功功率、無功功率、電壓RMS、電流RMS、電壓不平衡、電流不平衡、負載率、頻率、總諧波率等。
電量參數均是由電流電壓的波形數據計算而來。其中電壓RMS可根據實時監測的電壓波形數據進行線電壓和相電壓的轉換以及積分求得,同理電流RMS也可以用同樣的方法得到;電壓不平衡度、電流不平衡度、負載率、總諧波率的計算也比較簡單;而有功功率和頻率的計算稍微復雜,下面主要介紹有功功率和頻率的計算方法。
1有功功率測量方法
在三相電路的功率測量中,主要測量方法有二瓦計法和三瓦記法兩種方法。
二瓦計法的理論依據是基爾霍夫電流定律,適用于在三相回路中只有三個電流存在的場合,如:a、三相三線制接法,中線不引出(只能采用二瓦計法);b、三相三線制,中線引出但不與地線或實驗電源相連的場合。
三瓦計法由于需要采用中性點作為電壓的參考點,因此該方法適用的場合如:a、三相三線制,中性線引出,但中性線不與電源或地線連接的場合;b、三相四線制,由于無法判斷三相負載是否平衡或是否中性線上有零序電流產生,只能采用三瓦計法。
可見,對于不同的接線方式場合,應選擇合適的功率測量方式,才能得到準確的功率參數。目前,已經部署UIM的工業現場采用的電壓互感器為三相三線制,并且沒有引出中性線,從電壓傳感器出來的信號是表示三相電機的線電壓,從電流互感器出來的信號是表示電機的三相電流信號。因此,采用的功率測量方法是二瓦計法。
二瓦計法的理論依據是基爾霍夫電流定律:在集總電路中,任何時刻,對任意節點,所有流入流出節點的之旅電流的代數和恒等于零。
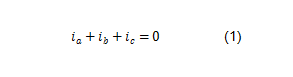
假設三相負載的中線為N,依據電壓的定義:
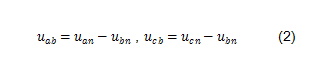
三相瞬時功率:
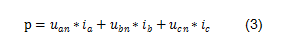
將式(1)和式(2)代入式(3),得
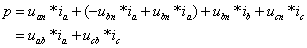
因此,有功功率等于瞬時功率在一個周期內求積分再求平均,得到:
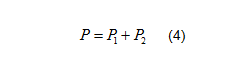
P為三相電路有功功率的總和,為在一個周期內的積分的平均值,為在一個周期內的平均值。在正弦穩態電路中:
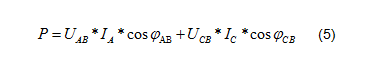
即: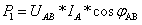
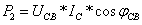 式中,
式中,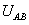
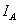
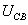
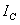 均為正弦電壓電流的有效值;
均為正弦電壓電流的有效值;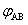 為
為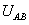 和
和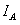 的相位差。
的相位差。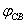 為
為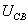 和
和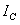 的相位差。
的相位差。
從變換的公式中可以看出,采用這種方法進行三相總功率測量時,只需要測量兩個電壓和兩個電流,這就是二瓦計法的推導原理及由來。
2頻率計算——FFT
工頻50Hz下的電壓電流波形中包含有若干頻率的雜波,根據波形數據計算出電壓電流的頻率,目前常用的是快速傅里葉變換(FFT)。
快速傅里葉變換(fastFouriertransform)是1965年由J.W.庫利和T.W.圖基提出的,是根據離散傅氏變換的奇、偶、虛、實等特性,對離散傅立葉變換的算法進行改進獲得的,簡稱FFT。
FFT的基本思想是把原始的N點序列,依次分解成一系列的短序列。充分利用DFT計算式中指數因子所具有的對稱性質和周期性質,進而求出這些短序列相應的DFT并進行適當組合,達到刪除重復計算,減少乘法運算和簡化結構的目的。特別是被變換的抽樣點數N越多,FFT算法計算量的節省就越顯著。下面對FFT和DFT的計算量進行了簡要對比分析。
有限長離散信號x(n),n=0,1,…,N-1的DFT定義為:
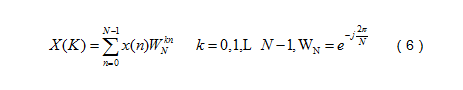
可以看出,DFT需要計算大約N2次乘法和N2次加法。當N較大時,這個計算量是很大的。利用WN的對稱性和周期性,將N點DFT分解為兩個N/2點的DFT,這樣兩個N/2點DFT總的計算量只是原來的一半,即(N/2)2+(N/2)2=N2/2,這樣可以繼續分解下去,將N/2再分解為N/4點DFT等。對于N=2m點的DFT都可以分解為2點的DFT,這樣其計算量可以減少為(N/2)log2N次乘法和Nlog2N次加法。
下面簡要介紹FFT的基本思路:

其中X1(k)和X2(k)分別為x1(n)和x2(n)的N/2點DFT。由于X1(k)和X2(k)均以N/2為周期,且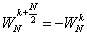 ,所以X(k)又可表示為:
,所以X(k)又可表示為:
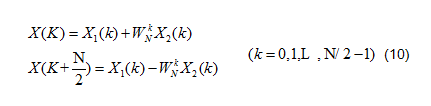
上式的運算可以用圖2表示,根據其形狀稱之為蝶形運算。依此類推,經過m-1次分解,最后將N點DFT分解為N/2個兩點DFT。
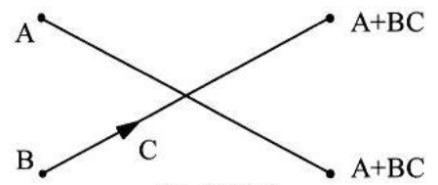
圖2FFT的蝶行運算
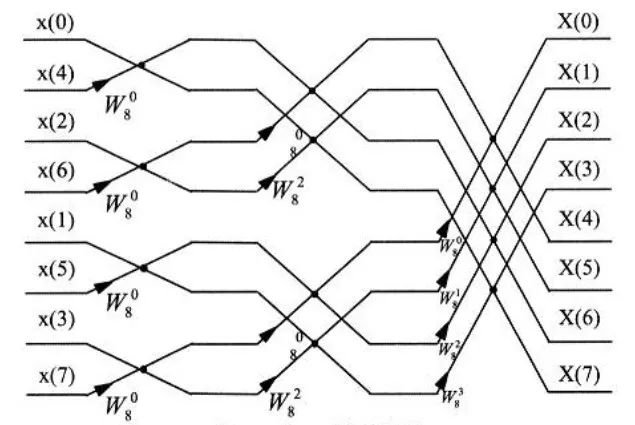
圖38點FFT分解流程圖
結束語
上面簡單講述了進行電壓電流數據采集時使用到的原理,以及進行電量參數計算所用到的計算方法的基本思想,希望通過上述的閱讀,能夠對數據采集和電量參數計算有所基本了解,以便更好地交流或學習。
-
神經網絡
+關注
關注
42文章
4789瀏覽量
101528 -
電壓
+關注
關注
45文章
5652瀏覽量
116603
原文標題:電壓電流采集技術——數據采集和電量參數計算
文章出處:【微信號:ljdj6900,微信公眾號:力久電機】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦

數據采集模塊類型與應用
PLC數據采集模塊的故障排除技巧

邊緣計算物聯網關如何優化數據采集?
天拓四方:邊緣計算網關在機床數據采集中的應用





 電壓電流采集技術——數據采集和電量參數計算
電壓電流采集技術——數據采集和電量參數計算













評論