今天的文章介紹了1900年前的數學發展史。過去100年來,數學有了很大的發展,除了像微分方程和微分幾何這些與經典物理本身有深刻關系的數學以外,還發展出了代數拓撲、代數幾何、代數數論、范疇學、幾何表示論等極度抽象的數學。而近代數學不是一個僅僅關于“數”的學問。以范疇學為代表的近代數學,更是一門關于關系和結構的抽象學問。有趣的是,近年來,這些看似和現實毫無關系的數學理論,特別是代數拓撲、代數幾何和范疇學已經開始和現代物理深度碰撞。
1
物理學革命與數學的引入
歷史上物理和數學有著十分深刻的聯系。物理的目的之一是了解新的自然現象。而一個新的自然現象之所以新的標志,就是我們連描寫它的名字及數學符號都沒有。這就是為什么當物理學家有一個真正的新發現時,他/她什么都說不出來,什么都寫不出來,也無法進行計算推導。這時候就需要引入新的數學語言來描寫新的自然現象。這就是數學和物理之間的深刻聯系。正因為如此,每一次物理學的重大革命,其標志都是有新的數學被引入到物理學中來。
第一次物理革命是力學革命,需要研究的物理現象是天體的的運動。牛頓不僅要發明他的萬有引力理論,而且還要發明微積分這一套新的數學來描寫他的理論。第二次物理革命是電磁革命。麥克斯韋發現了一種新的物質形態——場形態物質。這就是電磁波,也是光波。后來人們發現,這種場形態物質需要用數學的纖維叢理論來描寫。第三次物理革命是廣義相對論。愛因斯坦發現了第二種場形態物質——引力波。他需要引入數學中的黎曼幾何來描寫這種新物質。第四次物理革命是量子革命。這次革命揭示出,我們世界中的真實存在,既不是粒子也不是波,但既是粒子又是波。這種莫名其妙卻又真實的存在,可以用量子力學來解釋,而量子力學則是建立在數學中的線性代數理論之上。
牛頓、麥克斯韋、黎曼、愛因斯坦
我們現在正在經歷一場新的物理革命——第二次量子革命。這次革命的主角是量子信息和它們的量子糾纏。這次我們所遇到的新現象,就是很多很多量子比特的糾纏。這種多體量子糾纏的內部結構,正是我們既說不出來,又沒有名字的新現象。我們現在正在發展一套新的數學理論(某種形式的范疇學),來試圖描寫這種新現象。
這次正在進行中的物理學新革命是非常深刻的。因為這次革命試圖用糾纏的量子信息來統一所有的物質、所有的基本粒子、所有的相互作用,甚至時空本身。而凝聚態物理中的拓撲序、拓撲物態,以及量子計算中的拓撲量子計算,都是多體量子糾纏的應用。正是通過這些物理研究,我們發現了多體量子糾纏的重要性,并引入了長程量子糾纏這一相關概念。
2
用數學的眼光看物理學
我們剛才用物理的眼光,概括了數學和物理的關系。自牛頓以來,我們都是用分析的眼光看世界,用連續流形、連續場來描寫物理現象。特別是愛因斯坦的廣義相對論,它是如此的漂亮自然,大家都認為它抓住了宇宙的本質。之后,以幾何的眼光看世界成為物理的主流。在這個思路下,物理學家發展了規范場論、量子場論,以及描寫所有基本粒子的標準模型。
但完美主流的幾何的眼光,并不一定是認識世界的正確方法。從量子革命以來,我們越來越意識到,我們的世界不是連續的,而是離散的。我們應該用代數的眼光看世界。連續的分析,僅僅是離散的代數的一個幻象。就像連續的流體,是許許多多一個個分子集體運動的幻象。這種以代數的眼光看世界的新思想,將顛覆很多目前的主流物理理論,帶來物理的第二次量子革命。某種意義上,建立在幾何思路之上的廣義相對論、規范場論、量子場論太漂亮太完美了,讓我們誤以為它抓住了宇宙的本質,誤導了我們一百多年。
有趣的是,這100多年來,近代數學發展的一條脈絡也正是從連續到離散、從分析到代數的脈絡,也提出了離散的代數是比連續的分析更本質的觀點。60年代由Grothendieck學派發展出來的代數幾何理論正是這種思想的代表,代數幾何可以看作是實現了連續和離散的統一的幾何理論。這和物理學從經典到量子的發展一一相映。而實現統一的語言當然是代數的,更準確的說,是一個超越了集合論的、全新的數學語言,也是代數幾何的基礎語言:范疇學。
40年代Eilenberg和Mac Lane發展了范疇學,60年代Grothendieck在此基礎上發展了代數幾何。
3
范疇學的精神
下面讓我從一個外行的角度,來粗略介紹一下范疇學的精神。通常,如果我們想要深入了解一個物體,我們會把這個物體分解成越來越小、越來越簡單的構件。如果我們可以做到這一點,我們就認為了解了這個物體。這一思想方法就是還原論的思路。這是科學思想方法的一個主流。很多人甚至用它來定義什么叫做“理解”。
但主流并不代表正確。“理解”也可以由另外一種完全不同的方式來實現。我們不試圖把物體分成更小更簡單的基本構件。我們甚至不去考慮物體的內部結構,也許物體根本就沒有什么內部結構。我們試圖通過這個物體和其他所有物體的關系和作用,來了解這個物體。
其實,和其他物體的關系和作用,正代表了這個物體所有可能的性質。而一個物體的所有可能性質,也就完全定義了這個物體本身。歸根到底,也許我們根本就沒有物體,只有一大堆關系。而物體這一抽象的概念,以及物體所有可能的性質,是由這一堆關系來定義的。這就是范疇學的精神。
把這一范疇學的思路應用到認識論,我們發現所謂的“客觀存在”,其實是人腦通過觀察到的大量的、各種各樣的關系,所抽象出來的一個概念。也就是說,我們頭腦中的主觀印象觀察是客觀的。而所謂的“客觀存在”,反而是主觀的。因為我們所觀察到的大量的、各種各樣的關系不是隨機混亂的,這些關系之間有非常強烈的關聯。這些強烈的關聯賦予我們“客觀存在”這一想象(或概念)。吳詠時老師舉過一個社會學例子:范疇學的精神正像馬克思說過的,人這個個體是通過人和人的關系定義的。所以范疇學是關系學,也是認識世界的一種新方式。
01
我們也可以把范疇學的思路用到物理中對相和相變的理解。兩個相之間的相變,就是范疇學中的“關系”。而相這個概念,就是通過所有相變(即“關系”)來定義的。
02
物理學中的第2個例子是量子力學理論。通過量子力學中的波函數來理解我們的量子世界,其實是一種還原論的思路。如果我們要用范疇學的思路來理解我們的量子世界,那我們將像實驗物理學家一樣,直接考慮各種各樣的觀測(這些觀測對應于我們上面說的關系),而且我們只考慮各種各樣的觀測。這些觀測(關系)之間有很強的關聯。通過這些關系之間的關系,我們可以直接理解我們的量子世界。這就是范疇學的思路。
現有的量子理論用的不是這一思路,而是通過對觀測之間的關系的總結,抽象出波函數這一概念,代表所謂的“客觀存在”。然后我們再通過波函數來理解我們的量子世界。
其實波函數(及其背后的線性代數),僅僅是我們對現有實驗觀測的一個模型。這一模型不見得唯一,也就是說,可能有另一個理論可以同樣有效地描寫我們的量子世界。這一模型也不見得正確,也許將來新的實驗觀測會和現有的模型矛盾。這將迫使我們構造一個新的模型,也就是發展一套新的理論,來描寫我們的量子世界。
其實用范疇學的思路來理解我們的量子世界,就是要放棄波函數這一概念。這將有助于我們不受波函數的束縛,來進一步發展量子力學。
03
物理學中第3個例子,就是具有長程糾纏的量子物態。量子物態中的組分有可能有長程糾纏。這些長程糾纏的各種各樣的構型,會給出各種各樣不同的量子物態[1]。這就是量子物態中所謂的拓撲序(見《拓撲序:看世界的一種新視角 | 眾妙之門》)。有長程糾纏的量子物態,是一類全新的物態,有各種想以前想不到的新現象。
陳諧(左)顧正澄(右)和我在一系列工作中提出了長程糾纏和對稱保護序的概念,并發展了對稱保護序的上同調理論。
長程量子糾纏及其對應的拓撲序,是一個全新的自然現象。我們到底應該用什么樣的數學來描寫這一新現象?近十幾年來的研究發現,張量范疇學和高階范疇學正是描寫長程糾纏(拓撲序)的數學框架。其實拓撲序物態中的拓撲準粒子對應于范疇學中的“實體”(object,即所謂的“客觀存在”),而準粒子的交換、融合等操作,對應于范疇學中的關系(morphism)。張量范疇學正巧是描寫拓撲準粒子的完備理論。它可描寫拓撲序物態中的拓撲準粒子所具有的各種非常新奇的性質,如分數電荷、分數自由度、分數統計,甚至是非阿貝爾統計,等等。正是這些新奇的性質(非阿貝爾統計),使我們可以用拓撲物態進行拓撲量子計算。
吳詠時(左)指出分數統計(準粒子的交換操作)的數學基礎是編織群表示。王正漢(右)及其合作者對簡單的模張量范疇進行了完全分類。
通過范疇學,我們得到了對拓撲序(即長程糾纏)的全面理解和分類。比如在1維,沒有非平凡的拓撲序,也就是說沒有長程糾纏,只有短程糾纏。在二維,各種各樣的拓撲序可以由一類特殊的張量范疇——模張量范疇——來一一描寫[2]。在三維,各種各樣的拓撲序可以由一類特殊的融合二階范疇來一一描寫[3]。
蘭天(左)、孔良(中)、朱晨暢(右)和我的一系列工作對三維拓撲序進行了完全的分類和構建。
4
代數拓撲在凝聚態物理中的應用
近代數學的另一重要分支——代數拓撲,也在凝聚態物理中有重要的應用。上面提到長程糾纏(即拓撲序)代表了一類新型的量子物態。那么長程糾纏的反面——短程糾纏,應當只能描寫那些平庸的、沒意思的量子物態。可最近十幾年的研究揭示,如果系統有對稱性,那么即使是沒有拓撲序的短程糾纏的量子物態,也可以是非平凡的。這類非平凡短程糾纏態被稱之為“對稱保護序”。媒體中常說的拓撲絕緣體[4],就是一種沒有拓撲序,但有對稱保護序的量子物態。雖然有短程糾纏的對稱保護序,沒有分數電荷,沒有分數自由度,也沒有分數統計,但它們會有非平凡的、可以導電導熱的邊界,這使之成為目前凝聚態物理研究的一個大熱點。
Mele(左)和Kane(右)在理論上發現了拓撲絕緣體
而代數拓撲中的上同調理論和示性類理論,正是描寫這些短程糾纏(即對稱保護序)的數學語言。這些代數拓撲理論使我們對一維有能隙的物態有了完全的理解和分類[5],也使我們對高維的對稱保護序有了完全的理解和分類[6]。
有很長一段時間,我們認為所有的物態都可以通過朗道的對稱性和對稱性破缺理論來理解。為了理解這些物態,為了研究對稱性,很多物理學生都學群論。現在我們意識到,還有很多新的物態是超越朗道對稱性理論的。為了研究這些新的量子物態及其中的多體量子糾纏,今后許多物理學生,很可能還要學習范疇學和代數拓撲。(其實目前已經有很多物理學生開始學習范疇學、代數拓撲等現代數學理論)。這顯示了數學物理的交融和并肩發展。新的數學進入物理,也意味著物理目前正在進行一場改朝換代的新革命。
-
幾何
+關注
關注
0文章
37瀏覽量
12490 -
量子
+關注
關注
0文章
489瀏覽量
25756 -
電磁波
+關注
關注
21文章
1478瀏覽量
54439
原文標題:物理學的新革命——凝聚態物理中的近代數學
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
2024年諾貝爾物理學獎為何要頒給機器學習?
《實用模擬電路設計》[美 湯普森]
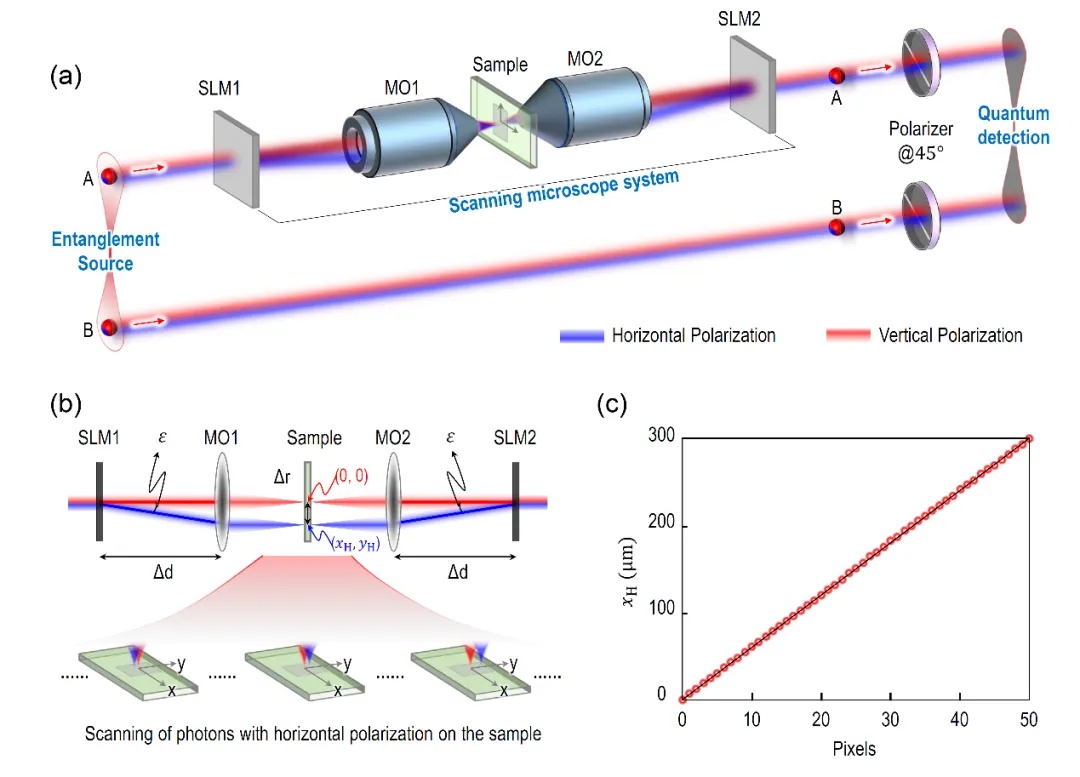
北京理工大學在量子顯微成像方面取得重要進展,實現量子全息顯微
鎖相放大器在物理學中的應用

神經網絡理論研究的物理學思想介紹
NVIDIA發布Cosmos?平臺,助力物理AI系統發展
無所不能的MATLAB|證明曲速引擎的物理學原理

《算力芯片 高性能 CPUGPUNPU 微架構分析》第3篇閱讀心得:GPU革命:從圖形引擎到AI加速器的蛻變
NVIDIA 助力谷歌量子 AI 通過量子器件物理學模擬加快處理器設計

云知聲如何迎接大模型2.0時代
AI產業革命的演進路徑與未來展望
NVIDIA為AI城市挑戰賽構建合成數據集
玩出夢想科技推出革命性安卓系統空間計算機MR
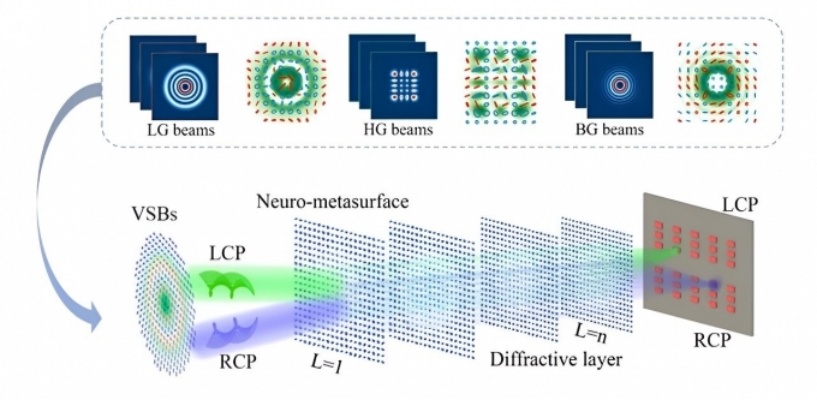
更精確操縱光束:新型超表面設計推動光學物理學發展


















評論