本文介紹的內容主要聚焦Google 的一項最新工作：改變基于 GEMM 實現的 CNN底層算法提出的新方法。通用矩陣乘法（General Matrix Multiply, GEMM）是廣泛用于線性代數、機器學習、統(tǒng)計學等各個領域的常見底層算法，其實現了基本的矩陣與矩陣相乘的功能，因此算法效率直接決定了所有上層模型性能，目前主流的卷積算法都是基于GEMM來實現的。來自谷歌的Peter Vajda在ECV2019中提出了一種全新的間接卷積算法，用于改進GEMM在實現卷積操作時存在的一些缺點，進而提升計算效率。

通用矩陣乘法

GEMM是基礎線性代數子程序庫（Basic Linear Algebra Subprograms, BLAS）中的一個函數。BLAS提供了實現矩陣和向量基本運算的函數，最早于1979年由C.L.LAWSON提出。BLAS的發(fā)展大致可以分為三個階段（levels）的歷程，這和函數定義，出版順序，以及算法中多項式的階數以及復雜性有關，第一階段只包含與向量（vector）有關的運算，第二階段添加了向量與矩陣進行運算的操作，第三階段添加了矩陣與矩陣之間的運算，前兩個階段的BLAS都是用于向量處理器的，而第三階段適用于矩陣處理器，所以BLAS的發(fā)展和硬件的發(fā)展密不可分。GEMM屬于第三階段的算法，正式公布于1990年，其迭代更新形式為：

其中A和B可以進行轉置或hermitian共軛轉置，而A、B和C都可以被忽略（be strided），因此實際上這個公式就表示了任意矩陣之間所有可能的加法和乘法組合，例如最基本的A*B，可以將α置1，C置為全0矩陣即可，這也是其通用性的表現。

由于矩陣乘法相對于向量-向量乘法以及向量-矩陣乘法，有更低的時間復雜度，效率更高，因此其廣泛用于許多科學任務中，與之相關的GEMM算法成為了目前BLAS設計者的主要優(yōu)化對象。例如可以將A和B分解為分塊矩陣，使得GEMM可以遞歸實現。有關GEMM的詳細信息可以參見[1][2][3]。如何對GEMM進行優(yōu)化，是BLAS相關工作的研究熱點。

基于 GEMM 的卷積算法及其缺點

卷積神經網絡（CNN）在CV問題中的表現很出色，有多種在算法層面對齊進行實現的方法：直接卷積算法，采用7層循環(huán)，快速卷積算法，利用傅里葉變換來進行卷積，以及基于GEMM的卷積算法。

通過將卷積操作用矩陣乘法來代替，進而使用GEMM算法來間接進行卷積操作，這使得卷積操作可以在任何包含GEMM的平臺上進行，并且受益于矩陣乘法的高效性，任何針對GEMM的改進和研究都能有助于卷積運算效率的提升，從而提高模型的運算速度，因此目前大部分主流的神經網絡框架，例如Tensorflow、Pytorch和Caffe都使用基于GEMM的方法來在底層代碼中實現卷積。

具體的，基于GEMM的卷積方法需要借助于 im2col或im2row buffer來內存轉換，使得數據格式滿足GEMM算法的輸入要求，從而將卷積操作轉化為GEMM操作，然而這個轉換過程是一個計算開銷和內存開銷都比較大的過程，特別是在輸入channel數較小時，這個過程會在整個卷積過程中占有很大的比例。簡言之，就是在卷積過程中，每個pixel都會被多次重復的轉換，這是不必要的計算開銷。因此有許多工作都在對這一過程進行改進，本文工作提出了一種改進算法——間接卷積算法（Indirect Convolution algorithm），主要有以下兩個優(yōu)點：

1、去掉了im2row的轉換過程，這使得算法性能有了巨大的提升（up to 62%）。

2、用了一個更小的indirection buffer來代替原來的im2row buffer。不同于im2row buffer的大小隨著輸入channel數線性增加，indirection buffer沒有這個特性，因此indirection buffer的內存占用特性非常有利于輸入channel數較多時的卷積操作。

間接卷積算法

原始的GEMM通過如下計算來不斷迭代進行矩陣運算操作并輸出矩陣：

其中A是輸入張量，B是一個常量濾波器，C是輸出矩陣，在傳統(tǒng)的im2col+GEMM算法中，通常α=1而β=0，原始GEMM操作示意圖如下：

圖1 原始GEMM操作

其中 im2col buffer 代表矩陣A，filter tensor 代表矩陣B，A和B的乘積就是輸出copy表示將輸入的張量展開為一個二維矩陣，也就是im2col buffer。可以看到buffer的每一行則是由固定個數（步長）的pixel展開成一維的向量組成的，這些pixel都在原始tensor中的一個patch內，在經過和filter tensor相乘后，由于矩陣行列相乘得到一個元素，因此這幾個pixel的信息都被整合成了一個值，也就是對他們進行了卷積操作。最后在輸出矩陣C中，行數rows代表輸出的像素點個數，columns代表輸出的channel數。可以看到buffer的columns是和輸入channel數有關的。

為了降低buffer帶來的開銷，作者提出了一種間接矩陣乘法的思想，不把輸入的tensor直接展開并存儲在buffer中，而只是在buffer中存放每個pixel在input tensor的坐標，也就是從存數據變成了存地址（類似于指針pointer思想），這樣不管channel數有多少，存的地址信息始終只有二維，極大的降低了buffer的計算和存儲開銷，如下圖：

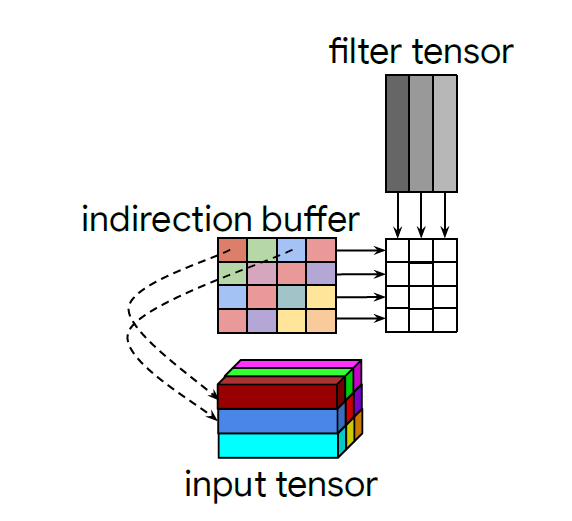
圖2 indirect convolution

當然，由于buffer中存的是地址信息，因此不能直接和filter做矩陣乘法，所以就只能通過在buffer的行間進行循環(huán)，根據該行的pointer找到對應的輸入數據，再將輸入數據與kernel相乘，并與之前循環(huán)的結果拼接起來，從而間接的實現矩陣乘法，因此叫做indirection buffer。

對于不同的卷積步長，只需要將不同步長對應的卷積patch位置確定即可。而對于padding策略，將指向填充位置的pointer對應的輸入pixel的向量值全部設置為0。

間接卷積算法的缺點

間接卷積算法作為GEMM-BASED CNN算法的一種改進，能極大的提升計算效率，但是存在以下幾個限制：

1. 這個算法是為NHWC layout設計的，也就是說應用范圍比較窄，不能和目前的主流方法相比。

2. 算法適用于前向傳播中的卷積操作，而在反向傳播中作用不大，不及基于col2im和row2im的算法。

3. 具有和GEMM相同的缺點，在深度小卷積核的卷積操作中效率并不好。

實驗測試結果

Efficient Deep Learning for Computer Vision主要聚焦于如何將深度學習部署到移動設備上，因此本文的工作主要在移動設備和移動芯片上進行測試，結果如下：

可以看到一旦步長增加，那么Indirect convolution帶來的性能提升就會明顯下降，這是因為步長越大，在原始的GEMM算法中重復計算的量就會減小，因此原始GEMM的性能本身就會提升，而indirect convolution并不受益于步長增加。