"做到無招勝有招,才能成為真正的高手",而在數(shù)學(xué)競賽于江湖成立的125年里,有這樣一群高手,他們以各種獨(dú)特,具有創(chuàng)造性的解法在數(shù)學(xué)江湖中留下赫赫威名,解法之逆天連眾多的數(shù)學(xué)宗師都為之驚嘆和折服。
1894年,位于歐洲中部的匈牙利數(shù)學(xué)物理協(xié)會通過了一個影響數(shù)學(xué)界近125年的決議,他們決定每年的10月在全國舉辦一項名為中學(xué)數(shù)學(xué)競賽的賽事,這個賽事為匈牙利造就了一大批與國土面積及人口數(shù)量極不成比例的數(shù)學(xué)大師,像被譽(yù)為匈牙利現(xiàn)代數(shù)學(xué)之父的費(fèi)葉,航天動力學(xué)的奠基人馮·卡曼,組合學(xué)家寇尼希,哈爾測度與哈爾積分的提出者哈爾,對泛函分析有著重大貢獻(xiàn)的黎茨,
在匈牙利數(shù)學(xué)競賽所造就的大師們登上世界舞臺之后,全世界無數(shù)國家都紛紛投去了驚奇和艷羨的目光,然后俄羅斯、保加利亞、波蘭、中國、印度、德國、英國、澳大利亞、美國等國家先后開始舉辦這一數(shù)學(xué)賽事,1934年,俄羅斯的前身蘇聯(lián)在列寧格勒大學(xué)舉辦了中學(xué)數(shù)學(xué)奧林匹克競賽,首次將數(shù)學(xué)考試與公元前776年的古希臘奧林匹克體育競賽聯(lián)系了起來,接著一項名為國際數(shù)學(xué)奧林匹克(簡稱IMO)的賽事緩緩地在數(shù)學(xué)江湖中拉開了宏偉的故事序幕,在2018年于羅馬尼亞舉辦第59屆比賽已經(jīng)有整整116個門派(國家)參與到其中,
金庸先生所著的《笑傲江湖》第十章中風(fēng)清揚(yáng)對令狐沖說過這樣一句話:"做到無招勝有招,才能成為真正的高手",而在數(shù)學(xué)競賽于江湖成立的125年里,有這樣一群高手,他們以各種獨(dú)特,具有創(chuàng)造性的解法在數(shù)學(xué)江湖中留下赫赫威名,解法之逆天連眾多的數(shù)學(xué)宗師都為之驚嘆和折服.
國際數(shù)學(xué)奧林匹克至今已經(jīng)舉辦了整整59屆,
比賽在每年的7月份兩個上午舉行,每次4.5小時,各解答3道題,每道題7分,設(shè)有金銀銅獎,三個獎項的獲得者總?cè)藬?shù)不超過參賽人數(shù)的一半,比例一般為1:2:3,在59屆的歷史長河中,雖然少但每屆都有一些數(shù)學(xué)天賦十分驚艷的選手以滿分的成績坐上"武林盟主"的無上寶座,
但是這個無上寶座并不是選手最渴望的獎項,有一個十分特殊的獎項,它比滿分更難獲得,從2005年至今整整14年,無一人獲得此獎項,它名為特別獎,假如某個選手對某道試題所作的解答非常漂亮,有獨(dú)到之處,與事先擬定的標(biāo)準(zhǔn)解答更加簡潔的話,不論這名選手總分是多少,他就可以獲得特別獎,
如果說獲得滿分難如登天的話,那么獲得特別獎就是難如逆天,
在1977年于南斯拉夫舉辦的第19屆比賽里,來自英國的John Rickard選手不僅僅以40分最高分的成績獲得金牌,并且他對越南所提供的第二題以用兩個互素的正整數(shù)p和q來代替題中的7與11,得出了最大項數(shù)為p+q-2,因?yàn)檫@一精彩無比的解法,使得他當(dāng)之無愧獲得了那年的特別獎.

1983年,在法國舉辦的第24屆比賽里,
總計有32個國家,179名數(shù)學(xué)高手參與其中,但是這些高手都活在了一名叫Bernhard Leeb德國選手所制造的恐懼之中,他不僅以滿分的成績坐上了"武林盟主"的寶座,而且對美國所提供的第六題的"逆天"解法使得他還獲得了特別獎,
他僅僅使用了一個等式就解決了當(dāng)年比賽最難的第六題,他假定a是最大的邊,這時(2)式右邊的兩項都是非負(fù)的,因而(2)式左邊也是非負(fù)的,即(1)式成立,不僅如此,從(2)式還容易看出當(dāng)且僅當(dāng)a=b=c,即這三角形為正三角形時(1)中等號成立,
解法之簡單,讓被譽(yù)為解題大師的單墫教授在《數(shù)學(xué)競賽史話》一書中都為之驚嘆,而國內(nèi)也曾有一些雜志刊登過(1)的簡便證明,但很遺憾是錯誤的,而這也間接證明了獲得特別獎的有多么困難,
而滿分外加特別獎也讓他成為了那年當(dāng)之無愧的大魔王選手.

1986年,
在波蘭舉辦的第27屆國際數(shù)學(xué)奧林匹克上,我們首次派出了滿員的六人隊伍,來自天津南開中學(xué)的李平立、河南省實(shí)驗(yàn)中學(xué)的方為民、上海大同中學(xué)的張浩、西安八十五中學(xué)的荊秦、湖北黃岡中學(xué)的林強(qiáng)、還有來自江蘇泰縣姜堰中學(xué)的沈建,這一年我們的表現(xiàn)讓所有國家都為之震驚,因?yàn)樵谝荒曛拔覀兊目偡峙琶箶?shù)第六,而在這一年里我們?nèi)〉昧丝偡值谒牡钠孥E般成績,
但是這一亮眼的成績卻被來自美國的Joseph Keane選手搶了風(fēng)頭,他差點(diǎn)成功復(fù)制了三年前Bernhard Leeb選手的"逆天之路",他與滿分僅有一分之差,而他對那屆比賽中最難的第三題獨(dú)特解法也讓其獲得了全場唯一的特別獎,其無比驚艷的表現(xiàn)也蓋過我們以及三位滿分選手的風(fēng)頭.

在國際數(shù)學(xué)奧林匹克的歷史長河中,
負(fù)責(zé)命題的主試委員會從來沒有辦成這樣一件事:編出一道題目,使得每名選手都束手無策,但是相反,有這樣一道題目曾讓整整49個國家領(lǐng)隊組成的主試委員會一籌莫展,后來不得已,只能將題目送到四位頂尖的數(shù)論專家手上,但是這四名已然成為了數(shù)學(xué)家的絕世高手在花了一整天的時間仍無法解出,
1988年,于澳大利亞舉辦的第29屆比賽上,由德國所提供的第六道數(shù)論題成為了當(dāng)時歷屆比賽中得分率最低的一道題,難到什么程度?49個國家,268名來自各國的最頂尖參賽選手的平均分僅僅只有0.6分,當(dāng)年剛滿12歲的數(shù)學(xué)天才陶哲軒也參加了比賽,但同樣也敗在了這道題的手上,
全場僅有12個人答對,來自四川彭縣中學(xué)的何宏宇和上海復(fù)旦附中的陳晞在此名單中,而來自保加利亞的Emanouil Atanassov選手不僅僅解出了這道題,并且解法之簡單堪稱逆天!

1989年,
在德國舉辦的第30屆比賽上,我們距離第一次參賽僅僅只過去了四年,但是已經(jīng)沒有任何一個國家敢小瞧我們這支年輕的隊伍,由馬希文和單墫教授組成的領(lǐng)隊,和來自重慶永川中學(xué)的羅華章、新疆石河子五中的蔣步星、東北師范大學(xué)附中的俞揚(yáng)、江西景德鎮(zhèn)景光中學(xué)的霍曉明、四川成都九中的唐若曦、人大附中的顏華菲為中國拿下了首個團(tuán)隊總分第一,
而來自新疆石河子五中的蔣步星對第六道題所給出的不必計算“對應(yīng)”的精彩解法,雖然沒能獲得特別獎,但是也讓在場所有人為之喝彩.

2005年,
那一年被人稱為"數(shù)學(xué)競賽中的奇跡年",在墨西哥舉辦的第46屆國際數(shù)學(xué)奧林匹克上,有一個無比精彩的解法橫空出世,據(jù)說當(dāng)時在場的人在看到這一解法時,無一例外的都被震驚的說不出話來,有人曾這樣評價它:"數(shù)學(xué)競賽有史以來最精彩的解法",
那一年由韓國所提供的第三題,因?yàn)殡y度極高,讓來自91個國家、513名選手的平均分僅僅只有0.91分,但還是有16名選手以滿分的成績傲視群雄,其中包括來自天津耀華中學(xué)的任慶春、上海華東師大二附中的刁晗生、江西師范大學(xué)附中的羅曄、上海復(fù)旦附中的邵烜程,
但是所有選手的亮眼表現(xiàn)都被來自一個人口僅有355萬,過去五年團(tuán)隊總分平均排名僅僅為第32名的摩爾多瓦無情鎮(zhèn)壓,來自這一國家的Iurie Boreico選手僅僅只用了兩行就解決了最難的第三道題,因?yàn)楹唵蔚揭凰浚┝Φ剿烈鈾M行,因此他在間隔十年之后,獲得了主試委員會再次頒出的特別獎,
不僅如此,他還是16名滿分選手的其中之一,
比起1983年來自德國Bernhard Leeb選手的滿分加特別獎的逆天之路,他的戰(zhàn)績顯得更加可怕,因?yàn)樵?006年,他再次參賽并且再一次獲得了滿分,而他也成為了國際數(shù)學(xué)奧林匹克唯一一個兩屆滿分外加特別獎的選手.

除了國際數(shù)學(xué)奧林匹克這一賽場,
在國內(nèi)舉辦的數(shù)學(xué)競賽中,也曾經(jīng)出現(xiàn)過讓眾多數(shù)學(xué)宗師都為之贊嘆的解法,1985年,為了促使我國的中學(xué)生數(shù)學(xué)競賽活動更上一層樓,在那年中國數(shù)學(xué)會成立五十周年紀(jì)念活動期間,由中國數(shù)學(xué)會與南開大學(xué)、北京大學(xué)、復(fù)旦大學(xué)、中國科技大學(xué)四所大學(xué)的數(shù)學(xué)系協(xié)商,決定聯(lián)合舉辦全國中學(xué)生數(shù)學(xué)冬令營,冬令營的營員是來自全國各省市、自治區(qū)的中學(xué)生,他們是全國高中數(shù)學(xué)聯(lián)合競賽的優(yōu)勝者,在為期約一周的冬令營期間,除了數(shù)學(xué)講座,參觀游覽等活動外,最重要的事情就算分兩天舉行的數(shù)學(xué)競賽,和IMO相似,在每天4.5小時的時間里,參賽選手要解答三道難度極高的數(shù)學(xué)競賽題,
在1986年,第一屆冬令營于天津舉行,
在那屆比賽中有兩名選手的解法讓當(dāng)年的命題組成員張筑生、常庚哲、裘宗滬等人都為止驚嘆,來自上海中學(xué)女學(xué)生邱隆東對Langford問題特例的第五題所給出的奇偶分析新解法以及來自揚(yáng)州市姜堰中學(xué)沈建在只用到很少一點(diǎn)復(fù)數(shù)知識,干凈利落地把第三道題給解決掉,不僅如此,他還推廣了結(jié)果,證明了比原命題更強(qiáng)的結(jié)論.


1987年,
在北京舉辦的第二屆冬令營上,來自上海向明中學(xué)的選手潘子剛對有著伯恩多項式背景的第二題第二問所給出的構(gòu)造性證明,表現(xiàn)出對"對稱性"的敏銳直覺與深刻洞察讓他獲得了冬令營的第一個特別獎!

而在第三屆冬令營上,
來自湖北潛江縣向陽中學(xué)的羅小奎選手對第四道第二問極其簡潔漂亮的"靈感"解法讓他獲得了那屆比賽的特別獎,這一解法的精妙之處在于受n-1的啟示,把a(bǔ)12+a22+a32這三項之和轉(zhuǎn)化為兩項a12+a22+a32/2之和,從而把題設(shè)不等式左邊括號內(nèi)的n項變?yōu)閚-1項之和,這一精彩解法也讓李成章、張筑生等數(shù)學(xué)宗師組成的命題組拍手叫絕!

1980年,
在大連召開了第一屆全國數(shù)學(xué)普及工作會議,會議決定把全國數(shù)學(xué)競賽作為中國數(shù)學(xué)會及各省、市、自治區(qū)數(shù)學(xué)會的一項經(jīng)常性工作,并正式定名為"全國各省、市、自治區(qū)高中聯(lián)合數(shù)學(xué)競賽",并確定每年的10月份于中國數(shù)學(xué)會的支持下,由一個省作為東道主舉辦其比賽,
1990年,第十屆聯(lián)賽由吉林省作為東道主,那屆比賽有一道題目的標(biāo)準(zhǔn)答案曾使得一些閱卷教師都感到費(fèi)解,而來自陜西省西安市85中學(xué)的田魯在解答中卻整體而本質(zhì)地把握題意,先證第二問,后得第一問,整個解答過程十分淺顯和簡明,堪稱一絕!

同年,
來自華東師大二附中的樓捷同學(xué)對于二試的第3題的解法也妙不可言,遠(yuǎn)比標(biāo)準(zhǔn)答案簡明,漂亮,充分顯示了參賽選手所具有的迅速推理和轉(zhuǎn)變思考方向的數(shù)學(xué)能力.

在第21屆全蘇數(shù)學(xué)競賽上,
來自北京四中的袁峰同學(xué)以不可思議的聯(lián)想,用一簡潔、直觀的證法直接透過了代數(shù)現(xiàn)象抓住了幾何實(shí)質(zhì),而這一解法也曾讓羅增儒、朱華偉等在數(shù)學(xué)競賽領(lǐng)域的宗師人物都為之叫好.

1990年,
整個北京都在為了迎接9月份的亞運(yùn)會如火如荼地準(zhǔn)備著,并沒有多少人知道在這一年,亞洲第一次承辦的國際數(shù)學(xué)奧林匹克也將在這個城市拉開帷幕,整個中國數(shù)學(xué)界都在為這一賽事奔波著,無數(shù)名震江湖的數(shù)學(xué)宗師都參與其中,在那一年里,我們打破了以往參與訓(xùn)練和命題工作人員最多的記錄,
在那年的冬令營上,有一道題目是由來自上海教育出版社葉中豪先生所發(fā)現(xiàn)的一個箏形蝴蝶定理,在那年比賽中,很少有選手能解出此題,命題組利用圖形的對稱性用解析法給出了證明,但是計算量十分巨大,當(dāng)時,命題組成員的單墫、杜錫錄兩位教授都希望能有一個簡單的方法證明這個定理,
后來,當(dāng)時為中國科學(xué)院研究員的張景中先生利用三角知識給出了下方的證法1,又避開三角函數(shù)與正弦定理,利用面積關(guān)系給出了證法2,并由此引出了十個全新的命題.
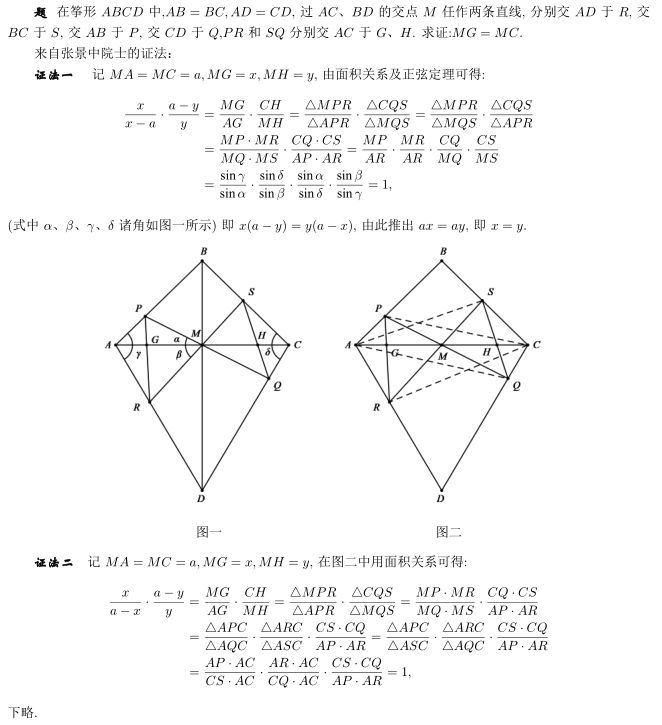
而在1990年的集訓(xùn)隊中,
當(dāng)時正讀初三,也是后來第35屆國際數(shù)學(xué)奧林匹克金牌得主的姚建綱選手對南斯拉夫給我們所提供的一道預(yù)選題給出了十分出人意料的證明,其漂亮程度讓當(dāng)時集訓(xùn)隊命題組的所有成員都為之叫好.

在1992年的集訓(xùn)隊訓(xùn)練期間,
有一名選手巧妙利用了垂心的性質(zhì),以十分簡潔的解法證明了下方的題目,而原命題者所給出的三角證法非常復(fù)雜,也由此可見,這一解法的精彩程度.
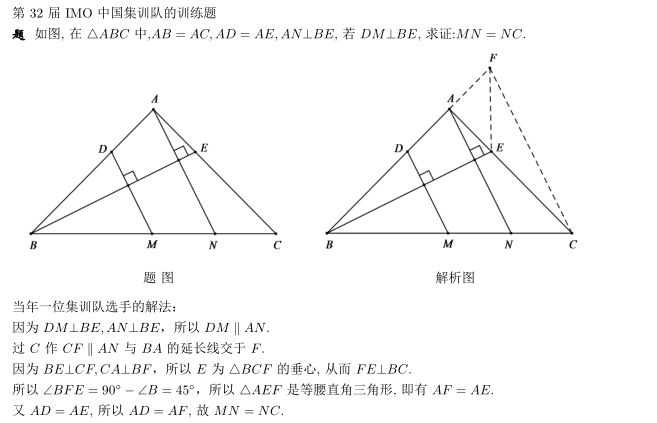
同年,
在俄羅斯舉辦的第33屆國際數(shù)學(xué)奧林匹克上,由意大利所提供第五題是那屆比賽中得分率最低的題目,那道題目的幾何直觀非常清楚,但是由原供題國所給出的證明思路卻不夠清晰,方法不夠自然,其證明幾乎完全脫離了幾何直觀,特別是引入了相當(dāng)抽象的集合T和映射f,結(jié)論好像是借助于抽象的手段變戲法變出來的,
而曾帶領(lǐng)中國拿下五次IMO團(tuán)隊總分第一的張筑生教授給出了一個十分漂亮的證明.

在1993年中國國家隊選拔賽上,
來自河南師大的夏興國教授曾提供了一道題目,在當(dāng)年參賽的二十余名數(shù)學(xué)高手中,僅有后來獲得了第34屆國際數(shù)學(xué)奧林匹克金牌的劉煬選手答對,他所采用的構(gòu)造方法雖然十分常見,但其技巧卻是十分高超和新穎的,
特別是論證k+1色圖時,對一些點(diǎn)的顏色的改變,其技巧更是耐人尋味.

在1980年,
于芬蘭、英國、匈牙利、瑞典舉辦的四國數(shù)學(xué)競賽上,也有一道題目所提供的解答十分繁瑣,前后整整用了四次歸納法,在譯成中文之后,將近有4000多字,當(dāng)時中國科技大學(xué)的白志東先生對此題采用一個十分大膽的處理方法,
加強(qiáng)命題,出奇制勝地給出了十分絕妙簡潔的證明!

在國際數(shù)學(xué)奧林匹克賽場上,
當(dāng)然也有原供題國提供的解答是十分精彩漂亮的,在保加利亞所舉辦的第17屆比賽上,由蘇聯(lián)所提供的第五題的原解法就十分簡潔優(yōu)雅,其利用到了著名的九余法.

曾創(chuàng)造了中國數(shù)學(xué)奧林歷史上,
第一個在國家集訓(xùn)隊的所有考試中均獲得滿分的選手,在第49屆、50屆兩次國際數(shù)學(xué)奧林匹克上也均獲得滿分,并且在2013年又獲丘成桐大學(xué)生數(shù)學(xué)競賽個人全能金獎,并獲得了五個單項獎中的四個金獎,一個銀獎,被數(shù)學(xué)江湖人稱"教主"的韋東奕在2008于上海的國家隊培訓(xùn)期間,對上海大學(xué)冷崗松教授從美國數(shù)學(xué)月刊找的一道訓(xùn)練題給出的證明也十分直白和精彩,
大多數(shù)選手所提供的都是圖論證法,而韋教主僅用了一下極端分析,就將這道題目給解出,解法自然而優(yōu)雅,直到今日,冷崗松教授還經(jīng)常會向競賽剛?cè)腴T的學(xué)生講解這一方法,并戲稱這是"韋方法".

曾是2006年中國數(shù)學(xué)國家隊隊員,
在第31屆國際數(shù)學(xué)奧林匹克獲得滿分,后來在北京大學(xué)畢業(yè)之后,去到龍泉寺出家的柳智宇其數(shù)學(xué)才華也曾給冷崗松教授留下了深刻的印象,他和人討論幾何題從不畫圖也不看圖,但是口中卻能準(zhǔn)確無誤說出諸多點(diǎn)線位置,從不忘記和混亂,他的幾何和組合十分突出,因此造就了一個少見的組合幾何高手,在集訓(xùn)隊選拔時幾個組合幾何難題能解出者寥寥無幾,而他所提供的解法卻令人拍案叫絕,在當(dāng)年的IMO上,第六道題便是一個組合幾何難題,全世界僅有3人做對,而他就是其中之一,并且協(xié)調(diào)組專家們都一致認(rèn)為他的解法比標(biāo)準(zhǔn)答案還要漂亮精彩,
在那年3月于沈陽東北育才中學(xué)舉行的第4次小考中,由林常教授所提供的一道題頗有難度,得滿分的選手不多,而柳智宇對于這一問題給出了一個十分精妙的解法,它不僅簡單,而且很好地揭示了問題的本質(zhì):對于a×b棋盤,其中g(shù)cd(a,b)=1,如果將對角線ab等分,則紅線段長度比藍(lán)線段長度恰好多一個等分單位.

同樣是兩屆IMO滿分,被許多人稱為"解題無敵"的羅煒,對于在杭州學(xué)軍中學(xué)舉辦的第33屆中國數(shù)學(xué)奧林匹克第五題的解法也是十分的有趣和精妙.


在羅增儒教授所著的《中學(xué)數(shù)學(xué)競賽的內(nèi)容與方法》中,他介紹了這樣一道題目,此題連小學(xué)生都能聽明白,但是其所體現(xiàn)的解題藝術(shù)卻是十分的高超,體現(xiàn)了一種無與倫比的美:大學(xué)的思想+小學(xué)的知識.

曾經(jīng)也是IMO滿分的汪建華曾談到他上小學(xué)時的一件事,
當(dāng)他剛掌握"韓信點(diǎn)兵"的時候,遇到這樣一道題:一個數(shù),除以3余2,除以5余4,除以7余6,此數(shù)最小為幾?開始的時候,他套用了口訣,很快地得到了答案,但后來他又想了想,并且想到了一個更好的解法,那就是將此數(shù)加上1之后,可被3、5、7整除,于是此數(shù)為3×5×7-1=104,而這個題的解法曾使得當(dāng)時上小學(xué)的他大受鼓舞,讓他開始遇到每一個數(shù)學(xué)問題時就投入到獨(dú)立思考的過程中,也大大增強(qiáng)了他學(xué)習(xí)數(shù)學(xué)的興趣,
而一道國際水平的競賽題,如果它的解法不能體現(xiàn)數(shù)學(xué)的美,缺乏簡潔、奇異與獨(dú)創(chuàng),那么是很難獲得主試委員會的認(rèn)可的,但需要強(qiáng)調(diào)的是,競賽的技巧并不是低層次一招一式或妙手偶得的雕蟲小技,
它既是使用數(shù)學(xué)技巧的技巧,又是創(chuàng)造了數(shù)學(xué)技巧的技巧,
更加準(zhǔn)確確切地說,這是一種數(shù)學(xué)創(chuàng)造力,一種思維層次,一種獨(dú)立于史詩、音樂、繪畫之外的數(shù)學(xué)美,而在數(shù)學(xué)奧林匹克江湖125年里,曾經(jīng)流傳著25個"逆天"解法的精彩故事,并讓無數(shù)人扣扣相傳,津津樂道.
-
數(shù)學(xué)
+關(guān)注
關(guān)注
0文章
99瀏覽量
19264 -
數(shù)學(xué)競賽
+關(guān)注
關(guān)注
0文章
2瀏覽量
3178
原文標(biāo)題:在數(shù)學(xué)奧林匹克的125年里,這25個逆天解法稱霸江湖!
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
特斯拉上海超級工廠五周年里程碑
阿里巴巴整合電商資源,成立全新電商事業(yè)群
Kimi發(fā)布新一代數(shù)學(xué)推理模型k0-math
傅里葉變換的數(shù)學(xué)原理
安徽農(nóng)信系統(tǒng)慶祝省聯(lián)社成立20周年勞動技能競賽,千視 P3 扮演了怎樣的角色?

2024年度OpenHarmony競賽訓(xùn)練營頒獎——創(chuàng)新驅(qū)動,培育未來科技人才
大學(xué)生電子設(shè)計競賽全面擁抱AI,2024年度“瑞薩杯”有些不一樣

LED顯示屏江湖:SMD、COB、MIP、GOB,誰是下一個C位?

2020-2022-2024年TI杯全國大學(xué)生電子設(shè)計競賽官方推薦芯片對比分析比較
當(dāng)AI與數(shù)學(xué)同時走下神壇





 數(shù)學(xué)競賽于江湖成立的125年里,有這樣一群高手
數(shù)學(xué)競賽于江湖成立的125年里,有這樣一群高手











評論