設計控制系統時應滿足多種性能指標,但首要的技術要求是系統全部時間內必須穩定。一般來說,穩定性成為區分系統是否有用的標志。從實際應用的角度來看,可以認為只有穩定系統才有用。
3.1.1 穩定性的基本概念
原來處于平衡狀態的系統,在受到擾動作用后都會偏離原來的平衡狀態。所謂穩定性,就是指系統在擾動作用消失后,經過一段過渡過程后能否回復到原來的平衡狀態或足夠準確地回復到原來的平衡狀態的性能。若系統能恢復到原來的平衡狀態,則稱系統是穩定的;若干擾消失后系統不能恢復到原來的平衡狀態,偏差越來越大,則系統是不穩定的。
系統的穩定性又分兩種情況:一是大范圍內穩定,即起始偏差可以很大,系統仍穩定。另一種是小范圍內穩定,即起始偏差必須在一定限度內系統才穩定,超出了這個限定值則不穩定。對于線性系統,如果在小范圍內是穩定的,則它一定也是在大范圍內穩定的。而對非線性系統,在小范圍內穩定,在大范圍內就不一定是穩定的。本章所研究的穩定性問題,是線性系統的穩定性,因而是大范圍內的穩定性問題。
一般來說,系統的穩定性表現為其時域響應的收斂性,如果系統的零輸入響應和零狀態響應都是收斂的,則此系統就被認為是總體穩定的。不難證明,對于線性定常系統,零輸入響應穩定性和零狀態響應穩定性的條件是一致的。所以線性定常系統的穩定性是通過系統響應的穩定性來表達的。
3.1.2 線性系統的穩定性
線性系統的特性或狀態是由線性微分方程來描述的,而微分方程的解通常就是系統輸出量的時間表達式,它包含兩部分:穩態分量(又稱強制分量)和瞬態分量(又稱自由分量)。穩態分量對應微分方程的特解,與外作用形式有關;瞬態分量對應微分方程的通解,是系統齊次方程的解,它與系統本身的參數、結構和初始條件有關,而與外作用形式無關。研究系統的穩定性,就是研究系統輸出量中的瞬態分量的運動形式。這種運動形式完全取決于系統的特征方程式,即齊次微分方程式,因為它正是研究擾動消除后輸出量運動形式的。
單輸入單輸出線性系統的傳遞函數一般表示為:
系統的特征方程式為
顯然,它是由系統本身的參數和結構所決定的。
3.1.3 線性系統穩定的充分必要條件
從上節的例子可以看出,線性系統穩定與否完全取決于其微分方程的特征方程根。如果特征方程的全部根都是負實數或實部為負的復數,則系統是穩定的。如果特征方程的各根中即使只有一個根是正實數或只有一對根是實部為正的復數,則微分方程的解中就會出現發散項。
由此可得出如下結論:線性系統穩定的充分必要條件是它的特征方程式的所有根均為負數或具有負的實數部分;或者說,特征方程式的所有根均在復數平面的左半部分。由于系統特征方程式的根就是系統的極點,所以又可以說,系統穩定的充分必要條件是系統的極點均在S平面的左半部分。
3.1.4 勞斯-赫爾維茨(Routh-Hurwitz)穩定判據
判別系統穩定性最基本的方法是根據特征方程式的根的性質來判定。但求解高于三階的特征方程式相當復雜和困難。所以在實際應用中提出了各種工程方法,它們無需求特征根,但都說明了特征根在復平面上的分布情況,從而判別系統的穩定性。本節主要介紹代數判據。
(一) 系統穩定性的初步判別
設已知控制系統的特征方程
式中所有系數均為實數,且a0>0
系統穩定的必要條件是上述特征方程式所有系數均為正數。可簡單證明如下:
將特征方程寫成用特征根表達的形式
 |
(3-1) |
假如所有特征根均在S平面的左半部,即-σi<0,-αk<0,則式(3-1)中的σi<0,αk<0 (i=1,…,q;k=1,…,l;q+2l=n),若把式(3-1)的乘積展開,s多項式的各項系數必然均大于零。
根據這一原則,在判別系統穩定性時,可事先檢查一下系統特征方程式的系數是否均為正數。如果有任何一項系數為負數或等于零(即缺項),則系統是不穩定或臨界穩定的。假如只是判別系統是否穩定,到此就不必作進一步的判別了。如果系數均為正數,對二階系統來說肯定是穩定的(必要且充分),但對二階以上的系統,還要作進一步的判別。
(二) 勞斯判據(Routh)
將系統的特征方程寫成如下標準形式
并將各系數組成如下排列的勞斯表:
| sn |
a0 |
a2 |
a4 |
a6 |
... |
| sn-1 |
a1 |
a3 |
a5 |
a7 |
... |
| sn-2 |
b1 |
b2 |
b3 |
b4 |
... |
| sn-3 |
c1 |
c2 |
c3 |
c4 |
... |
.
.
.
|
.
.
. |
.
.
. |
.
.
. |
.
.
. |
? |
| s2 |
e1 |
c2 |
? |
? |
? |
| s1 |
f1 |
e2 |
? |
? |
? |
| s0 |
g1 |
? |
? |
? |
? |
表中的有關系數為
………………………
系數bi的計算一直進行到其余的b值全部等于零為止。
………………………
這一計算過程一直進行到n行為止。為了簡化數值運算,可以用一個正整數去除或乘某一行的各項,這時并不改變穩定性的結論。
列出了勞斯表以后,可能出現以下幾種情況。
1.第一列所有系數均不為零的情況,這時,勞斯判據指出,系統極點實部為正實數根的數目等于勞斯表中第一列的系數符號改變的次數。系統極點全部在復平面的左半平面的充分必要條件是方程的各項系數全部為正值,并且勞斯表的第一列都具有正號。
例3-1 三階系統的特征方程為
D(s)=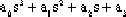 =0 =0
列出勞斯表
| s3 |
a0 |
a2 |
| s2 |
a1 |
a3 |
| s1 |
 |
? |
| s0 |
a3 |
? |
系統穩定的充分必要條件是
a0>0,a1>0,a2>0,a3>0,a1a2-a0a3>0
例3-2 四階系統特征方程為
D(s)= 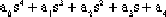 =0 =0
列出勞斯表
| s4 |
a0 |
a2 |
a4 |
| s3 |
a1 |
a3 |
0 |
| s2 |
 |
a4 |
? |
| s1 |
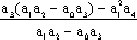 |
? |
? |
| s0 |
a4 |
? |
? |
四階系統穩定的充分必要條件是各項系數為正值,并且
a1a2-a0a3>0,a3(a1a2-a0a3)-a12a4>0
例3-3 設已知系統的特征方程為
D(s)= 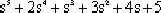 =0 =0
列出勞斯表
| s5 |
1 |
1 |
4 |
? |
| s4 |
2 |
3 |
5 |
? |
| s3 |
-1 |
3 |
0 |
(各元素乘以2) |
| s2 |
9 |
5 |
0 |
? |
| s1 |
32 |
? |
? |
(各元素乘以9) |
| s0 |
5 |
? |
? |
? |
由上表可以看出,第一列各數值的符號改變了兩次,由+2變成-1,又由-1改變成+9,因此該系統有兩個正實部的極點,系統是不穩定的。
2.某行第一列的系數等于零,而其余項中某些項不等于零的情況。在計算勞斯表中各元素的數值時,如果某行的第一列的數值等于零,而其余的項中某些項不等于零,那么可以用一有限小的數值ε來代替為零的那一項,然后按照通常方法計算陣列中其余各項。如果零(ε)上面的系數符號與零(ε)下面的系數符號相反,表明這里有一個符號變化。
例3-4 下列特征方程 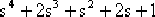 =0 =0
勞斯表
| s4 |
1 |
1 |
1 |
| s3 |
2 |
2 |
0 |
| s2 |
ε(≈0) |
1 |
? |
| s1 |
2-2/ε |
1 |
? |
| s0 |
1 |
? |
? |
現在考察第一列中各項數值。當ε趨近于零時,2-2/ε 的值是一很大的負值,因此可以認為第一列中的各項數值的符號改變了兩次。按勞斯判據,該系統有兩個極點具有正實部,系統是不穩定的。
3.某行所有各項系數均為零的情況,如果勞斯表中某一行的各項均為零,或只有等于零的一項,這表示在s平面內存在一些大小相等符號相反的實極點和(或)一些共軛虛數極點。為了寫出下面各行,將不為零的最后一行的各項組成一個方程,這個方程叫作輔助方程,式中s均為偶次。由該方程對s求導數,用求導得到的各項系數來代替為零的各項,然后繼續按照勞斯表的列寫方法,寫出以下的各行。至于這些根,可以通過解輔助方程得到。但是當一行中的第一列的系數為零,而且沒有其它項時,可以像情況2所述那樣,用ε代替為零的一項,然后按通常方法計算陣列中其余各項。
例3-5 已知系統的特征方程為
D(s)=  =0 =0
勞斯表中的s6~s3各項為
| s6 |
1 |
8 |
20 |
16 |
? |
| s5 |
2 |
12 |
16 |
0 |
? |
| s4 |
1 |
6 |
8 |
? |
(各元素乘以1/2) |
| s3 |
0 |
0 |
0 |
? |
? |
由上表看出,s3行的各項全為零。為了求出s3~ s0各項,將s4行的各項組成輔助方程:
A(s)= 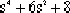
將輔助方程A(s)對s求導數,得 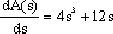
用上式中的各項系數作為s3行的各項系數,并計算以下各行的各項系數,得勞斯表為
s6
| s6 |
1 |
8 |
20 |
16 |
| s5 |
2 |
12 |
16 |
0 |
| s4 |
1 |
6 |
8 |
? |
| s3 |
0 |
12 |
? |
? |
| s2 |
3 |
8 |
? |
? |
| s1 |
3/4 |
? |
? |
? |
| s0 |
8 |
? |
? |
? |
從上表的第一列可以看出,各項符號沒有改變,因此可以確定在右半平面沒有極點。另外,由于s3行的各項皆為零,這表示有共軛虛數極點。這些極點可由輔助方程求出。
本例中的輔助方程是 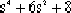 =0 =0
由此求得大小相等符號相反的虛數極點為 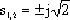 , ,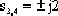
(三) 赫爾維茨判據(Hurwitz)
分析6階以下系統的穩定性時,還可以應用赫爾維茨判據。將系統的特征方程寫成如下標準形式
現以它的各項系數寫出如下之行列式:
行列式中,對角線上各元為特征方程中自第二項開始的各項系數。每行以對角線上各元為準,寫對角線左方各元時,系數a的腳標遞增;寫對角線右方各元時,系數a的腳標遞減。當寫到在特征方程中不存在系數時,則以零來代替。
赫爾維茨判據描述如下:系統穩定的充分必要條件在a0>0的情況下是,上述各行列式的各階主子或均大于零,即對穩定系統來說要求
赫爾維茨穩定判據雖然在形式上與勞斯判據不同,但實際結論是相同的。
例3-6 三階系統的特征方程為D(s)= 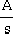 =0 =0
列出系數行列式 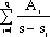
赫爾維茨穩定判據指出,該三階系統穩定的充分和必要條件是:
△1=a1>0
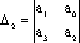 =a1a2-a0a3>0 =a1a2-a0a3>0
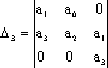 =a3(a1a2-a0a3)>0 =a3(a1a2-a0a3)>0
或者寫成系統穩定的充分必要條件是:
a0>0,a1>0,a2>0,a3>0,a1a2-a0a3>0
又如四階系統特征方程為
D(s)= 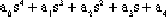 =0 =0
系統穩定的充分必要條件是:
a1>0
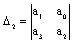 =a1a2-a0a3>0 =a1a2-a0a3>0
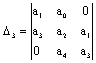 =a3(a1a2-a0a3)- a4>0 =a3(a1a2-a0a3)- a4>0
 =a4[a3(a1a2-a0a3)- =a4[a3(a1a2-a0a3)- a4]>0 a4]>0
或者寫成四階系統穩定的充分必要條件是:
a0>0,a1>0,a2>0,a3>0,a1a2-a0a3>0,
a1a2-a0a3>0,a3(a1a2-a0a3)- a4>0
以上得出的結果與前述勞斯判據所得的三階和四階系統穩定的充分必要條件完全一樣。
應用代數判據不僅可以判定系統是否穩定,還可以用來分析系統參數變化對系統穩定性的影響,從而給出使系統穩定的參數范圍。
例3-7 設反饋控制系統如圖3-1所示,求滿足穩定要求時K的臨界值。
解 系統閉環傳遞函數是 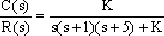
其特征方程為
D(s)=s(s+1)(s+5)+K=0
或  =0 =0
列出勞斯表
| s3 |
1 |
5 |
| s2 |
6 |
K |
| s1 |
 |
? |
| s0 |
K |
? |
按勞斯判據,要使系統穩定,其第一列應為正數,即
K>0,30-K>0
則有 0
從而得出滿足穩定的臨界值Kc=30。
例3-8 已知系統的閉環傳遞函數為 
求臨界放大系數Kc及其與參量T1、T2及T3的關系。
解 系統的特征方程為
D(s)=T1T2T3s3+(T1T2+T1T3+T2T3)s2+(T1+T2+T3)s+1+K=0
根據勞斯判據,穩定的充分必要條件是:特征方程的各項系數均大于零,并且a1a2-a0a3>0。現在系統的時間常數及放大系數均為正,所以滿足各項系數均大于零的條件。將各項系數代入a1a2-a0a3>0中,得
(T1+T2+T3)(T1T2+T1T3+T2T3)-T1T2T3(1+K)>0
或 1+K<(T1+T2+T3)(  + +  + +  ) )
從而得臨界放大系數
Kc=(T1+T2+T3)( + +  + +  )-1 )-1
由此式看出,T1、T2、T3中只要有一個足夠小,那么Kc就可以增大。決定Kc大小的,實際上并不是各時間常數的絕對值,而是其相對值,即取決于各時間常數的比值。將上式變換成
Kc=2+ 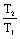 + + + + 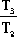 + + 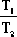 + + 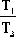 + + 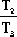
還可以求出開環增益臨界值Kc的極小值Kcmin與參量T1、T2及T3的關系。為此,先求出Kc對T1、T2及T3的偏導并令其為零。
= + +  - - - - 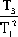 =0 =0
 = =  + +  - - 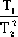 - -  =0 =0
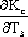 = =  + +  - - - - 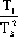 =0 =0
整理以上各式,即得
(T2+T3)( -T2T3)=0 -T2T3)=0
(T1+T3)( -T1T3)=0 -T1T3)=0
(T1+T2)(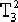 -T1T2)=0 -T1T2)=0
由此可見,T1、T2及T3必須同時滿足以上三式,Kc才有極值。又因為以上三式的形式是一樣的,所以能夠看出,只有
T1=T2=T3=T
時,Kc才有極值。為進一步確定極值是極大值抑或極小值,可從Kc對T的二階偏導來判斷。由于
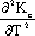 = =  >0 >0
故知極值為極小而非極大。
將T1=T2=T3=T的關系代入到Kc中,則有
Kcmin=8
這個結論表明,由三個非周期環節串聯組成的反饋控制系統,當三個非周期環節的時間相等時,系統的臨界開環增益最低。
若取T1=10T2,T2=T3,則可求得Kc=24.2。時間常數的數值錯開得愈多,則Kc可以提高得愈多。 |  電子發燒友App
電子發燒友App

 硬聲App
硬聲App

 347
347 931
931
 229
229
 1128
1128
 2025
2025
 3021
3021
 4
4 10
10 0
0 947
947 2
2 31
31 3
3 1
1 24
24 11811
11811 25
25 11138
11138
 28
28 1617
1617 3
3 242390
242390 6
6 23
23 67
67 21
21 28
28 24
24 28
28 4958
4958
 1561
1561 18
18 7
7 12
12 12
12 24
24 17
17 12
12 1423
1423
 24
24 37
37 21
21 44
44 513
513 21
21 618
618 7
7 134
134 115
115
評論