|
6.3.1 超前校正
用頻率法對系統進行超前校正的基本原理是:通過所加的校正裝置的相位超前特性來增大系統的相位裕量,改變系統開環頻率特性,并要求校正網絡最大的相位超前角
φm出現在系統新的剪切頻率處,使校正后系統具有如下特點:低頻段的增益滿足穩態精度的要求;中頻段對數幅頻特性的斜率為-20db/dec ,并具有較寬的頻帶,使系統具有滿意的動態性能;高頻段要求幅值迅速衰減,以減少噪聲的影響。
用頻率法對系統進行串聯超前校正的一般步驟可分為:
1)根據穩態誤差的要求,確定系統的開環增益K,并據此畫出未校正系統的伯德圖,并測出其相位裕量γ1。
2)由期望的相位裕量值γ ,計算超前校正裝置應提供的相位超前量 φ,即
式中的ε是用于補償因超前校正裝置的引入,使系統的剪切頻率增大而導致未校正系統相角遲后量的增加。ε值可以這樣估計的:如果未校正系統的開環對數幅頻特性在剪切頻率處的斜率為-40db/dec ,一般取ε=5°-10° ;如果該頻段的斜率為
-60db/dec ,則取ε=15°-20°。
3)根據所確定的最大相位超前角φm ,按式(6—8)算出相應的 α值,即
4)計算校正裝置在ωm處的幅值10lg1/α (參見圖6—5)。由未校正系統的對數幅頻特性圖,求得其幅值為-10lg1/α 處的頻率,則該頻率ωm就是校正后系統的開環剪切頻率ωm,即ωc=ωm 。
5)確定校正網絡的轉折頻率ω1 和ω2
| ? |
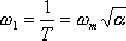 |
, |
6)畫出校正后系統的伯德圖,并驗算相位裕量是否滿足要求?如果不滿足,則需增大ε值,從步驟3)開始重新進行計算,直到滿足要求。
例 6—1 設一單位反饋系統的開環傳遞函數為: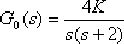
設計一超前校正裝置,使校正后系統的靜態速度誤差系數  等于 等于  ,相位裕量γ不小于 ,相位裕量γ不小于 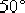 ,增益裕量 ,增益裕量 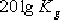 不小于 不小于 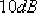 . .
解:(1)根據對靜態速度誤差系數的要求,確定系統的開環增益K。
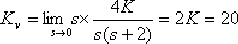 , , 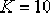
當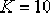 時,未校正系統的開環頻率特性為 時,未校正系統的開環頻率特性為

繪制未校正系統的伯德圖,如圖6—6中的虛線所示。由該圖或用Matlab中的margin命令,可得未校正系統的幅值裕量為無窮大,相位裕量約為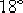 。 。
(2)根據相位裕量的要求確定超前校正網絡的相位超前角:
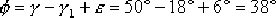
(3)由式(6—8)求得: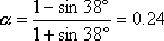
(4)超前校正裝置在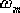 處的幅值為: 處的幅值為: 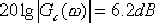
 ,在未校正系統的開環對數幅值對應的頻率 ,這一頻率即為校正后系統的剪切頻率 ,在未校正系統的開環對數幅值對應的頻率 ,這一頻率即為校正后系統的剪切頻率 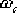 。 。
(5)確定超前校正網絡的轉折頻率 ,并確定超前裝置的傳遞函數。 ,并確定超前裝置的傳遞函數。
由 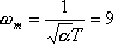 ,則 ,則 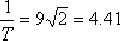 , ,  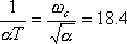
,于是求得超前校正網絡的傳遞函數為
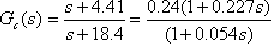
為補償因超前校正網絡的引入而造成系統開環增益的衰減,必須使附加放大器的放大倍數為 .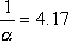
(6)校正后系統的開環傳遞函數為:

對應的伯德圖如圖6—15中的細實線所示。由該圖可見,校正后系統的相位裕量γ為 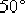 ,增益裕量為 ,增益裕量為 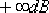 ,,滿足設計的要求。 ,,滿足設計的要求。
通過上例可以看出,串聯超前校正有如下特點;
1)這種校正主要對未校正系統中頻段的頻率特性進行校正,使校正后中頻段幅值的斜率為-20db/dec,且有足夠大的相位裕量。
2)超前校正會使系統瞬態響應的速度變快。由例6—1可知,校正后系統的剪切頻率由未校正前的6.3增大到9。這表示校正后系統的頻帶變寬,瞬態響應的速度變快;但系統抗高頻噪聲的能力也變差。
3)雖然超前校正一般能較有效地改善系統的動態性能,但當未校正系統的相頻特性曲線在剪切頻率ωc附近急劇地下降時,若用單級的超前校正網絡去校正,收效不大。因為校正后系統的剪切頻率向高頻段移動。在新的剪切頻率處,由于未校正系統的相角遲后量過大,因而用單級的超前校正網絡難于獲得較大的相位裕量。此時可采用多級串聯校正。
6.3.2 遲后校正
根據遲后校正網絡具有低通濾波器的特性,因而當它與系統的不可變部分Gc(s)串聯時,它對頻率特性的低頻段影響甚微,但會使系統開環頻率特性的中頻和高頻段增益降低,剪切頻率ωc減小,從而有可能使系統獲得足夠大的相位裕量。由此可見,遲后校正在一定的條件下,也能使系統同時滿足動態和靜態性能的要求。
不難看出,遲后校正的不足之處是:校正后系統的剪切頻率ωc會減小,頻帶變窄,瞬態響應速度變慢;同時,在剪切頻率ωc處,遲后校正網絡會產生一定的相角遲后量。為此,應盡可能地減少遲后角。理論上可選取 的兩個轉折頻率ω1 、ω2比
ωc越小越好,但考慮到物理實現上的可行性,一般取ω2=1/T=ωc/5 ~ωc/10為宜。
根據上述分析,用頻率法對系統進行遲后校正的一般步驟為:
1)根據給定靜態誤差系數的要求,計算系統的開環增益K。并畫出未校正系統的伯德圖,求出相應的相位裕量和增益裕量。
2)在已作出的相頻曲線上尋找一個頻率點,要求在該點處的開環頻率特性的相角為:φ=-180°+γ+ε
以這一頻率作為校正后系統的剪切頻率ωc 。上式中,γ為系統所要求的相位裕量,ε是補償因遲后網絡的引入而在剪切頻率ωc處產生的相位遲后量,工程上可取
ε=5°-10°。
3)設未校正系統在處ωc的幅值等于20lgβ,據此確定遲后網絡的β值。據此可保證在剪切頻率ωc處,校正后開環系統的幅值為0。
4)選擇遲后校正網絡中的一個轉折頻率ω2=1/T=ωc/5 ~ωc/10,則另一個轉折頻率為ω1=1/βT 。
5)畫出校正后系統的伯德圖,并求出校正后系統的相位裕量。校核設計指標,如果不滿足要求,則可通過改變T值,重新設計遲后校正網絡。
例6—2 設一單位反饋系統的開環傳遞函數為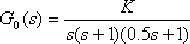
要求設計一串聯遲后校正裝置,使系統具有下列的性能指標:靜態速度誤差系數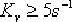 ;相位裕量γ不低于 ;相位裕量γ不低于 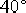 ;增益裕量不小于10dB。 ;增益裕量不小于10dB。
解:(1)調整開環增益K,使之滿足靜態速度誤差系數的要求。
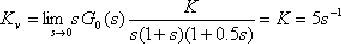
增益調整后系統的開環頻率特性為:
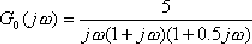
相應的伯德圖如圖6—16中的虛線所示。由該圖可知,未校正系統的相位裕量約等于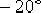 ,或使用Matlab中的margin函數,可得到校正前的系統是不穩定的。 ,或使用Matlab中的margin函數,可得到校正前的系統是不穩定的。
(2)在作出的相頻特性曲線上,根據下式確定相角
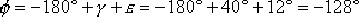
對應于這個φ角的頻率 ,并選它作為校正后系統的剪切頻率 ,并選它作為校正后系統的剪切頻率 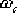 。 。
(3)計算  。由于未校正系統在 。由于未校正系統在  處的幅值等于20dB,即 處的幅值等于20dB,即 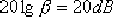 ,故β=10。 ,故β=10。
(4)取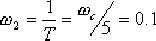 ,則 ,則 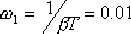 。這樣,遲后校正網絡的傳遞函數為: 。這樣,遲后校正網絡的傳遞函數為: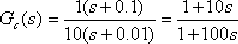
(5)校正后系統的開環傳遞函數為
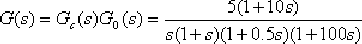
對應的伯德圖如圖6—16中的實線所示。由圖或由Matlab中的margin函數可知,校正后系統的相位裕量約為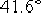 ,增益裕量約等于14dB,滿足設計要求。 ,增益裕量約等于14dB,滿足設計要求。
6.3.3 遲后-超前校正
如果未校正系統為不穩定,或對校正后系統的動態和靜態性能均有較高的要求時,只采用上述的超前校正或遲后校正,難于達到預期的校正效果。此時,宜對系統采用串聯遲后—超前校正。
應用頻率法設計遲后-超前校正裝置,即利用校正裝置的超前部分來增大系統的相位裕量,以改善其動態性能,但因加大了帶寬,易受高頻噪聲的影響,降低了系統的抗干擾能力;利用它的遲后部分來改善系統的靜態性能,但會惡化系統的動態性能,對系統的相對穩定性不利。因此采用這種校正方式,應合理應用遲后和超前校正各自的優點,克服它們各自的弱點,經多次試探才能成功。
例6—3 設一單位反饋系統的開環傳遞函數為:
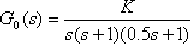
要求校正后系統具有下列的性能指標:相位裕量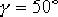 ;增益裕量 ;增益裕量 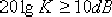 ;靜態速度誤差系數 ;靜態速度誤差系數 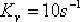 。。試設計一遲后—超前校正裝置。 。。試設計一遲后—超前校正裝置。
解:與超前校正和遲后校正相似,遲后—超前校正可按如下步驟進行:
(1)求取開環增益并作出伯德圖。其根據對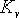 的要求,系統的增益K由 的要求,系統的增益K由
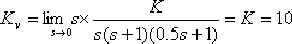
求得K=10。
未校正系統的伯德圖如圖6—17中的虛線所示。由圖可得到系統相位裕量等于 ,表明原系統是不穩定的。在這種情況下,如果采用超前校正,由于系統的剪切頻率的增大使原系統產生的遲后相位的增加比超前校正裝置提供的相位增加還快,這樣無法起到校正的作用,同時將增大剪切頻率,不利抑制噪聲。
(2)確定校正后系統的剪切頻率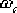 。在未對系統的快速性提出要求時,可選擇相頻特性上相角等于 。在未對系統的快速性提出要求時,可選擇相頻特性上相角等于 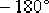 的頻率作為校正后系統的剪切頻率 的頻率作為校正后系統的剪切頻率 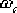 。在本題中,由未校正系統的相頻曲線可見,當 。在本題中,由未校正系統的相頻曲線可見,當 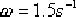 時, 時, 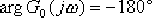 。選擇該頻率值作為校正后系統的剪切頻率 。選擇該頻率值作為校正后系統的剪切頻率 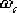 ,顯然較為合理。因為遲后—超前校正網絡在該頻率處產生 ,顯然較為合理。因為遲后—超前校正網絡在該頻率處產生 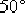 的相位超前角是完全能實現的,并且 的相位超前角是完全能實現的,并且 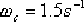 也不算小,使校正后的系統仍具有一定的響應速度。 也不算小,使校正后的系統仍具有一定的響應速度。
(3)確定遲后—超前網絡的轉折頻率。首先確定遲后部分的轉折頻率,令它的一個轉折頻率 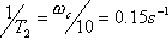 ,選取β=10,則另一個轉折頻率 ,選取β=10,則另一個轉折頻率 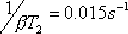 ,于是求得校正裝置遲后部分的傳遞函數為 ,于是求得校正裝置遲后部分的傳遞函數為
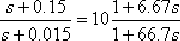
它在剪切頻率 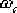 處產生約 處產生約 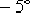 的相位遲后。接著確定超前部分的轉折頻率:由圖6—29可見,未校正系統在 的相位遲后。接著確定超前部分的轉折頻率:由圖6—29可見,未校正系統在  處的幅值為13dB,欲使該頻率成為校正后系統的剪切頻率,必須使該頻率點的開環幅值為0dB,即要求遲后—超前網絡在 處的幅值為13dB,欲使該頻率成為校正后系統的剪切頻率,必須使該頻率點的開環幅值為0dB,即要求遲后—超前網絡在 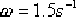 處產生-13dB的幅值。據此,通過點 處產生-13dB的幅值。據此,通過點 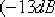 , 作一條斜率為 , 作一條斜率為 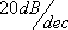 的直線,該直線與0dB線與-20dB的水平線的交點,它們分別為 的直線,該直線與0dB線與-20dB的水平線的交點,它們分別為  , , 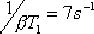 ,就是要求的超前部分的轉折頻率。因此超 ,就是要求的超前部分的轉折頻率。因此超
前部分的傳遞函數為: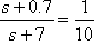 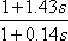
將校正網絡的遲后部分和超前部分的傳遞函數組合在一起,就得到遲后—超前校正網絡的傳遞函數:

(4)校正后系統的開環傳遞函數為:
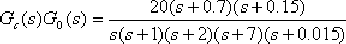
相應的伯德圖如圖6—17中的實線所示。校正后系統的相位裕量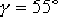 ,增益裕量13.6db,靜態速度誤差系數 ,增益裕量13.6db,靜態速度誤差系數 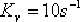 ,所要求的性能指標均已滿足。 ,所要求的性能指標均已滿足。
前面我們介紹了基于頻率法的串聯控制器的順向設計方法,即依據指標或設計要求,首先選擇三類控制器中的一種方式,然后按設計規則進行設計。事實上,若能根據指標設計出校正后的期望頻率特性,則根據:G(jω)=Gc(jω)G0(jω) ,由校正前后的幅頻特性和相頻,亦可得到待定的控制器。此法對于最小相位系統尤其有效。
6.3.4基于頻率法的Matlab串聯校正設計
根據上面對三類控制器頻率法設計思路的介紹,可總結出一般性的設計步驟:
(1)根據靜態性能指標,設計開環系統的增益,然后求出校正前系統的幅值裕量和相位裕量,并與設計要求比較;
(2)確定校正后期望的剪切頻率ωc,具體值的選取與選擇的校正方式(相位超前、遲后或遲后-超前等)相適應;
(3)根據待設計的校正裝置的形式和轉折頻率,計算有關參數,進而確定校正裝置;
(4)得出校正后系統,并校驗是否滿足設計要求。不滿足,則從(2)重新開始。
但畢竟,控制系統的設計是一項十分麻煩的工作,并需要大量的經驗,為此,可借助飛速發展的計算機仿真技術,簡化控制系統的設計工作。
本節介紹頻率法的MATLAB設計方法,主要利用伯德(Bode)圖進行系統的設計,常用的函數有:
Bode--—伯德圖作圖命令;
Margin—求取系統的幅值裕度和相位裕度;
Bode_asymp—伯德圖幅頻特性的漸近線(自編函數);
Semilogx—半對數作圖函數;
Logspace—用于在某個區域中產生若干頻點;
Nicols、Mgrid—用于Nicols曲線和等M圓、等N圓的作圖命令;
Nyquist—Nyquist曲線作圖命令;
Phase、Abs—求取復數行矢量的相角和幅值函數。 這些函數或命令大部分在第五章或第九章作過說明。
結合例6-4介紹采用Matlab進行設計的具體步驟,設計一個補償器
例6-4 對一給定的對象環節:
設計一個補償器,使校正后系統的靜態速度誤差系數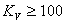 ,剪切頻率大于60,相位裕量 ,剪切頻率大于60,相位裕量 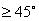 。 。
解:(1)首先根據對靜態速度誤差系數的要求,確定系統的開環增益K=100。
(2)寫出系統傳遞函數G0并計算其幅值裕量和相位裕量:
G0=tf(100,conv([1,0],[0.04,1]));
[Gm,Pm,Wcg,Wcp]=margin(G0);[Gm,Pm,Wcg,Wcp]
ans =
Inf 28.0202 NaN 46.9782
w=logspace(-1,3);[m,p]=bode(G0,w);
subplot(211),semilogx(w,20*log10(m(:)))
subplot(212),semilogx(w,p(:))
可以看到,未校正環節的幅值裕量無窮大,相位裕量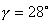 ,剪切頻率 ,剪切頻率 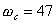 ,不滿足要求。其伯德圖如圖6-18a中的虛線所示。 ,不滿足要求。其伯德圖如圖6-18a中的虛線所示。
(3) 根據系統對動態性能的要求,可試探性引入一個超前補償器來增加相角裕量,則可假設校正裝置的傳遞函數為:
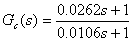
則可通過下列的Matlab語句得到校正后系統的幅值裕量和相位裕量:
Gc=tf([0.0262,1],[0.0106,1]);bode(Gc,w)
G_o=Gc*G0;[Gm,Pm,Wcg,Wcp]=margin(G_o);[Gm,Pm,Wcg,Wcp]
ans =
Inf 47.5917 NaN 60.3252
從而可得到補償器的Bode圖如圖6-18b所示。可以看出,在頻率 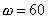 處系統的幅值和相位均增加了。在這樣的控制器下,校正后系統的相位裕量增加到 處系統的幅值和相位均增加了。在這樣的控制器下,校正后系統的相位裕量增加到 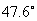 ,而剪切頻率增加到 ,而剪切頻率增加到 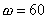 。 。
(4) 繪制校正后系統的Bode圖如圖6-18a中的實線所示。用如下的Matlab語句繪制校正前后系統的階躍響應曲線如圖6-18c。
[m,p]=bode(G0,w);[m1,p1]=bode(G_o,w);
subplot(211),semilogx(w,20*log10([m(:),m1(:)]))
subplot(212),semilogx(w,[p(:),p1(:)])
G_c1=feedback(G0,1);G_c2=feedback(G_o,1);
[y,t]=step(G_c1);y=[y,step(G_c2,t)];
figure,plot(t,y)
|  電子發燒友App
電子發燒友App

 硬聲App
硬聲App

 1827
1827 884
884 2258
2258 2593
2593 840
840 2767
2767
 2788
2788 6
6 4
4 603
603 2
2 10
10 9066
9066 87525
87525 55
55 1
1 51
51 60
60 305
305 53
53
 69
69 1984
1984
 359
359 837
837
 1741
1741
評論