|
與頻域法相似,利用根軌跡法進行系統的設計也有兩種方法:1)常規方法;2)Matlab方法。Matlab的根軌跡方法允許進行可視化設計,具有操作簡單、界面直觀、交互性好、設計效率高等優點。目前常用的Matlab設計方法有:1)直接編程法;2)Matlab控制工具箱提供的強大的Rltool工具;3)第三方提供的應用程序,如CTRLLAB等。本節在給出根軌跡的設計思路的基礎上,將重點介紹第一、二種方法。
6.4.1 超前校正
關于超前校正裝置的用途,在頻率校正法中已進行了較詳細的敘述,在此不再重復。
利用根軌跡法對系統進行超前校正的基本前提是:假設校正后的控制系統有一對閉環主導極點,這樣系統的動態性能就可以近似地用這對主導極點所描述的二階系統來表征。因此在設計校正裝置之前,必須先把系統時域性能的指標轉化為一對希望的閉環主導極點。通過校正裝置的引入,使校正后的系統工作在這對希望的閉環主導極點處,而閉環系統的其它極點或靠近某一個閉環零點,或遠離s平面的虛軸,使它們對校正后系統動態性能的影響最小。
是否采用超前校正可以按如下方法進行簡單判斷:若希望的閉環主導極點位于校正前系統根軌跡的左方時,宜用超前校正,即利用超前校正網絡產生的相位超前角,使校正前系統的根軌跡向左傾斜,并通過希望的閉環主導極點。 (一)根軌跡超前校正原理
設一個單位反饋系統,G0(s)為系統的不變部分,Gc(s)為待設計的超前校正裝置,
Kc為附加放大器的增益。繪制G0(s)的根軌跡于圖6—19上,設點Sd 為系統希望的閉環極點,則 若為校正后系統根軌跡上的一點,必須滿足根軌跡的相角條件,即
∠Gc(Sd)G0(Sd)=∠Gc(Sd)+G0(Sd)=-π
于是得超前校正裝置提供的超前角為:
顯然在Sd已知的情況下,這樣的Gc(s)是存在的,但它的零點和極點的組合并不唯一,這相當于張開一定角度的剪刀,以Sd為中心在擺動。若確定了Zc和Pc的位置,即確定了校正裝置的參數。下面介紹三種用于確定超前校正網絡零點和極點的方法。
(二)三種確定超前校正裝置參數的方法
零極點抵消法
在控制工程實踐中,通常把Gc(s)的零點設置在正對希望閉環極點Sd下方的負實軸上,或位于緊靠坐標原點的兩個實極點的左方,此法一般可使校正后系統的期望閉環極點成為主導極點。
比值α最大化法
能使超前校正網絡零點和極點的比值α為最大的設計方法。按照該法去設計Gc(s)的零點和極點,能使附加放大器的增益盡可能地小。
以圖6—19上的點O和Sd,以Sd為頂點,線段O 為邊,向左作角γ,角γ的另一邊與負實軸的交點Zc=-1/T,點Zc就是所求 的一個零點。再以線段ZcSd為邊,向左作角
∠PcSdZc,該角的另一邊與負實軸的交點Pc=-1/αT,點 就是所求Gc(s)的一個極點。根據正弦定理,由圖6—18求得:
于是有:
將夾角γ作為自變量,式(6—24)對γ求導,并令其等于零,即dα/dγ=0
由上式解得對應于最大α值時的γ角為
不難看出,當希望的閉環極點Sd被確定后,式(6—25)中的θ和φ均為已知值,因而由上式可求得γ角,然后由式(6-22)和式(6-23)求得相應的零極點。
幅值確定法
設系統的開環傳遞函數:
且令超前校正裝置的傳遞函數:
若要求校正后系統的穩態誤差系數K(Kp,Kv,Ka),則由上式可首先確定k:
在開環增益k確定后,根據根軌跡原理,若Sd為校正后的閉環極點,則它除必須滿足相角條件外,還應滿足幅值條件:
| 上式中, |
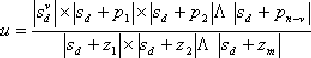 |
同樣根據平面三角形原理,對于△ZcOSd有:
而對于△PcOSd有:
由上二式消去sinθ,并由式(6-29)可得:
根據三角函數性質,上式可寫成如下形式:
進而有:
由于k可由穩態誤差系數確定,u由未校正傳遞函數求出,因此根據上式求出角γ。最后可用式(6-22)和式(6-23)確定校正裝置的零極點和具體參數。
通過上述分析可知,對于超前校正裝置的參數確定,可用三種方法進行設計,其中第一法是工程經驗方法,第二法則是從抑制高頻噪聲角度出發進行設計,第三法則先在滿足靜態性能指標的條件下設計滿足動態性能指標的控制器。但必須指出,上述三法均用于對靜態性能要求不高而系統的動態性能需要改善的控制系統,校正后的系統應滿足根軌跡的相角條件和幅值條件。若系統的靜態性能指標較高,可能無法設計合適的超前校正裝置,此時應采用遲后-超前校正裝置。
(三)根軌跡超前校正的步驟
綜上所述,用根據軌跡法進行超前校正的一般步驟為:
1)根據對系統靜態性能指標和動態性能指標的要求,分析確定希望的開環增益k閉環主導極點Sd的位置.
2)畫出校正前系統的根軌跡,判斷希望的主導極點位于原系統的根軌跡左側,以確定是否應加超前校正裝置。
3)根據式(6—21)解出超前校正網絡在Sd點處應提供的相位超前角φ。
4)選擇前面介紹的三種方法之一,求γ,爾后用圖解法或根據式(6—22)和式(6—23)求得Gc(s)的零點和極點,進而求出校正裝置的參數。
5)畫出校正后系統的根軌跡,校核閉環主導極點是否符合設計要求。
6)若采用第一法和第二法,則還須根據根軌跡的幅值條件,確定校正后系統工作在 處的增益和靜態誤差系數。如果所求的靜態誤差系數與要求的值相差不大,則可通過適當調整Gc(s)零點和極點的位置來解決;如果所求的靜態誤差系數比要求的值小得多,則需考慮用別的校正方法,如用遲后—超前校正。
下面舉例分別介紹上述三法的使用,進而對根軌跡超前校正步驟進行說明。
例6-5 已知一單位反饋控制系統的開環傳遞函數為:
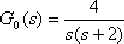
試設計一超前校正裝置,使校正后系統的無阻尼自然頻率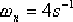 ,阻尼比 ,阻尼比 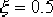 。 。
解:(1)這是一個積分環節和慣性環節串聯的系統,系統的無阻尼自然頻率 ,阻尼比 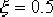 ,閉環極點為 以及靜態速度誤差系數 ,閉環極點為 以及靜態速度誤差系數 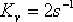 ,校正前系統的根軌跡如圖6—20虛線所示。 ,校正前系統的根軌跡如圖6—20虛線所示。
(2)由 和 和 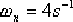 ,求得希望的閉環極點為: ,求得希望的閉環極點為:
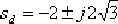 。 。
(3)計算超前校正裝置在 處需提供的相位超前角。由于未校正系統的 在 在 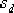 處的相角為: 處的相角為:
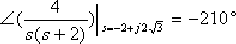
為了使校正后系統的概軌跡能通過希望的極點,超前校正裝置必須在該點產生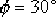 的超前角。 的超前角。
(4)根據根軌跡的相角條件,確定超前校正裝置的零點和極點。因為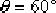 , , 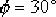 ,所以 ,所以 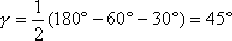 。按照最大α值的設計方法,可計算或作圖求出 。按照最大α值的設計方法,可計算或作圖求出  , , 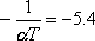 。這一校正裝置的傳遞函數 。這一校正裝置的傳遞函數 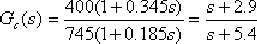 。于是求得由校正網絡和附加放大器組成的超前校正裝置的傳遞函數,并得到校正后系統的開環傳遞函 。于是求得由校正網絡和附加放大器組成的超前校正裝置的傳遞函數,并得到校正后系統的開環傳遞函
數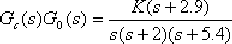
式中,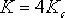 。由上式作出校正后系統的根軌跡,如圖6—20中的實線所示。 。由上式作出校正后系統的根軌跡,如圖6—20中的實線所示。
(5)確定系統工作在希望閉環極點處的增益和靜態速度誤差系數。由根軌跡的幅值條件
解得 。由于 。由于  ,因而 ,因而 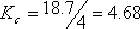 。系統對應的開環傳遞函數為 。系統對應的開環傳遞函數為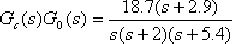
由上式求得校正后系統的靜態速度誤差系數
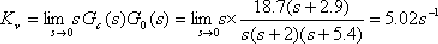
校正后系統的閉環傳遞函數可由Matlab中的G=feedback(Gc*G,1)得到:

由上式可見,校正后的系統雖上升為三階系統,但由于所增加的一個閉環極點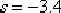 與其零點 與其零點 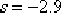 靠得很近,因而這個極點對系統瞬態響應的影響就很小,從而說明了 靠得很近,因而這個極點對系統瞬態響應的影響就很小,從而說明了  確為系統一對希望的閉環主導極點。由于本例題對系統的靜態誤差系數沒有提出具體的要求,故認為上述的設計是成功的。 確為系統一對希望的閉環主導極點。由于本例題對系統的靜態誤差系數沒有提出具體的要求,故認為上述的設計是成功的。
例6-6 設一單位反饋控制系統的開環傳遞函數為
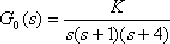
試設計一超前校正裝置,使校正后的系統能具有下列的性能指標:超調量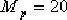 %,調整時間 %,調整時間 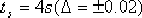 。 。
解:(1)作出校正前系統的根軌跡,如圖6—21所示。
(2)根據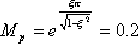 ,解得 ,解得 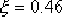 ,考慮到非主導極點和零點對超調量的影響,取 ,考慮到非主導極點和零點對超調量的影響,取 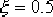 。又由 。又由 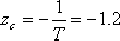 ,求得 ,求得  。進而求得系統的一對希望的閉環主導極點 。進而求得系統的一對希望的閉環主導極點 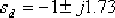 。 。
(3)根據求得的主導極點,計算超前校正網絡在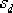 處應提供的超前角為 處應提供的超前角為
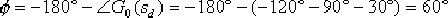
(4)由于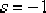 的開環極點正好落在希望閉環極點 的開環極點正好落在希望閉環極點 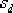 下方的負實軸上,因此可采用第一法進行校正。把 下方的負實軸上,因此可采用第一法進行校正。把 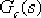 的零點設置在緊靠 的零點設置在緊靠  這個開環極點的左側。如設 這個開環極點的左側。如設 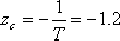 ,則 ,則 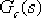 的極點落在以 的極點落在以 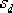 為頂點,向左作角 為頂點,向左作角  的負實軸交點上, 的負實軸交點上, 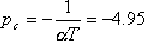 ,即為所求 ,即為所求  的極點。 的極點。
(5) 校正后系統的傳遞函數為
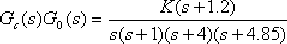
由根軌跡的幅值條件,求得系統工作于 點處的K值為30.4。這樣,上式便改寫為
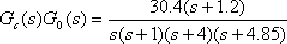
據此,求得校正后系統的靜態速度誤差系數
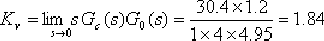
如果希望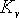 值有少量地增大,則可通過適當調整 值有少量地增大,則可通過適當調整 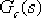 零點和極點的位置來實現,但這種調整有可能會破壞 的主導作用。 零點和極點的位置來實現,但這種調整有可能會破壞 的主導作用。
(6)它的閉環傳遞函數為:
或直接由如下的Matlab命令得到:
zpk(feedback(G0*Gc,30.4))
Zero/pole/gain:
(s+1.2)
------------------------------------------
(s+6.631) (s+1.347) (s^2 + 1.972s + 4.085)
下面檢驗希望閉環極點 是否符合主導極點的條件。不難看出,由于閉環系統的一個極點與零點靠得很近,故它對系統瞬態響應的影響很小,同時由于另一極點 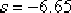 距s平面的虛軸較遠,因而這個瞬態分量不僅幅值小,而且衰減的速度也快。由此得出,上述設計的超前校正裝置能使 成為系統希望的閉環主導極點。 距s平面的虛軸較遠,因而這個瞬態分量不僅幅值小,而且衰減的速度也快。由此得出,上述設計的超前校正裝置能使 成為系統希望的閉環主導極點。
上面兩個例題均對靜態誤差系數沒有特殊要求,否則,宜采用如下方法,即第三法。
例6-7 有一單位反饋系統,其開環傳遞函數: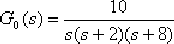 ,設計一超前校正裝置,滿足如下性能指標:靜態誤差系數 ,設計一超前校正裝置,滿足如下性能指標:靜態誤差系數  ,閉環主導極點位于: ,閉環主導極點位于: 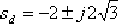 處。 處。
解:(1)繪制未校正系統的根軌跡,并根據靜態誤差系統,確定開環增益:
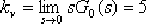 , ,  , ,
(2)根據幅值確定法,并代入:
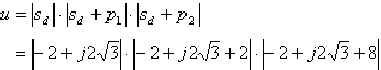
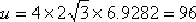
超前校正裝置應提供的超前角度:
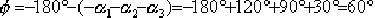
(3)根據公式(6-34)確定夾角 γ:

得到:
(4)由設計要求, , , ,求出校正裝置的參數。
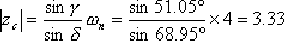 , ,
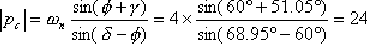 , ,
得到: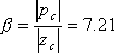 , , 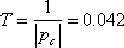 。因而超前校正裝置的傳遞函數: 。因而超前校正裝置的傳遞函數: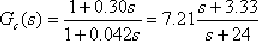
(5)校正后閉環系統的傳遞函數和主導極點分別為:
G=G0*Gc
Transfer function:
576.8 s + 1921
------------------------------
s^4 + 34 s^3 + 256 s^2 + 384 s
Gl=feedback(G0*Gc,1)
zpk(Gl)
Zero/pole/gain:
576.8 (s+3.33)
------------------------------------------
(s+25.25) (s+4.745) (s^2 + 4.006s + 16.03)
顯然,系統靜態誤差系數為: ,主導極點為: ,設計基本符合要求。
6.4.2 遲后校正
通過設置校正裝置的零極點,使之形成一對在S平面上靠近原點的偶極子,這樣,在基本保持原系統主導極點的前提下,可提高系統的靜態誤差系數而不致使系統的動態性能變壞。
例如,對于一單位反饋系統,若其開環傳遞函數:G0(S)=K/s(s+a)(s+b),則靜態速度誤差系數Kv=K/ab ,因為系統主導極點為Sd,則K=|Sd|·|Sd+a|·|Sd+b|。串聯遲后校正裝置后,開環傳遞函數:
若要求主導極點基本不變,則
由于設計時選取的-1/τ和-1/βτ均靠近原點,因此
可見校正后靜態誤差系數增大了約β倍,而主導極點可基本保持不變。
由上,可得出遲后校正的根軌跡法步驟:
(1)畫出未校正開環系統的根軌跡;
(2)根據系統設計的時域指標,確定主導極點Sd,進而計算未校正系統的增益K及靜態誤差系數Kv ;
(3)將要求的靜態誤差系統與未校正系統的靜態誤差系數進行比較;得出遲后校正裝置的β值;
(4)確定校正裝置的零點和極點。零點的確定方法是:以主導極點Sd為頂點,引線為起起始邊,向左旋轉5°-10° ,此邊與負實軸的交點即為校正裝置的零點-1/τ ,由(3)中β值進而確定校正裝置極點-1/βτ。
(5)畫出校正后系統的根軌跡。若新的主導極點Sd1或靜態誤差系數與設計要求相關較大,則宜適當調整β或-1/υ ,直至滿足要求。
需要說明的是,上述推導過程中按Kv 進行說明,但對于Kp或Ka結論相似。
例6-8 已知一單位反饋控制系統的開環傳遞函數為
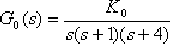
要求校正后的系統能滿足下列的性能指標:阻尼比ξ=0.5 ;調整時間ts=10s;靜態速度誤差系數Kv≥5/s。解:(1)繪制未校正系統的根軌跡如圖6—23中的虛線所示。
(2)根據給定的性能指標,確定系統的無阻尼自然頻率為

據此,求得希望的閉環主導極點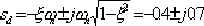
(3)由根軌跡的幅值條件,確定未校正系統在 處的增益,即根據 ,求得 ,,相應的靜態速度誤差系數為
(4)基于校正后的系統要求,據此算出遲后校正裝置的參數β值,即
考慮到遲后校正裝置在 點處產生遲后角的影響,所選取的β值應大于7.5,現取β=10。
(5)由點 作一條與線段O 成 角的直線,此直線與負實軸的交點就是校正裝置的零點,由圖6—23 可知,零點 ,極點為 。這樣,校正裝置的傳遞函數
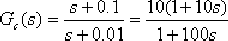
校正后系統的開環傳遞函數
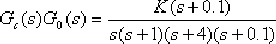
校正后系統的根軌跡如圖6—23中的實線所示。由該圖可見,若要使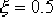 ,則校正后系統主導極點的位置略偏離要求值,即由 點移到 ,則校正后系統主導極點的位置略偏離要求值,即由 點移到 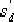 點。相應的增益 點。相應的增益  。 。
校正后系統的開環傳遞函數為
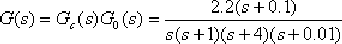
相應的靜態速度誤差系數為: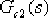 。 。
比較未校正系統和校正后系統的根軌跡可見,校正后系統的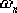 從0.8減到0.7,這意味著調整時間略有增加。如果對此不滿意,則可重新選擇希望閉環主導極點的位置,且使其 從0.8減到0.7,這意味著調整時間略有增加。如果對此不滿意,則可重新選擇希望閉環主導極點的位置,且使其 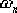 值略高于0.8。 值略高于0.8。
6.4.3 遲后—超前校正
由上兩節的討論可知,超前校正主要用于提高系統的穩定裕度,改善系統的動態性能,而遲后校正則可以減少系統的穩態誤差。由此設想,若把這兩種校正結合起來應用,必然會同時改善系統的動態和靜態性能,這就是遲后—超前校正的基本思路。
當希望的閉環主導極點Sd位于未校正系統根軌跡的左方時,如只用單個超前網絡對系統進行校正,雖然也能使校正后系統的根軌跡通過Sd點,但無法使系統在該點具有較大的開環增益,以滿足靜態性能的需要。對于這種情況,一般宜采用遲后—超前校正。
設遲后—超前校正裝置的傳遞函數為
其中Gc1(s)起遲后校正作用,它使系統在Sd處的開環增益有較大幅度的增大,以滿足靜態性能的需要;Gc2(s)起超前校正作用,利用它所產生的相位超前角φc2使根軌跡向左傾斜,并通過希望的閉環主導極點Sd,從而改善系統的動態性能。
用根軌跡法進行遲后—超前校正的一般步驟為:
1)根據對系統性能指標的要求,確定希望閉環主導極點Sd的位置。
2)設計校正裝置的超前部分Gc2(s)。設計時要兼顧到既使Gc2(s)在Sd處產生的相位超前角φc2滿足Sd點的相角條件,又使Gc2(s)極點與零點的比值β足夠大,以滿足遲后部分使系統在Sd點的開環增益有較大幅度增大的需要。
3)根據所確定的β值,按遲后校正的設計方法去設計Gc1(s)。
4)畫出校正后系統的根軌跡。由根軌跡的幅值條件,計算系統工作在Sd處的靜態誤差系數。如果所求的值小于給定值,則需增大β值,應從步驟2)開始重新設計。
下面以實例說明這種校正的具體步驟。
例6—9 校正前該系統的開環傳遞函數為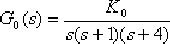
要求校正后具有下列的性能指標:阻尼比 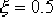 ;無阻尼自然頻率 ;無阻尼自然頻率 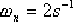 ;靜態速度誤差系數 ;靜態速度誤差系數 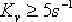 。試設計一遲后—超前校正裝置。 。試設計一遲后—超前校正裝置。
解(1)根據給定的性能指標,求出希望的閉環主導極點為
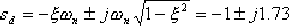
(2)設計校正裝置。超前部分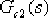 在 在 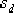 處應提供的超前角 處應提供的超前角
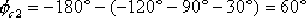
令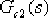 的零點 的零點 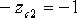 ,以抵消原系統的一個開環極點。這樣設計不僅使校正后系統的階數降低,繪制根軌跡方便,而且一般易于實現希望閉環極點的主導作用。在圖6-24所示的s平面上,以 ,以抵消原系統的一個開環極點。這樣設計不僅使校正后系統的階數降低,繪制根軌跡方便,而且一般易于實現希望閉環極點的主導作用。在圖6-24所示的s平面上,以 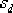 點為頂點,點 點為頂點,點 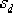 與-1點的連線為邊,向左作角 與-1點的連線為邊,向左作角  ,該角的另一邊與負實軸的交點 ,該角的另一邊與負實軸的交點  ,這就是所求超前部分的極點。由此可見, ,這就是所求超前部分的極點。由此可見, 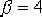 , ,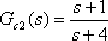 。 。
(3)經過超前部分校正后,系統的傳遞函數為
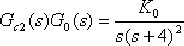
據此,作出相應的根軌跡,如圖6-24中的實線所示。根據根軌跡的幅值條件,求得系統工作在 點時的增益 點時的增益 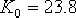 ,對應的靜態速度誤差系數為 ,對應的靜態速度誤差系數為

顯然,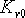 不能滿足給定指標的要求,所要增大的倍數 不能滿足給定指標的要求,所要增大的倍數 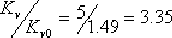 應由遲后部分 應由遲后部分 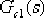 來提供。由此可見,上述確定的β=4能滿足將靜態速度誤差系數提高3.35倍的要求。 來提供。由此可見,上述確定的β=4能滿足將靜態速度誤差系數提高3.35倍的要求。
(4)設計校正裝置的遲后部分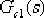 。 。
由點 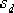 向左作一條與線段 向左作一條與線段  成 成 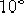 角的直線,此直線與負實軸交于 角的直線,此直線與負實軸交于 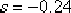 ,這就是所求 的零點,它的極點 ,這就是所求 的零點,它的極點 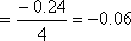 。于是求得遲后部分的傳遞數為 。于是求得遲后部分的傳遞數為
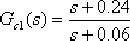
經遲后—超前校正后,系統的開環傳遞函數為
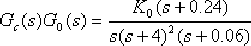
校正后系統的根軌跡如圖6-24中的虛線所示。由圖可見,校正后系統的主導極點由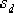 點移動到 點移動到 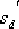 點,相應的增益 點,相應的增益  ,靜態速度誤差系數為 ,靜態速度誤差系數為

利用Matlab進行串聯校正設計步驟,以例6-9為例,要求校正后具有下列的性能指標:阻尼比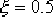 ;無阻尼自然頻率 ,但對靜態誤差系統沒有要求。可按如下步驟進行: ;無阻尼自然頻率 ,但對靜態誤差系統沒有要求。可按如下步驟進行:
(1) 寫出系統傳遞函數G,并畫出其根軌跡。
G0=tf(1,conv([1,1],[1,4]),0);
Rlocus(G0);hold on;[x,y]=rloc_asymp(G0);plot(x,y,’:’)
(1)根據設計要求,畫出其等ξ線和等ωn線,并由圖確定其主導極點。
Zet=[0.5];wn=[2];sgrid(zet,wn)
由圖可得到sd=-1±1.732j
(2)確定超前裝置的補償角φc,利用自編函數angle_c計算。
Fi_c=angle_c(G0,sd)
(3)確定校正器的零極點。可先選定校正器的零點zc=-1.2,然后由已知的γ、ωn、θ、φc計算極點。
Pc=find_pc(wn,zc,theta,fi_c)
(4)得到校正裝置Gc,并畫出Gc*G0的根軌跡圖。
Hold on; Rlocus(Gc*G0)
(5)從圖中交互確定在sd處對象的K值,并進而得出系統的閉環極點及階躍響應。檢驗設計效果。
[K,P]=rloc_find(Gc*G0)。
此例完整程序見下面,設計效果見圖6-25。
G0=tf(1,[conv([1,1],[1,4]),0])
Transfer function:
1
-----------------
s^3 + 5 s^2 + 4 s
Rlocus(G0);hold on;[x,y]=rloc_asymp(G0);plot(x,y,':')
zet=[0.5];wn=[2];sgrid(zet,wn)
sd=-1+1.732j;
Fi_c=angle_c(G0,sd)
Fi_c =
60.0000
Fi_c=Fi_c*pi/180;
zc=-1.2;theta=acos(0.5);
pc=find_pc(wn,zc,theta,Fi_c);
pc =
5.0000
Gc=tf([1,-zc],[1,pc])
Transfer function:
s + 1.2
-------
s + 5
Hold on; Rlocus(Gc*G0)
[K,P]=rlocfind(Gc*G0)
Select a point in the graphics window
selected_point =
-1.0001 + 1.7315i
K =
29.9894
P =
-6.6454
-1.0001 + 1.7315i
-1.0001 - 1.7315i
-1.3543
function ang=angle_c(g,sd)
[p,z]=pzmap(g);
theta_z=0;theta_p=0;
for i=[1:1:length(z)]
theta_z=theta_z+angle(sd-z(i));
end
for i=[1:1:length(p)]
theta_p=theta_p+angle(sd-p(i));
end
ang=(-pi+theta_p-theta_z)*180/pi;end
function pc=find_pc(wn,zc,theta,fc)
gama=atan(sin(theta)/(wn/abs(zc)-cos(theta)));
pc=wn*sin(gama+fc)/sin(pi-theta-fc-gama)
6.4.4基于根軌跡的串聯校正Matlab設計
在采用根軌跡法對控制系統進行校正時,常用的函數有:
1.Rlocus: 根軌跡作圖命令;
2.Sgrid: 等ξ線和等ωn線;
3.Tf、Zpk: 求傳遞函數命令;
4.Rlocfind: 求取根軌跡上某點對應的增益K及閉環極點;
5.Rloc_asymp: 作軌跡漸近線;
6.Rltool: 由Matlab提供的根軌跡設計工具;
7.Pzmap,pole,zer 求取系統的零極點。
利用Matlab進行串聯校正設計有兩種方法:一種是利用書中介紹的步驟進行設計,另外也可以用Matlab提供的rltool可視化工具進行交互式設計。 |  電子發燒友App
電子發燒友App

 硬聲App
硬聲App

 1827
1827 884
884 2258
2258 2593
2593 840
840 2767
2767
 2788
2788 6
6 4
4 603
603 9066
9066 22
22 87525
87525 55
55 1
1 51
51 60
60 305
305 53
53
 69
69 1984
1984
 359
359 837
837
 1741
1741
 7
7
評論