前言

第一篇博客就從運放入手吧，話不多說。正文開始：想必大家對運放電路都熟悉的再不能熟悉了。可是這里為什么又再拿出來寫呢?肯定是有不同的知識才會有意義，所以接下來就本人在積累到的前人的知識，拿出來淺談淺談，不當之處希望大家指正。

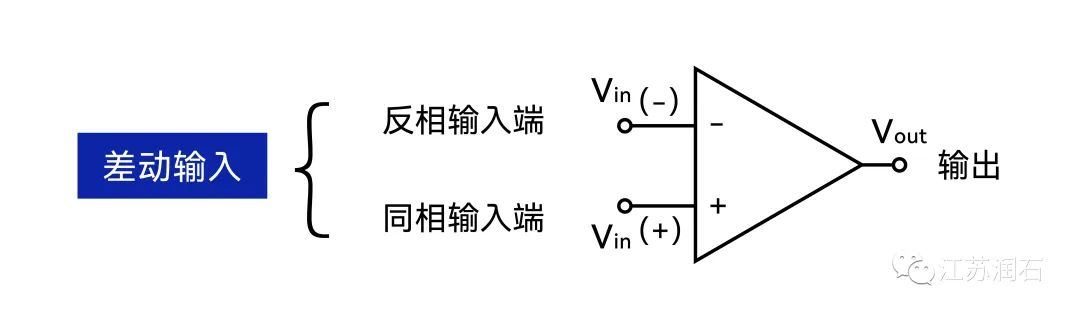
四種基本的運算放大電路

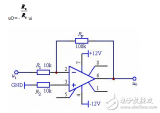
1. 同相放大電路

?

?

?

?

?

?

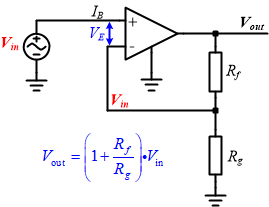
同相放大電路：顧名思義輸出和輸出信號是相位相同。放大倍數由Rg和Rf共同決定。

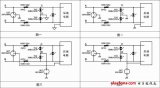
2. 反向放大電路

?

?

?

?

?

?

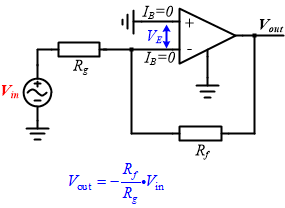
反相放大電路：顧名思義輸出和輸出信號是相位相反。放大倍數由Rg和Rf共同決定。

3.加法器

?

?

?

?

?

?

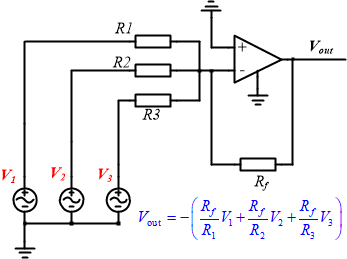
加法器：顧名思義輸出是輸入信號的和。每個信號的放大倍數有反饋電阻Rf與每個輸入信號串聯的電阻R共同決定。

4. 差分放大電路

?

?

?

?

?

?

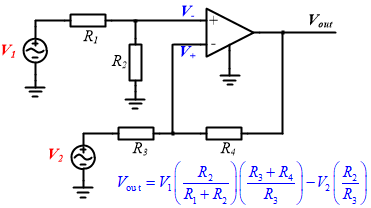
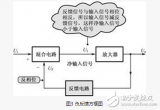
差分放大電路：輸出信號是輸入信號之差。輸出信號可先由分壓器規則計算同相輸入端的電壓V+，然后使用同相運放增益公式計算出通相輸出電壓Vout1。然后在使用反向增益公式計算反向輸出級的電壓Vout2。最后將兩個輸出電壓相加即可。

到此為止是屬于大家在都熟知的基本知識。

以上都是基于理想運算放大器設計，然而，由于運放的開環響應，會出現一些很小但應當注意的誤差項。例如反相放大器的增益是否永遠都能夠由-Rf/Rg決定，同相放大器的增益是否由1+Rf/Rg決定?答案是，但也不是。這就要考慮到運放的開環增益，理想的開環增益無窮大，那么誤差項為0;當開環增益遠遠大于預期的閉環增益時，那么誤差項的值也會小到去可在設計中忽略。但是，當閉環增益增大時，誤差項這時候就不可能被忽略掉了，如果被忽略，設計出來的電路的增益就會和理論設計的相違背。

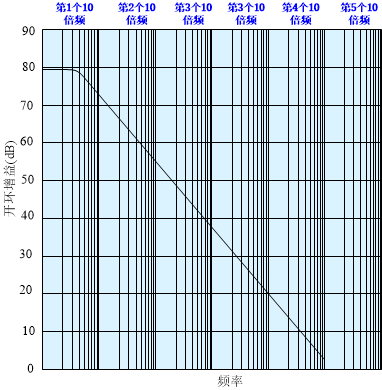
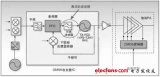
接下來先介紹一個常見的運放的開環響應，如下圖所示。很多人一眼望去，這圖好熟悉呀。That’s right!這和簡單的低通濾波器的幅頻響應曲線圖一樣

?

?

?

?

?

?

這一曲線主要包括兩段：一段是水平的，一段是傾斜的。最左邊的頻率，開環增益為80dB(即10 000V/V)。所以這一頻率下能夠達到的最大增益為10000。只要頻率增加3個十倍頻程，這一情況就會發生顯著改變來響應曲線開始傾斜，能達到的最大增益只有小于40dB，或者小于100V/V。由此可知，在這一頻率下運放能夠獲得的最大增益就顯著被限制了。

考慮到開環增益的影響，單級反相放大和同相放大運放電路在實際中的增益由一下兩條公式給出。

?

?

?

?

?

?

?

?

?

?

?

?

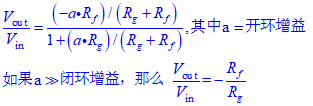
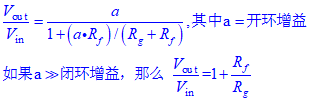
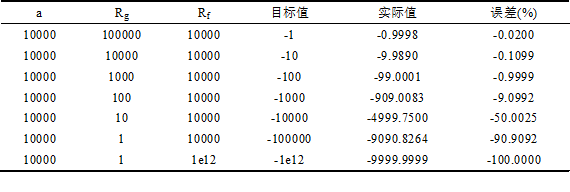
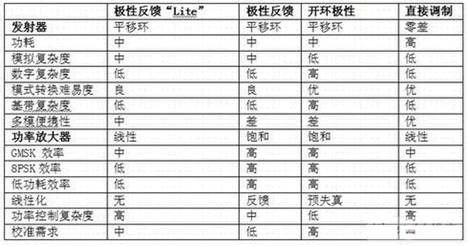
考慮到上圖的開環響應圖，假設頻率足夠低，開環增益為80dB，即能夠達到的最大增益為10000.有限開環增益對反向放大電路實際增益的影響如下表所示

?

?

?

?

?

?

當Rf=Rg，理論增益為-1，有限開環增益只貢獻了0.02%的誤差。因此，使用誤差為1%的電阻時，電阻誤差都比這個誤差還要大，因此，這個由開環增益引起的0.02%的誤差便可以忽略不計了。但是當增益為-100時，誤差達到了1%，這就足夠引起注意了。略微調整電阻的值可以補償這一誤差。然而當理論增益增大到10000時，誤差也增加到了50%，無論如何調整都無法補償。如果使用一些阻值懸殊的電阻。如Rg=1Ω，Rf=1TΩ，那么能夠達到的最大增益的絕對值仍然達不到10000。就像光速一樣，你能夠無限接近它，然是永遠達不到。

同理，對于同相放大電路，其實際增益與理論增益由下表所示。低增益時誤差可忽略，或者微調電阻值便可以誤差范圍內滿足設計。但是誤差達到50%，通過調整電阻值，取一些荒謬的阻值來達到增益要求，可以接近但是永遠無法達到開環增益。

后面這些內容似乎難懂，與實際也比較不沾邊，與所學的相差甚遠。但是，在設計放大器電路時，我們應該講這些牢記于心，因為這才是運放的真正性質。

再往后的有源濾波器設計講解中，也會受到類似的限制，一條很有用的經驗法則是(不是本人得出來的，從前人那里積累的)：在最高的工作頻率上確保開環增益比所需增益打40dB，否則可能會出現誤差，對于帶通濾波器的情形，這種的限制還會使諧振頻率降低。